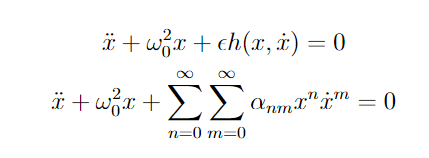Table of Contents
Nonlinear dynamics analysis python tool. Features include phase plots, duffing system, bifurcation, nonlinear approximation methods, etc.
This project is based on nonlinear dynamics and analysis referenced mainly from Nayfeh and Mook. The goal of this project is to provide a strong set of tools to analyze nonlinear dynamical systems using techniques and theories such as
- Hamilton's principle
- Discretization techniques
- Phase plane analysis
- Local stability analysis of (nonlinear) equilibria (fixed points)
- Bifurcation analysis of fixed points
- Weakly nonlinear oscillations and perturbation analysis
- Conservative systems
- Nonconservative systems - damped and forced
- Parametrically excited systems
- Averaging
- Lindstedt-Poincare
- Multiple Scales
- Harmonic Balance
- Floquet Theory
- Homotopy Techniques
- Quasiperiodic solutions
- Poincare sections and maps
- Introduction to chaos and fractals
- Classical routes to chaos
- Installing Anaconda from here and Git from here.
- Create a new conda environment with required packages (will not setup from a .txt or .yml file to avoid conflicts occurring from the use of different OS).
conda create --name pythononlinear python>=3.8 numpy pandas matplotlib sympy jupyter jupyterlab
- Activate the new environment and add packages you might want to have.
conda activate pythononlinear
conda install -c conda-forge control
- Clone this repository to your desired location.
git clone https://github.com/smallpondtom/pNLsys.git
- Navigate to the notebook directory inside pNLsys and open up Jupyter Lab.
cd pNLsys/notebooks
jupyter lab
- Alternatively you can just download the Jupyter notebook files and open them with Google Colaboratory which is a free Jupyter lab like platform where you can code and execute Python. Learn more.
You can simply run the Jupyter notebooks and see the demonstrations of nonlinear dynamics done in Python language.
For Georgia Institute of Technology students, you are more than welcome to use this project for your studies and improve upon it. Especially if you are taking the Mechanical Engineering Course ME6444 Nonlinear Systems.
Furthermore, it would be heavily appreciated if you could point out mathematical or even theoretical mistakes in this repository so that I can fix them. Or if you would like, you can go ahead and fork this repository and fix it yourself. Once you do you can create a pull request as noted in the Contributing section.
Currently, I am working to create a python library called pNLsys based on the
Jupyter notebooks in this repository.
-
One great feature to add to this project is expanding the
DEplotfunction to a more general use case. Currently, this function only supports second order, single variable ODEs and cannot plot the phase plane for multivariate higher order differential equations. -
Another improvement would be to create a new function which approximates the nonlinear parametrically excited system using the methods covered in the notebooks such as averaging, Lindstedt-Poincare, etc. This function would take an input which could be any general kind of excited system in the form shown below (also the Taylor expanded form). The function will perform an approximation indicated by another function argument using Sympy and return the approximated equation.
- Pertaining to chaotic systems, it would be ambitious to create a python library that specializes in chaotic system identification and its analysis using the techniques studied in the ME6444 (course at Georgia Tech) as well as other effective theories and techniques.
See the open issues for a list of proposed features (and known issues).
- Top Feature Requests (Add your votes using the 👍 reaction)
- Top Bugs (Add your votes using the 👍 reaction)
- Newest Bugs
Please reach out to:
- GitHub issues
- Contact options listed on this GitHub profile
If you want to say thank you or/and support active development of pNLsys:
- Add a GitHub Star to the project.
- Write interesting articles about the project on Dev.to, Medium or your personal blog.
Together, we can make pNLsys better!
If you would like to contribute to this project please go ahead and fork this project and create a pull request to the original repository. I will be actively monitoring this project and will incorporate any great new improvements from motivated folks.
Please read our contribution guidelines. I appreciate the contribution.
The original setup of this repository is by Tomoki Koike a Georgia Tech AE graduate student.
For a full list of all authors and contributors, see the contributors page.
This project is licensed under the MIT license.
See LICENSE for more information.
[1] Dr. Micheal Joseph Leamy, ME6444, Georgia Institute of Technology.
[2] Nayfeh and Mook, 2004, Nonlinear Oscillation.
[3] Nayfeh and Balachandran, 2004, Applied Nonlinear Dynamics.
[4] Stephen Lynch, 2001, Dynamical Systems with Applications Using Maple.