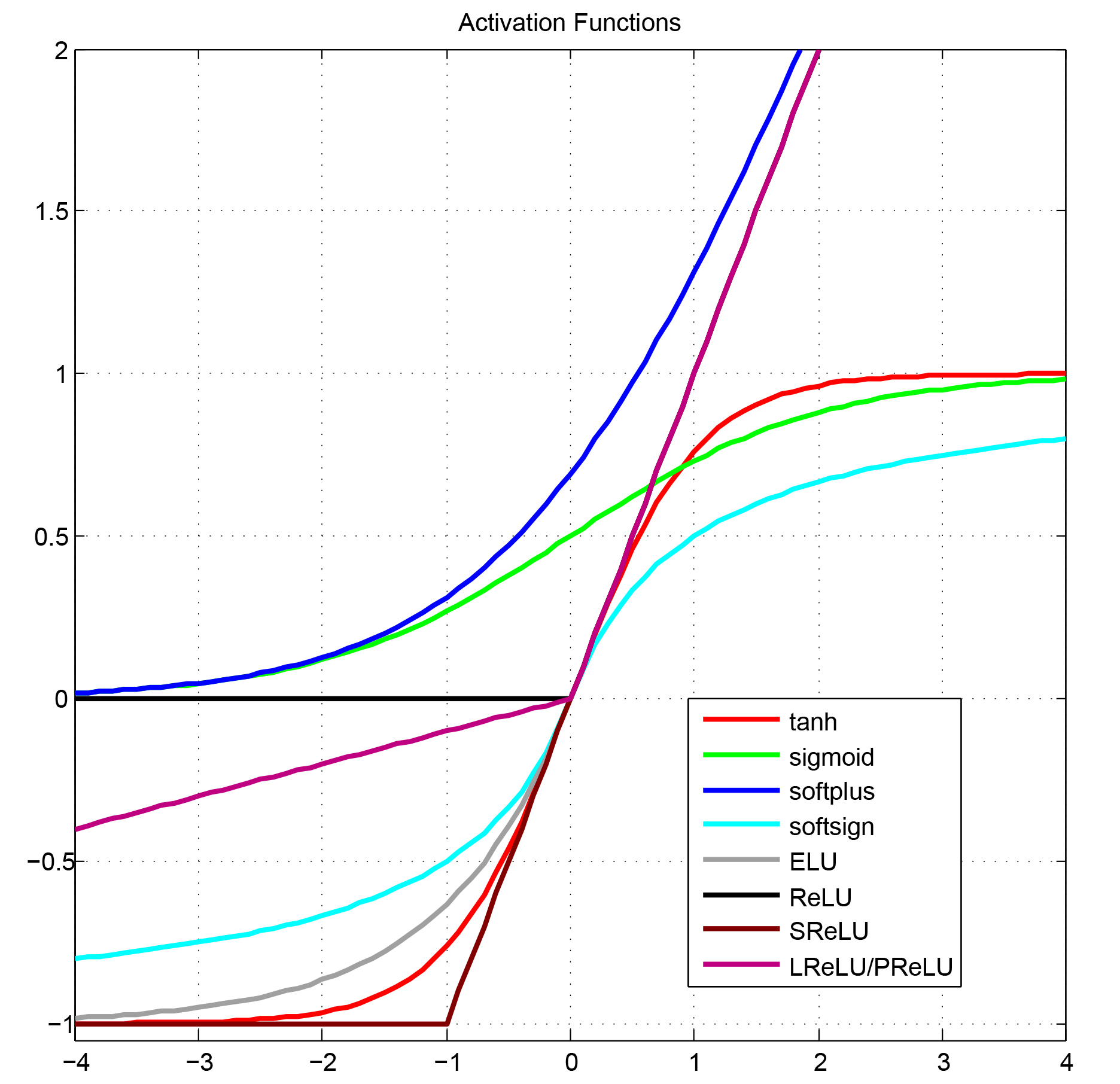
##Activation Functions
简单整理了一下目前深度学习中提出的激活函数,按照激活函数是否可微的性质分为3类:
-
平滑非线性函数(Smooth nonlinearities):
-
tanh : Efficient BackProb, Neural Networks 1998
$$f(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}$$ -
sigmoid: Efficient BackProb, Neural Networks 1998
$$f(x) = \frac{1}{1+e^{-x}}$$ -
softplus: Incorporating Second-Order Functional Knowledge for Better Option Pricing, NIPS 2001
$$f(x) = ln(1+e^x)$$ -
softsign:
$$f(x) = \frac{x}{|x| + 1}$$ -
ELU: Fast and Accuracy Deep Network Learning by Exponential Linear Units, ICLR 2016 $$f(x)= \begin{cases} \begin{array}{lcl} x & & ; x>0 \ \alpha(e^x - 1) & & ; x \leq 0, \alpha = 1.0 \ \end{array} \end{cases}$$
-
连续但并不是处处可微(Continuous but not everywhere differentiable)
-
ReLU: Deep Sparse Rectifier Neural Networks, AISTATS 2011
$$f(x) = max(0, x)$$ -
ReLU6: tf.nn.relu6
$$f(x) = min(max(0, x), 6)$$ -
SReLU: Shift Rectified Linear Unit
$$f(x) = max(-1, x)$$ -
Leaky ReLU: Rectifier Nonlinearities Improve Neural Network Acoustic Models, ICML 2013
$$f(x) = max(\alpha x, x), \alpha =0.01 $$ -
PReLU: Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification, arXiv 2015
$$f(x) = max(ax, x), a\in [0,1), \alpha \text{ is learned}$$ -
RReLU: Empirical Evaluation of Rectified Activations in Convolution Network, arXiv 2015
$$f(x) = max(\alpha x, x), \alpha \text{~} U(l, u), l<u \ and \ l, u \in[0, 1)$$ -
CReLU: Understanding and Improving Convolutional Neural Networks via Concatenated Rectified Linear Units, arXiv 2016
$$f(x) = concat(\text{relu}(x), \text{relu}(-x))$$ -
离散的(Discrete)
-
NReLU: Rectified Linear Units Improve Restricted Boltzmann Machines, ICML 2010
$$f(x) = max(0, x+\mathcal{N}(0, \sigma(x)))$$ -
Noisy Activation Functions: Noisy Activation Functions, ICML 2016
简单绘制部分激活函数曲线:
References: