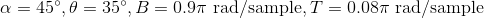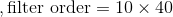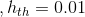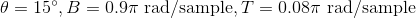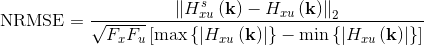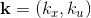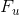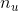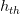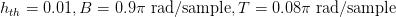This is a MATLAB implementation of the sparse FIR hyperfan filter for light field refocusing.
- Reference: Sanduni U. Premaratne, Chamira U. S. Edussooriya, Chamith Wijenayake, Len T. Bruton and Panajotis Agathoklis,"A 4-D Sparse FIR Hyperfan Filter for Volumetric Refocusing of Light Fields by Hard Thresholding," in Proceedings of International Conference on Digital Signal Processing, pp.1-5, 2018.
- e-print: A 4-D Sparse FIR Hyperfan Filter for Volumetric Refocusing of Light Fields by Hard Thresholding
- License: BSD 2-Clause
We kindly request you to cite the above paper in case you refer this work.
The input light field should be in MAT file format (.mat extension).
Parameters:
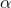 - Orientation of the fan filter in the
- Orientation of the fan filter in the 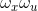 and
and 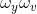 subspaces.
subspaces.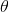 - Half fan angle.
- Half fan angle.- B - Length of the bow-tie shaped passband.
- T - Angular width of the bow-tie shaped passband.
Results for both sparse and nonsparse filters of the same parameters, are shown below for selected light fields of EPFL dataset for visual comparison. As a representative case, following values are chosen for the filter parameters 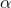 ,
, 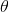 , B and T.
, B and T.
SSIM values of the volumetric refocused images obtained using the proposed sparse filter, with respect to those obtained using the nonsparse filter, are given below.
| Light field | Sparse filter | Nonsparse filter | SSIM |
|---|---|---|---|
| Flowers |  |
 |
0.9882 |
| Mirabelle Prune Tree |  |
 |
0.9714 |
| Sophie & Vincent 1 |  |
 |
0.9897 |
| Swans 1 |  |
 |
0.9916 |
Following is a visual comparison of output images obtained using the sparse filter with different 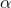 values, on selected light fields. Here,
values, on selected light fields. Here,
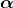 =60 =60 |
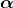 =105 =105 |
|
|---|---|---|
| Books |  |
 |
| Flowers |  |
 |
| Gravel Garden |  |
 |
| Sophie & Vincent 1 |  |
 |
| Swans 1 |  |
 |
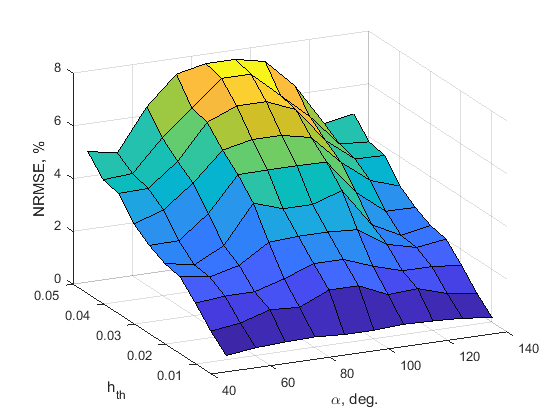
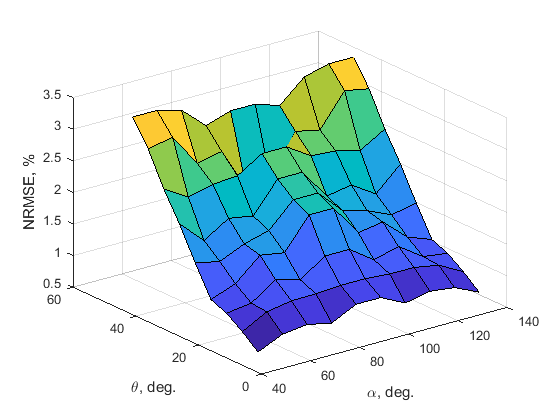
Normalized root mean square error (NRMSE) is used to quantify the deviation of the frequency response of the sparse filter compared to the nonsparse filter.
where,
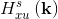 - Frequency response of the sparse filter
- Frequency response of the sparse filter
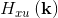 - Frequency response of the nonsparse filter
- Frequency response of the nonsparse filter
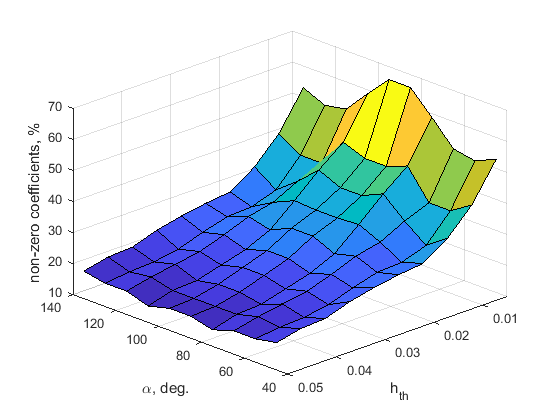
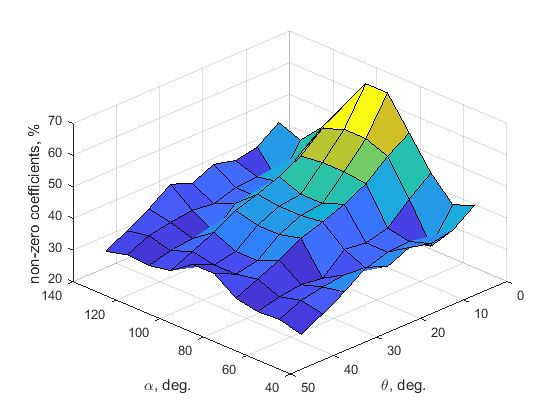
Furthermore, number of non-zero coefficients of the sparse filter with respect to that of nonsparse filter, can be used as a metric to evaluate the reduction of computational complexity.