I came up with my own Traveling Salesman Solution that creates a simple polygon (no intersecting sides) from a list of euclidean coordinate points. Then I spent a night demonstrating how bad it was.
Without going into too much background, it seemed intuitive (and ended up being mathematically correct) that an optimal path should not have intersecting paths. The Convex Hull algorithm is one I immediately found which took advantage of this.
My ELI5 of Convex Hull:
- Find the smallest polygon with only convex corners that encloses all the points
- Add the points inside the the polygon while minimizing cost (path length)
And to be fair, this is pretty cool and works great. But I couldn't figure out why my original idea wasn't as optimal:
What if I just average the points, get a center, and then go clockwise around it and find my path?
(Still doubting that this isn't a pre-existing solution which I somehow couldn't find while googling)
My ELI5 of the patented Tony Zhu Clock™ Algorithm:
- Attach a clock hand to the centroid found
- The order which points hit the hand as it spins clockwise is your path
- Solve P=NP and collect a cool 1 million dollars
Note: center point was eye-balled with sleep deprivation
The python program enclosed does the following:
- Generates N random points
- Solves using the Clock Algorithm
- Tries to beat it with brute force
- Graphs everything in a cute plot with animations
- Solves P=NP and collects a cool million dollars for me
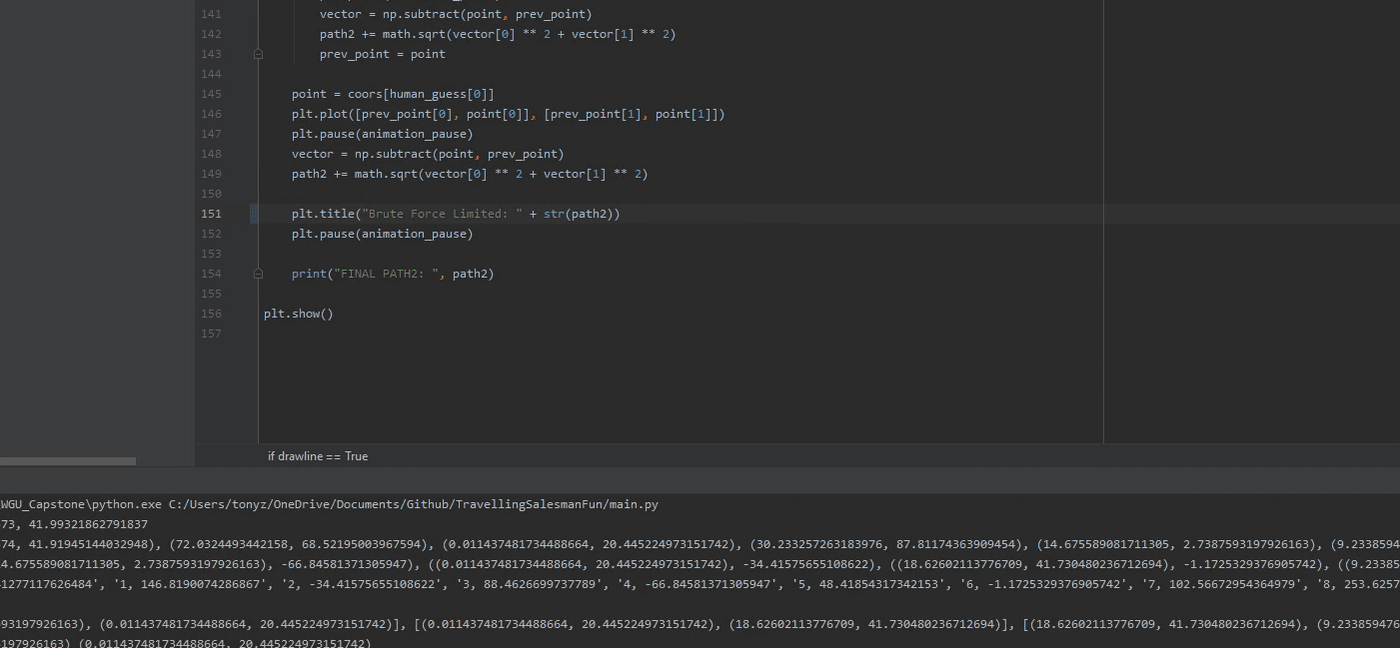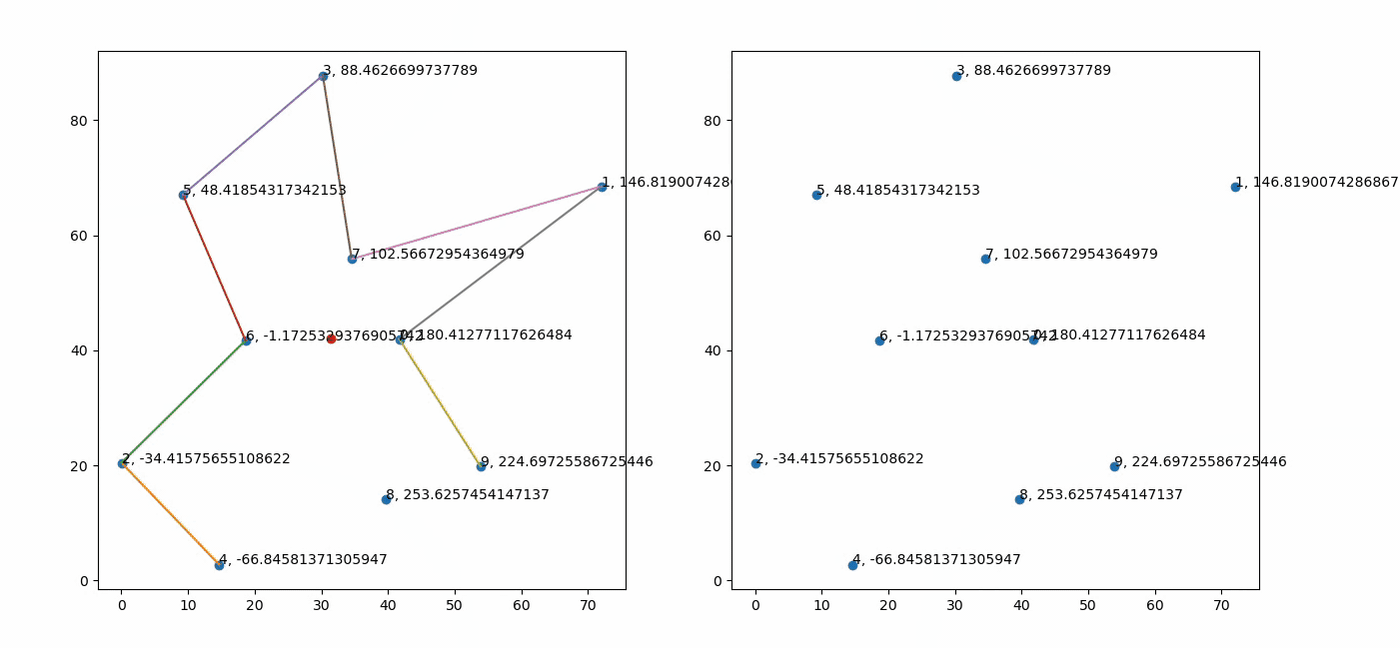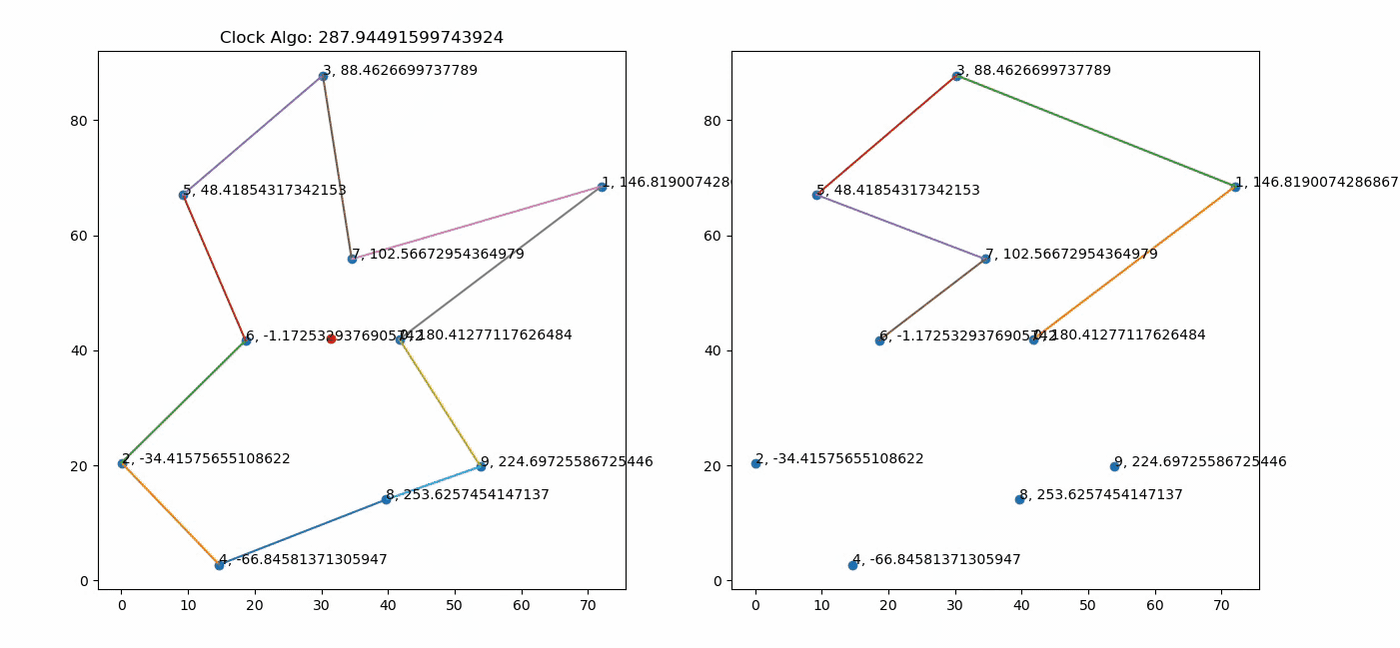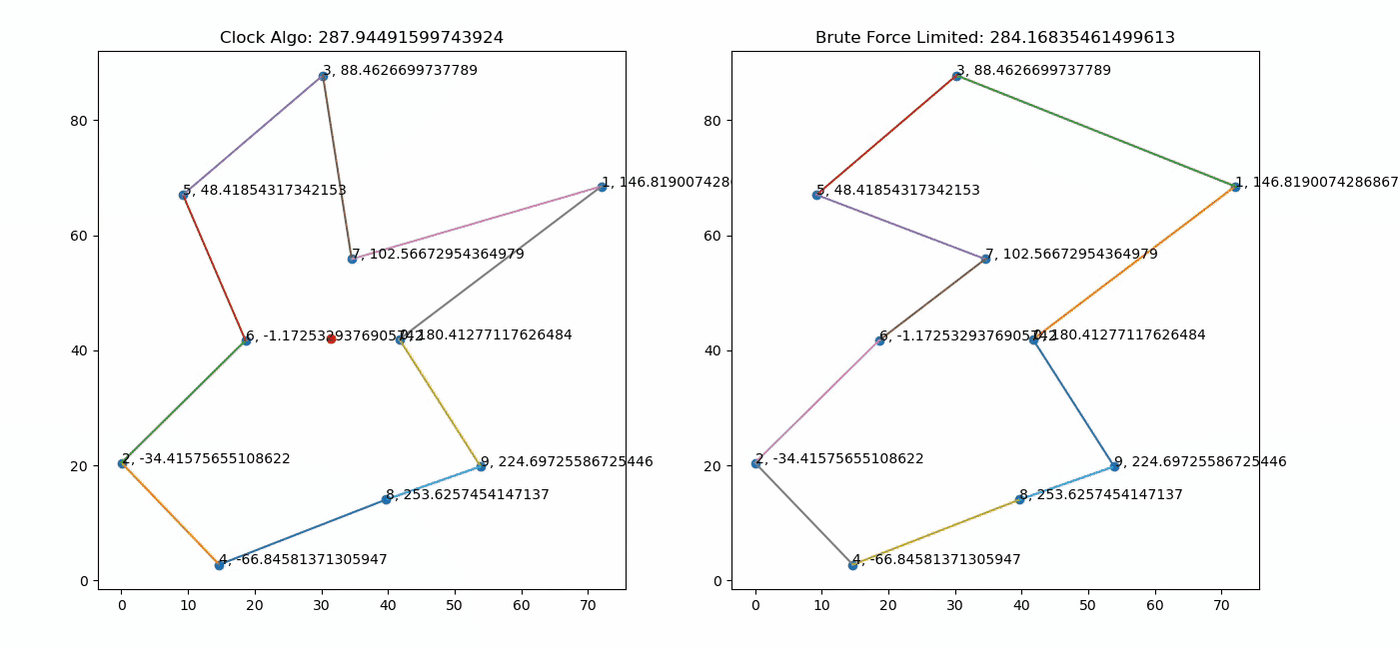
Final values in gif: Clock -> 287.9 | Brute Force Limited -> 284.2
I also want to take a moment to highlight (or lowlight) one of the more "wtf dumb/genius" things I've done in my life. In this program we run a recursive brute force method and then stop the recursion when we beat a pre-existing record. To "break;" out of the recursive function AND return a value (the new best path) I pulled the following move:
- If the new path length has reached the improvement threshold (i.e. we want anything that improves more than 1%)
- Raise an Exception and encode the return value in the error message
- Catch said Exception and use repr() to convert the message to a string
- Clean the string so it's just the payload
- Use eval() to make the python compiler evaluate the string as if it's code (an array)
- Bingo bango, recursion dead, new path acquired, P=NP solved
It mostly sucks.
Brute force is able to beat it if the number of points is below like 12. It's definitely nowhere near cranking out optimal paths or local minima. On the upside, for the time it takes to output a path that doesn't intersect itself, the algorithm is probably pretty speedy compared to its peers. Off the top of my head, the time complexity is O(n) for geometry stuff (angles, average center), plus O(nlogn) for sorting (angles in ascending/clockwise order).
If I ever come back to this, I definitely want to try slapping 2-opt onto that bad boy and seeing how good the solution can get at a rapid rate. There's a bunch of interesting patterns and math stuff I found on how to improve the Clock path and why it sucks to begin with, but that's a write-up for another time. In the same vein, it'd be cool to calculate most optimal (or best with current technology) paths and compare it to the Clock algorithm and Clock + 2opt. Another algorithm improvement idea I had was to generate curated lists of "centroids" and pick the best solution from those.
So to end the readme on a cheesy note: I still have hope for the Clock algorithm, because even broken it can be right twice a day.