solangii/MLP

Implement MLP using numpy

Course project of CSE463 Machine Learning, UNIST

Task

Our task is to train an MLP on$X_{tr}$, apply the trained MLP to the test set $X_{te}$, and visualize the corresponding test results. Our data are visualized in Fig. 1: The training set consists of 630 pairs of inputs and the corresponding ground-truth outputs: In Fig. 1(left), the location of each dot represents the corresponding training input $(x_1, x_2)$-coordinate values) while the class labels are highlighted by color. The accompanying Trn.txt file contains this training set: For each line, the first two columns represent an input $x = [x_1,x_2]^⊤$ and the third column provides the corresponding class label (0 or 1). The test set consists of 10,200 data instances and they are provided in Tst.txt file where two columns represent a test input per line.

Implement Detail

My MLP Architecture

Weight Initialization

• Using Xavier Normal Initialization for weight initialization

  Xavier Normal Initialization[Glorot & Bengio, AISTATS 2010]

$$ W \sim N(0,Var(W))\\ Var(W) = \sqrt{2 \over {n_{in}+n_{out}}} $$

​ ($n_{in}$ : # of previous layer's neurons, $n_{out}$ : # of next layer's neurons)

• Bias initialization as zero

Hyper-Parameter Setting

• Learning Rate : 1
• epochs : 50
• batch size : 1 (fully-SGD)
• using sigmoid for activation function

Performance

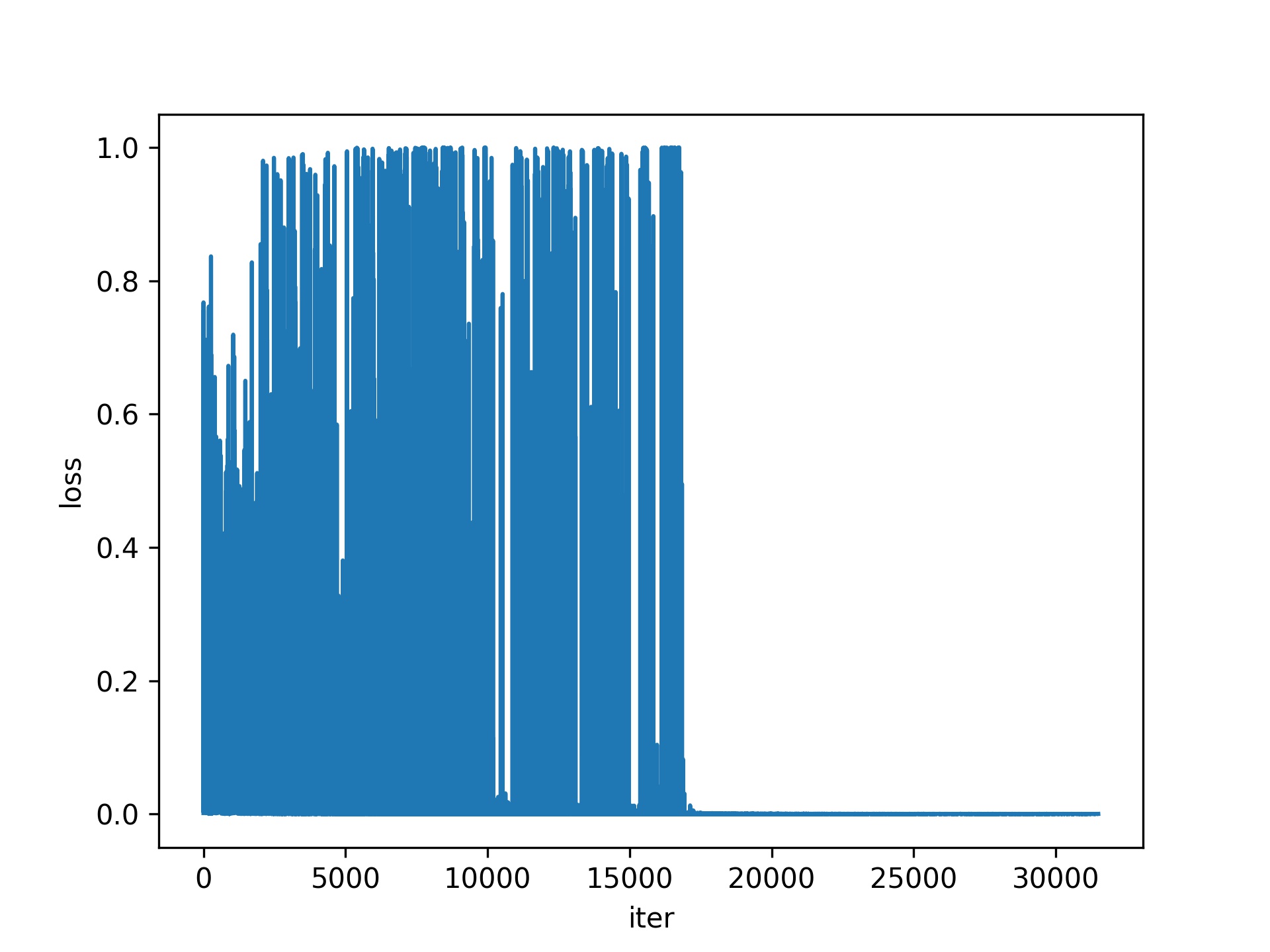
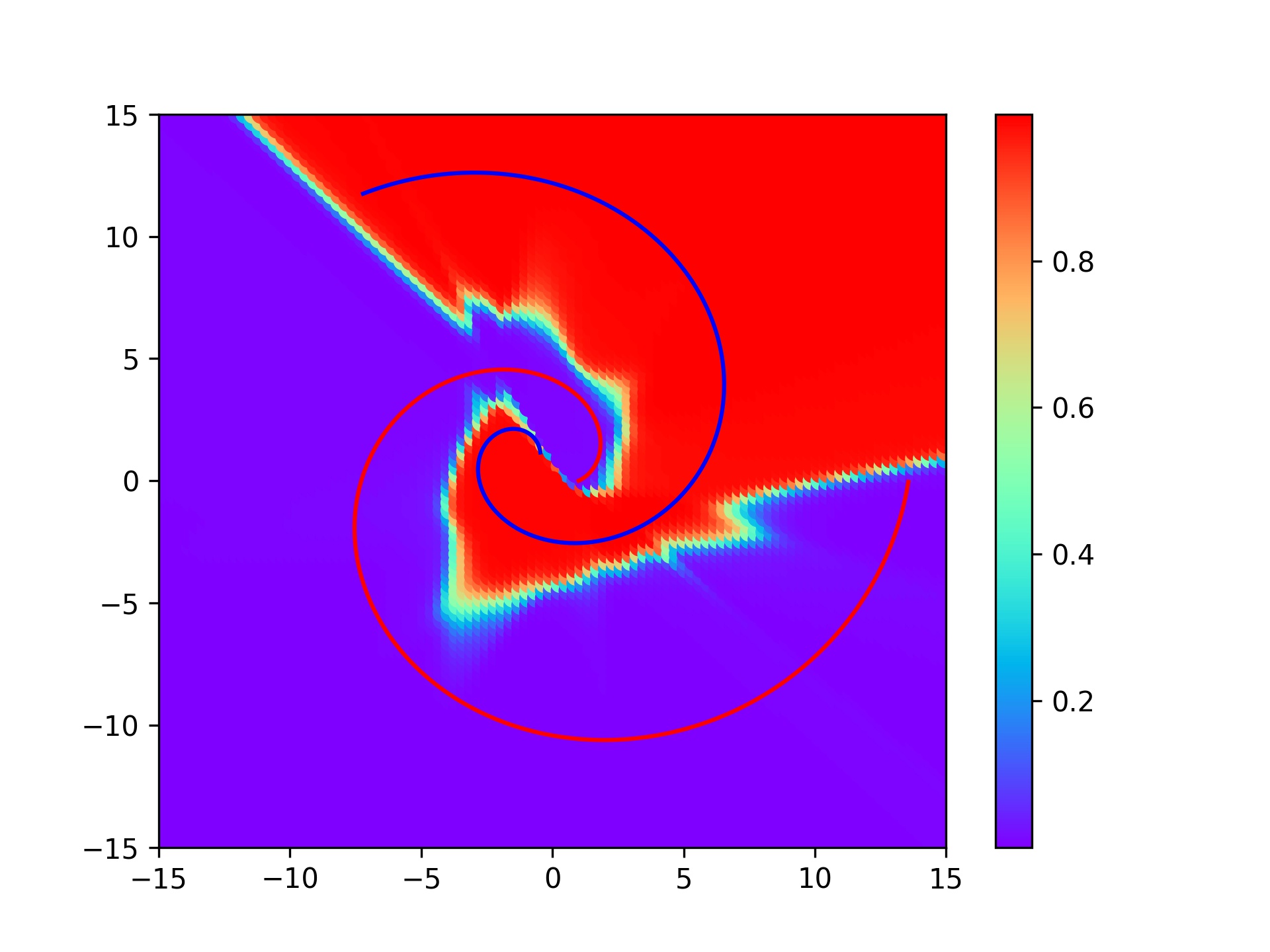
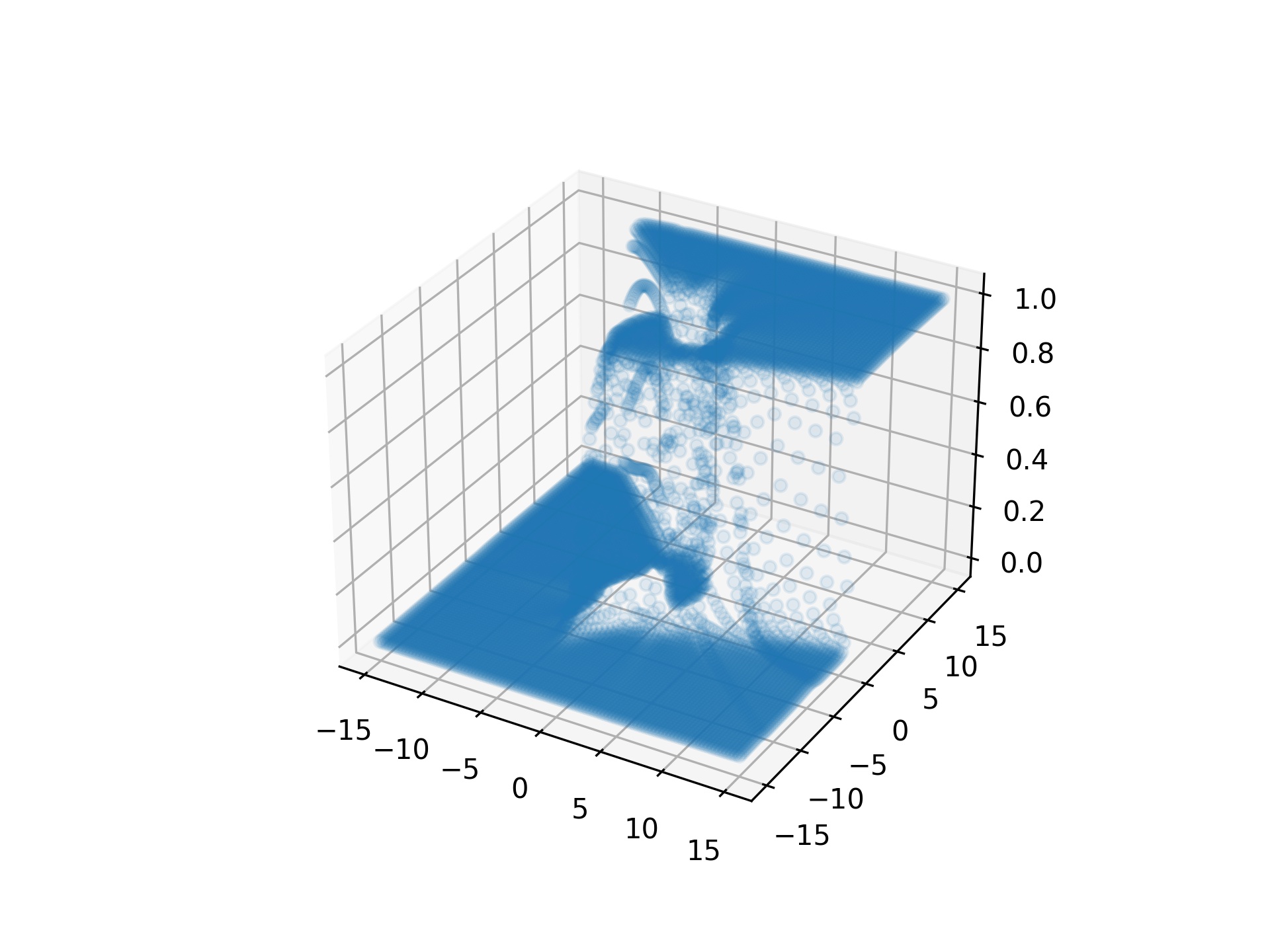
Loss	2D visualization	3D visualization

Additional Analysis

Except for the variable values regulated in the experiment, all values(hyper-params) are set to be the same.

Learning Rate

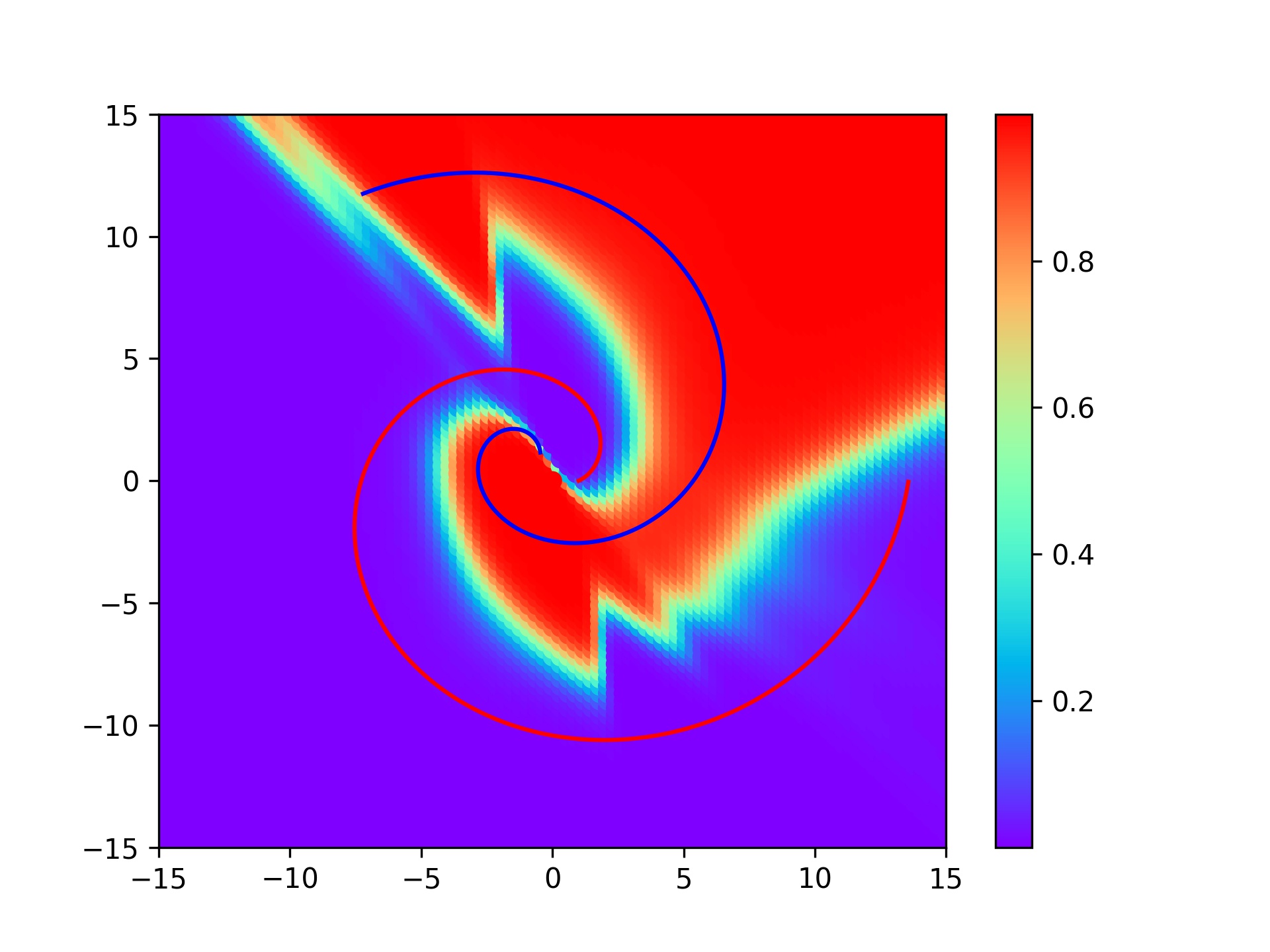
lr = 1 (base)	lr = 0.1	lr = 0.01

It appears to have found the appropriate learning rate value.

Epochs

Epochs = 50 (base)	Epochs = 30	Epochs = 10

Given the loss plot(loss graph), there has been no significant difference since it dropped sharply from about 10000-20000(iters), indicating that learning has been stable since epochs was about 15–30. Therefore, there is no significant difference between 30 and 50. I think It's okay to stop learning at a location where loss is moderately reduced(about epochs 15-30).

Number of Neurons (for Hidden Layer)

• h1: # of 1st hidden layer's neuron
• h2: # of 2nd hidden layer's neuron

h1 = 100, h2 = 50 (base)	h1 = 10, h2 = 5	h1 = 5, h2 = 2

It appears to have found the appropriate # of neuron value.