한눈에 살펴보는 딥러닝 관련 용어들
Neural Netowkrs는 Backpropagation 알고리즘을 통해 최상단의 레이어(아웃풋 레이어)로부터 최하단의 레이어(인풋 레이어)까지 오류를 역전파하는 방식으로 데이터에 적절한 파라미터 값을 같도록 학습을 진행한다. 이때 히든 레이어를 여러 층 쌓게 되면 아웃풋 레이어로부터 오류가 역전파 되면서 오류의 정보를 가지고 있는 경사값이 중간 히든레이어에서 사라지고 최하단의 인풋레이어까지 이 정보값이 전달되지 않는 문제가 있었다. 이런 문제를 Vanishing Gradient Problem(경사 사라짐 문제)이라고 한다. 이는 기존의 Neural Networks를 깊게(Deep) 쌓게 하지 못하는 근본적인 원인이었다. 이 문제를 해결하기 위해 Pre-training과 LSTM Networks 등의 방법이 제안되었고 현재는 이 문제를 상당 부분 해결했기 때문에 딥 러닝(Deep Learning)이 좋은 퍼포먼스를 보여주고 있다.
RNN에서 나타나는 시간에 따른 Vanishing gradient problem
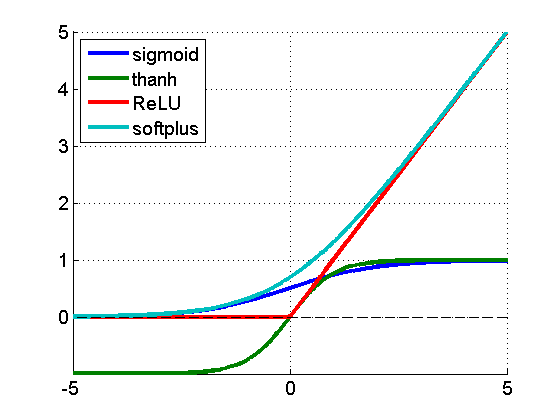
Rectified Linear Unit(ReLU)의 약자. Neural Networks의 Activation function 중 하나. 최근에 sigmoid activation function 대신 많이 사용된다.
f(x) = max(0,x) ~ ln(1+e^x)
로 정의된다. ReLU Activation function은 기존의 sigmoid activation function과 비교해서 다음의 두가지 장점을 가진다.
-
기존의 sigmoid activation function은 x의 값이 일정 수준 이상 커지거나 작아지면 gradient 값이 0이 되어 레이어를 깊게 쌓을 때 Vanishing Gradient Problem이 발생하였다. 이에 반해, ReLU activation function은 x가 0보다 크면 항상 1의 기울기를 가지므로 Vanishing Gradient Problem이 발생하지 않고, 더욱 바른 학습이 가능하다.
-
ReLU activation function의 경우 x가 0보다 작으면 0의 기울기 값을 가지므로 Hidden unit들이 sparse하게 특징을 학습하도록 유도할 수 있다.
여러 종류의 Activation Function들
Overfitting을 방지하기 위한 기법, Nueral Networks의 학습과정에서 node들을 일정 확률로 Drop(사용하지 않음)한다.
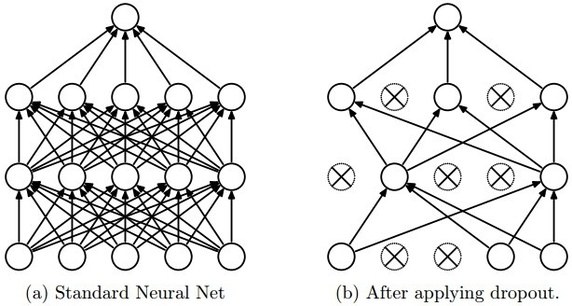
기본 Neural Networks와 Dropout을 적용한 Neural Networks
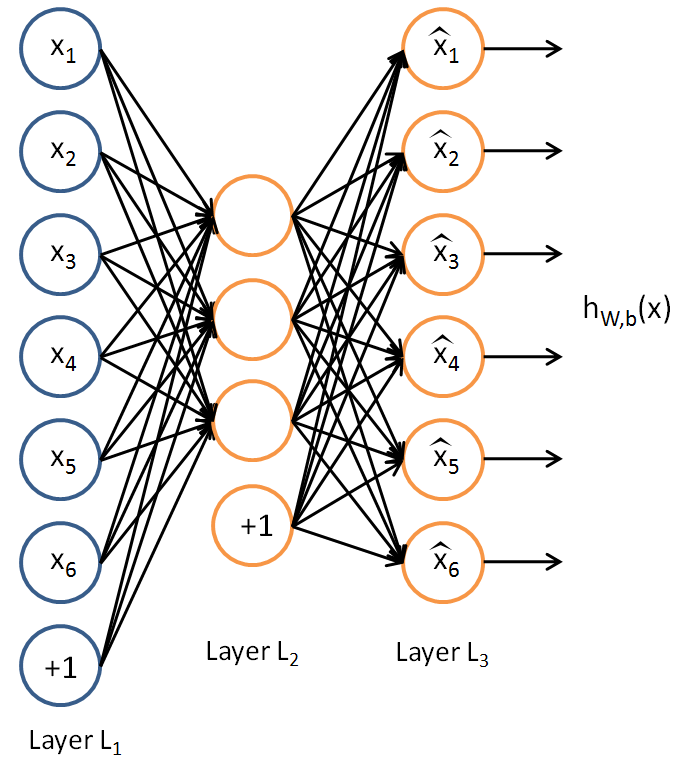
인풋과 아웃풋 노드의 개수가 같은 형태의 Neural Netowrks. Unsupervised Learning을 위해 사용된다. 인풋 노드와 아웃풋 노드의 수가 같으므로 항등 함수를 배우도록 training 된다. 이때 히든 레이어의 노드 개수가 아웃풋 레이어의 노드 개수보다 작으므로 히든 레이어는 인풋레이어에 관한 정보를 압축해서 저장해야만 한다. 따라서 히든 유닛들은 인풋 레이어에 대한 특징들(Features)을 저장하도록 학습된다. 따라서 이 히든 레이어의 아웃풋을 추출해서 유용한 특징(Feature)으로 사용할 수 있다.
Autoencoder의 Architecture
Autoencoder의 히든레이어의 아웃풋으로부터 추출된 특징들(Features)
Convolution Layer, Subsampling (Pooling) Layer, Fully Connetecd Layer로 구성된 Neural Networks. Supervised Learning을 위해 사용된다. 기존의 Neural Networks는 인풋 데이터 사이즈가 커지면 계산량이 기하급수적으로 증가하는 문제점이 있었다. 따라서, 이미지와 같이 인풋 데이터의 dimension이 큰 경우를 다루기 위해서 Convolution Neural Networks(CNNs)가 제안되었다. CNNs는 로우 인풋 데이터로부터 Convolution Layer를 통해 유의미한 피쳐들만을 추출하고, 이어서 Subsmapling (Pooling) Layer 를 통해 Convolution Layer로부터 추출된 결과값의 dimension을 축소시킨다. 이런 과정을 반복한 후 마지막 Fully Connetecd Layer에서 압축된 Feature를 통해 Classification과 같은 prediction을 수행한다. 현재 딥러닝이 적용가능한 대부분의 Task에서 활발히 사용되고 있는 가장 인기 있는 모델 구조이다.
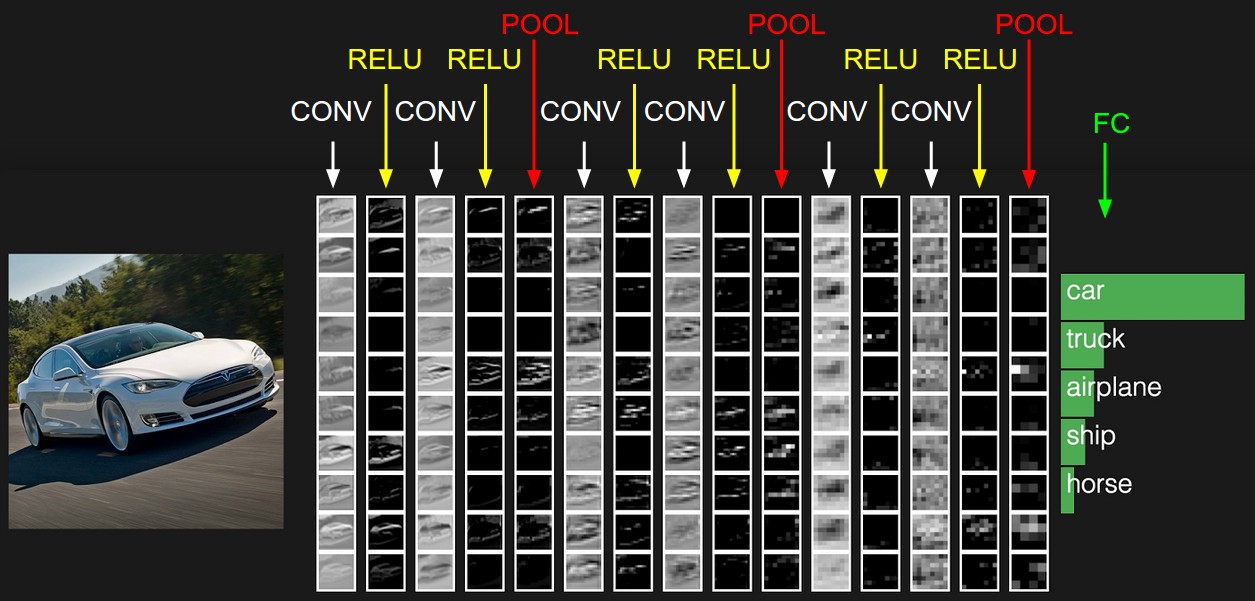
일반적인 Convolutional Neural Networks의 구조
기존의 Neural Networks의 Hidden Layer에 Self Connetecd Weight를 추가한 형태의 Neural Networks. Supervised Learning을 위해 사용된다. 기존의 Neural Networks의 경우 시간에 따른 데이터의 변화를 적절한 방법으로 저장하고 있을 수 있는 방법이 없었다. Recurrent Neural Networks는 이 문제를 해결하기 위해 히든 레이어에 Self Conneteced Weight를 추가함으로써 시간에 따른 데이터의 변화를 다룰 수 있게 되었다. 시계열 데이터 혹은 정적인 데이터도 시계열 형태로 표현하여 RNNs을 적용할 수 있다. 시계열 형태로 표현할 수 있는 Natural Language Processing (NLP)과 같은 도메인에서 활발히 사용되고 있는 추세이다.
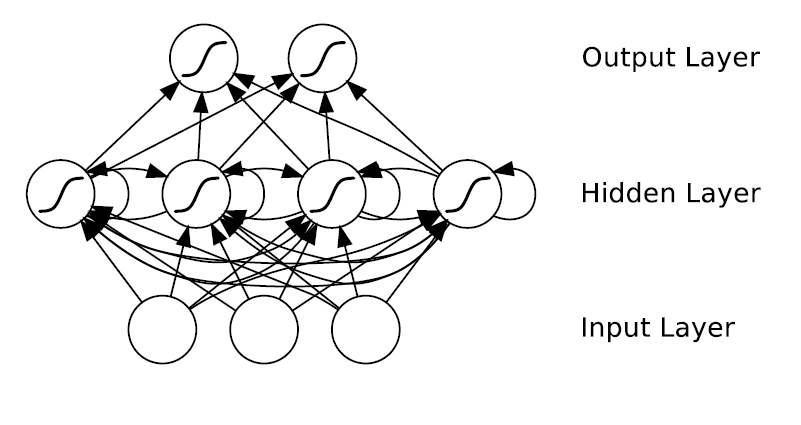
간단한 Recurrent Neural Networks의 구조
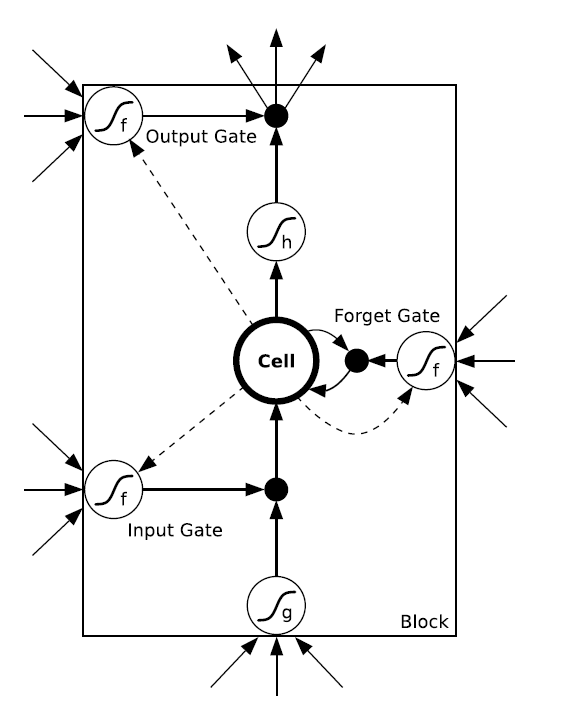
Recurrent Neural Networks (RNNs) 구조를 Vanishing Gradient Problem을 해결하기 위해 좀 더 복잡한 구조로 발전시킨 형태의 Neural Networks. LSTM Networks는 RNNs의 Hidden Layer를 Input Gate, Output Gate, Forget Gate라는 세가지 게이트로 구성된 Memory Block으로 대체한 구조이다.
Long Short-Term Memory(LSTM) Networks의 Memory Block