- Proof Techniques
- Set Theory
- Sequence & Tuple
- Graph Theory
- Formal Language Theory
- Grammar
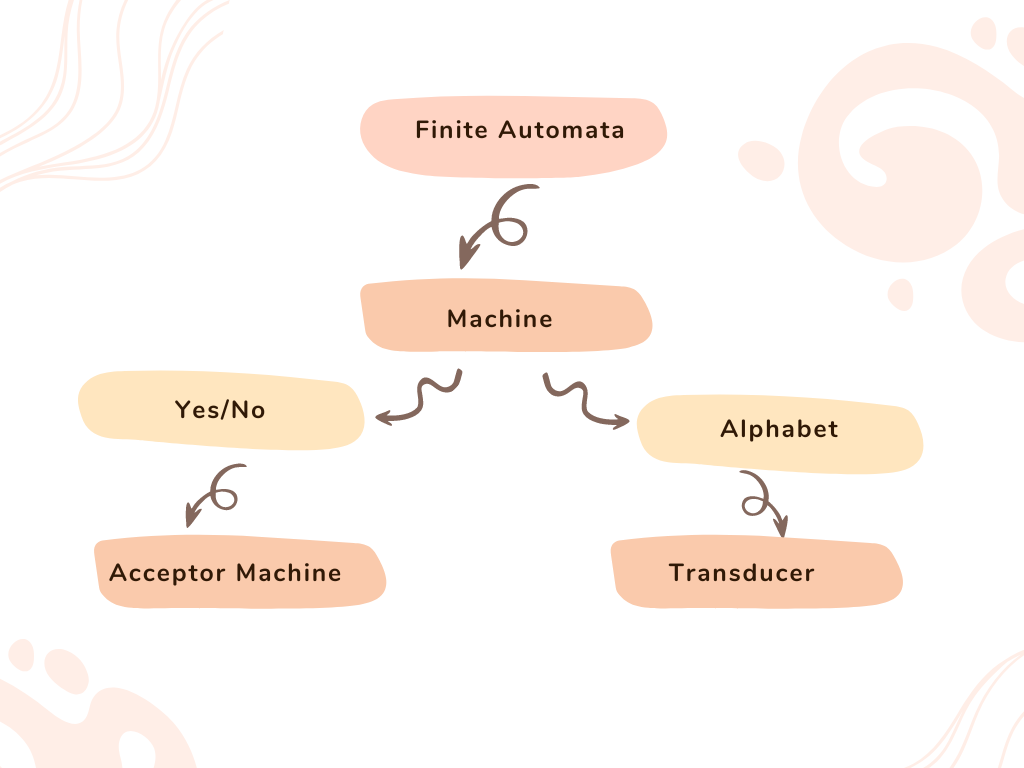
- Finite Automata
- Regular Expression
- Non-Deterministic Finite Automata
- NFA to DFA
- ∈ - NFA
- ∈ - NFA to NFA
- ∈ - NFA to DFA
- DFA State Minimization
- Pumping Lemma
In computer science, proof techniques are methods and approaches that are used to prove the correctness of algorithms and other logical statements.
Method of proof that involves directly showing that a statement is true, using logic and reasoning.
Theorem: If a and b are two even positive integers, then ab is always even.*
Proof:
Let a and b be two even positive integers.
By definition, an even number is a number that can be expressed in the form 2k .
Therefore, we can write:
a = 2x b = 2y
for some integers x and y.
Multiplying a and b, we get:
ab = (2x)(2y) = 4xy = 2(2xy)
This is an expression for an even number, because the coefficient of the term xy is even.
Therefore, ab is always even.*
QED
Theorem: If a is an odd integer and b is an even integer, then ab is always an even integer.*
Proof:
Let a be an odd integer, and let b be an even integer.
By definition, an odd integer is a number that can be expressed in the form 2x + 1 for some integer x. Therefore, we can write:
a = 2x + 1
for some integer x.
By definition, an even integer is a number that can be expressed in the form 2y for some integer y. Therefore, we can write:
b = 2y
for some integer y.
Multiplying a and b, we get:
ab = (2x + 1)(2y) = 4xy + 2y =2(2xy+y)
This is an expression for an even integer, because the coefficient of the term 2m is even.
Therefore, ab is always an even integer.*
QED
Proof by contradiction is a method of proof that involves assuming that the statement being proved is false, and then showing that this leads to a logical contradiction.
*Theorem: The square root of 2 is an irrational number.
Proof:
Suppose, for the sake of contradiction, that the square root of 2 is a rational number. This means that it can be expressed as the ratio of two integers p and q, where q is not equal to 0 and HCF (p, q) =1.*
We can write this as:
*√2 = p/q
Squaring both sides of this equation, we get:
2 = (p/q)² = p²/q²*
2q²=p²——— (i)
here, p² is even that mean p is even
then p = 2x
put in equation (i)
2q²= 4x
q² = 2x
q² is even then , q is even
Since p and q are even number so there HCF(p, q)!=1.
*Therefore, our assumption that √2 is a rational number must be false. This means that √2 is an irrational number.
QED*
Theorem: The square root of 3 is an irrational number.
Proof by induction is a method of proof that is used to establish that a given statement is true for all positive integers n. It involves showing that the statement is true for the base case n = 1, and then using the assumption that the statement is true for some arbitrary positive integer k to show that it is also true for k + 1.
*Theorem: For all positive integers n, 1 + 2 + 3 + ... + n = n(n+1)/2.
Proof:
Base case: We will show that the statement is true for*
n = 1 — 1 = 1(1+1)/2
1 = 1
n = 2 — 1+2 = 2( 2+1)2
3 = 3
then
n = k
1+2+3+4+….+k = k(k+1)/2
n = k+1
1+2+3+4+….+k+(k+1) = k(k+1)/2 + (k+1)
(k+1)(k+1+1)/2= (k+1)((k+1)+1)
*This is the expression for the sum 1 + 2 + 3 + ... + (k+1).
Therefore, we have shown that if the statement is true for some positive integer k, then it is also true for k + 1.
Since the statement is true for the base case n = 1, and we have shown that if it is true for some positive integer k, then it is also true for k + 1, we can conclude by induction that the statement is true for all positive integers n.
QED*
Theorem: For all positive integers n, 5 + 10 + 15 + ... + 5n = 5n(n+1)/2.
G = ( V, E)
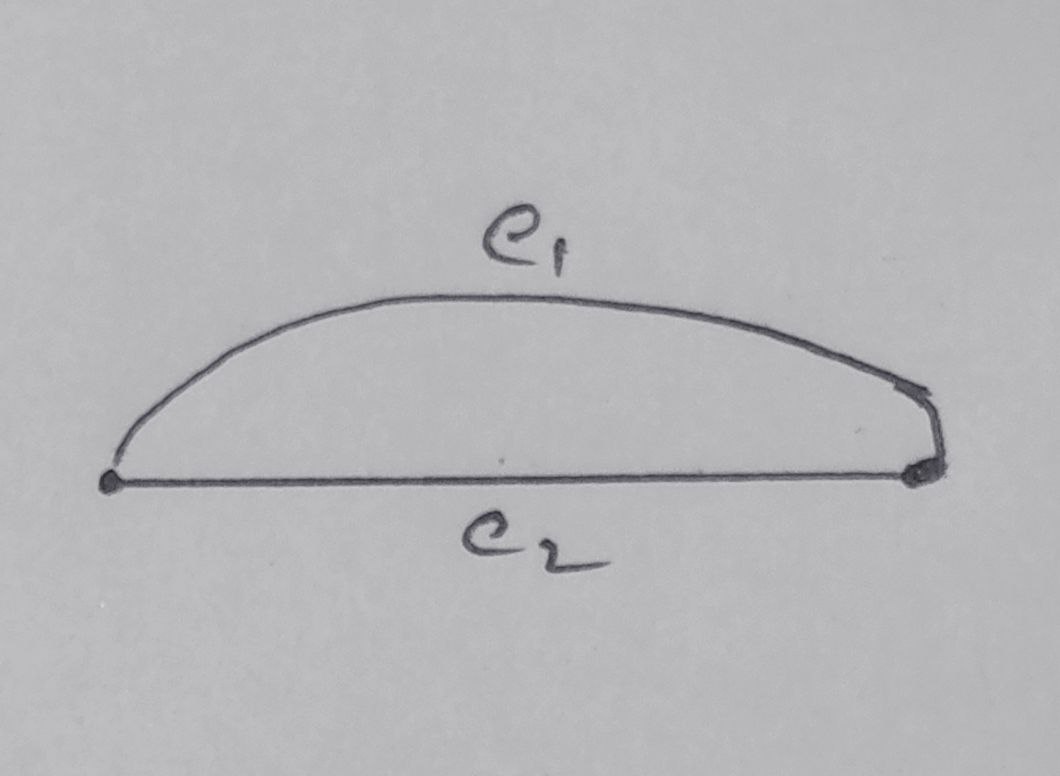
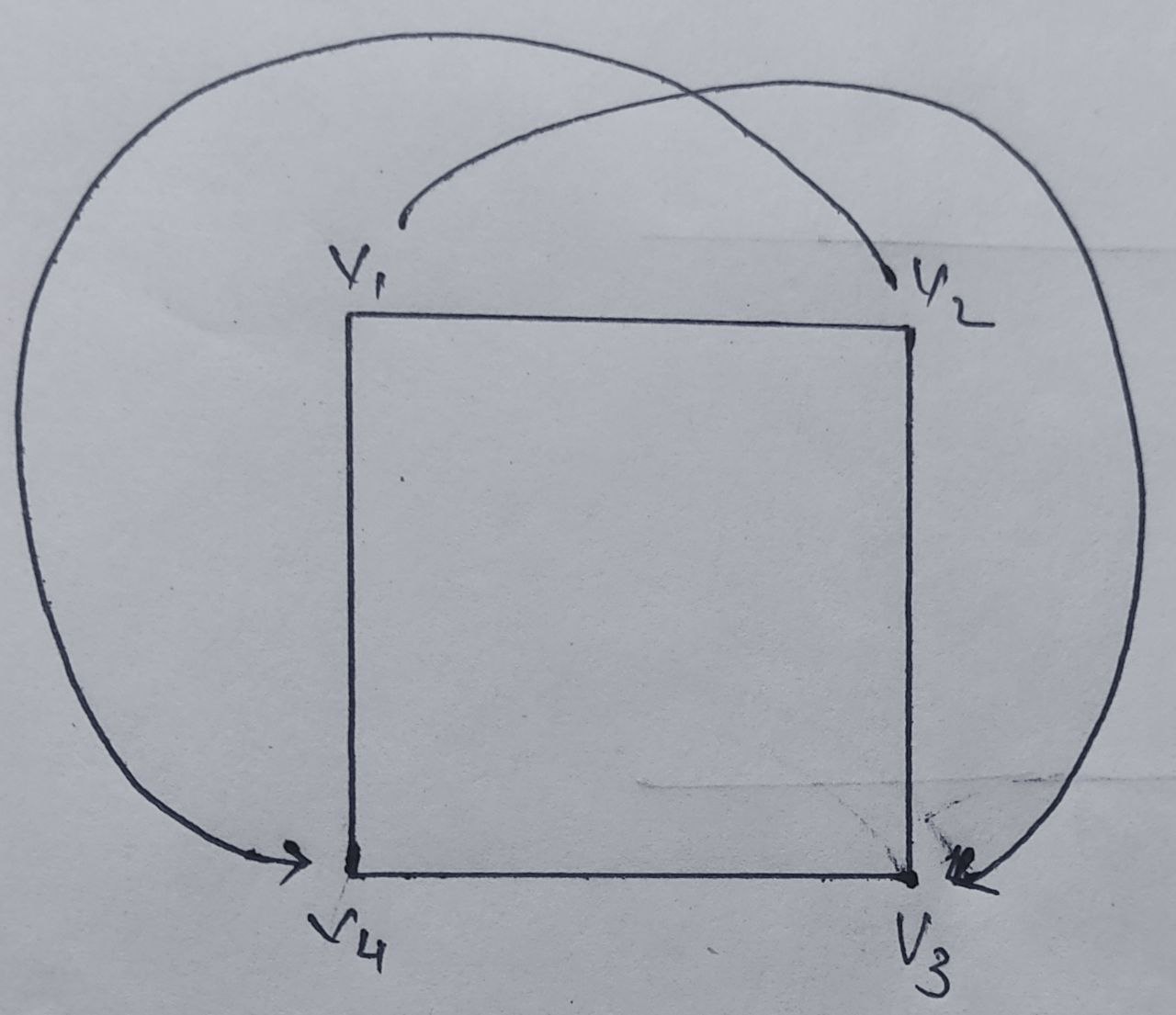
Loop : it is a path that begins and ends at the same edge.
Parallel edges : Parallel edges are two or more edges that connect the same two vertices.
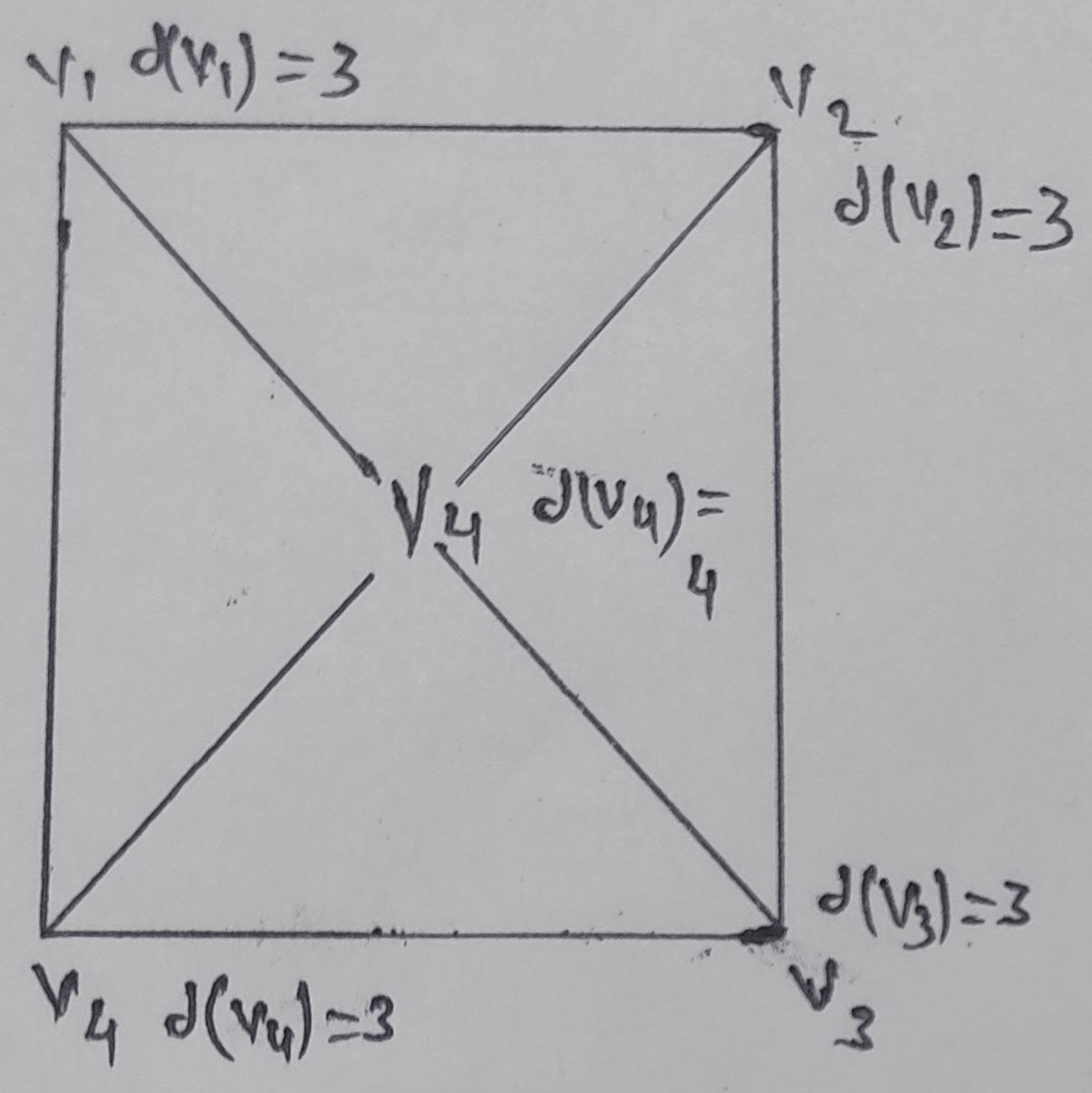
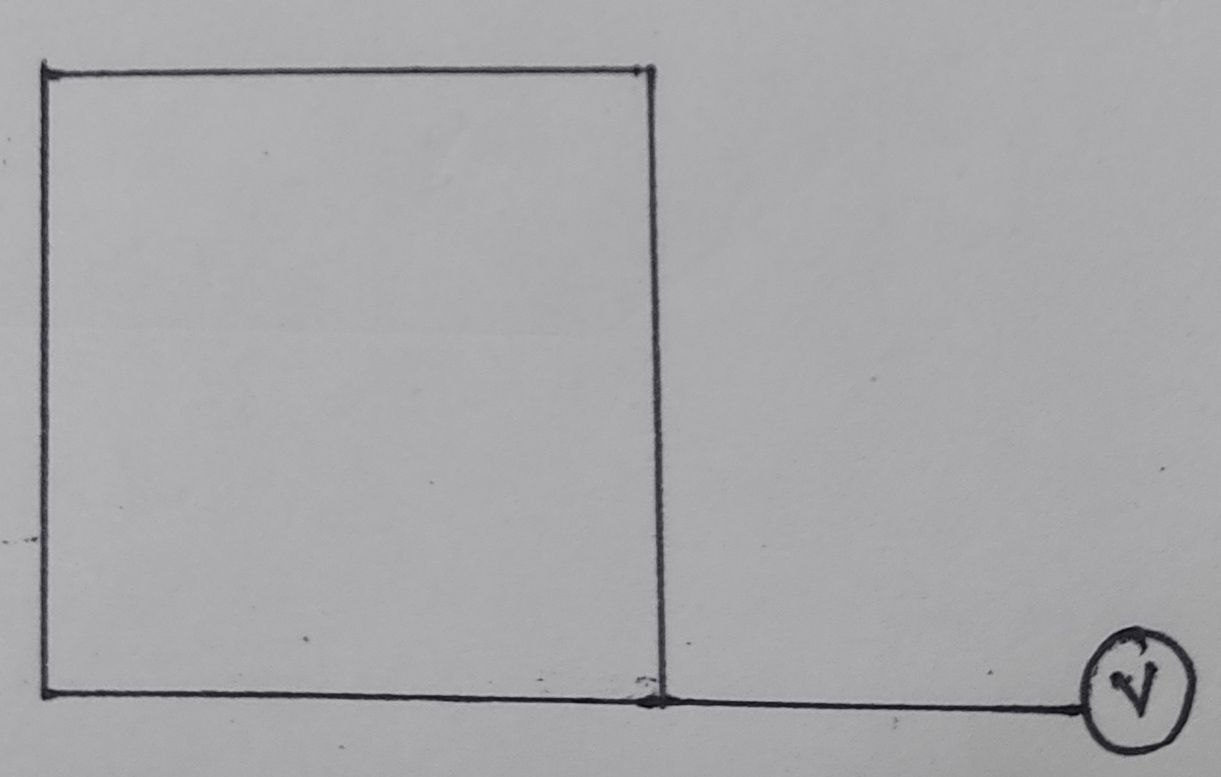
Degree of vertex [deg(v)] : Degree of a vertex is a measure of the number of edges incident to it, or connected to it.
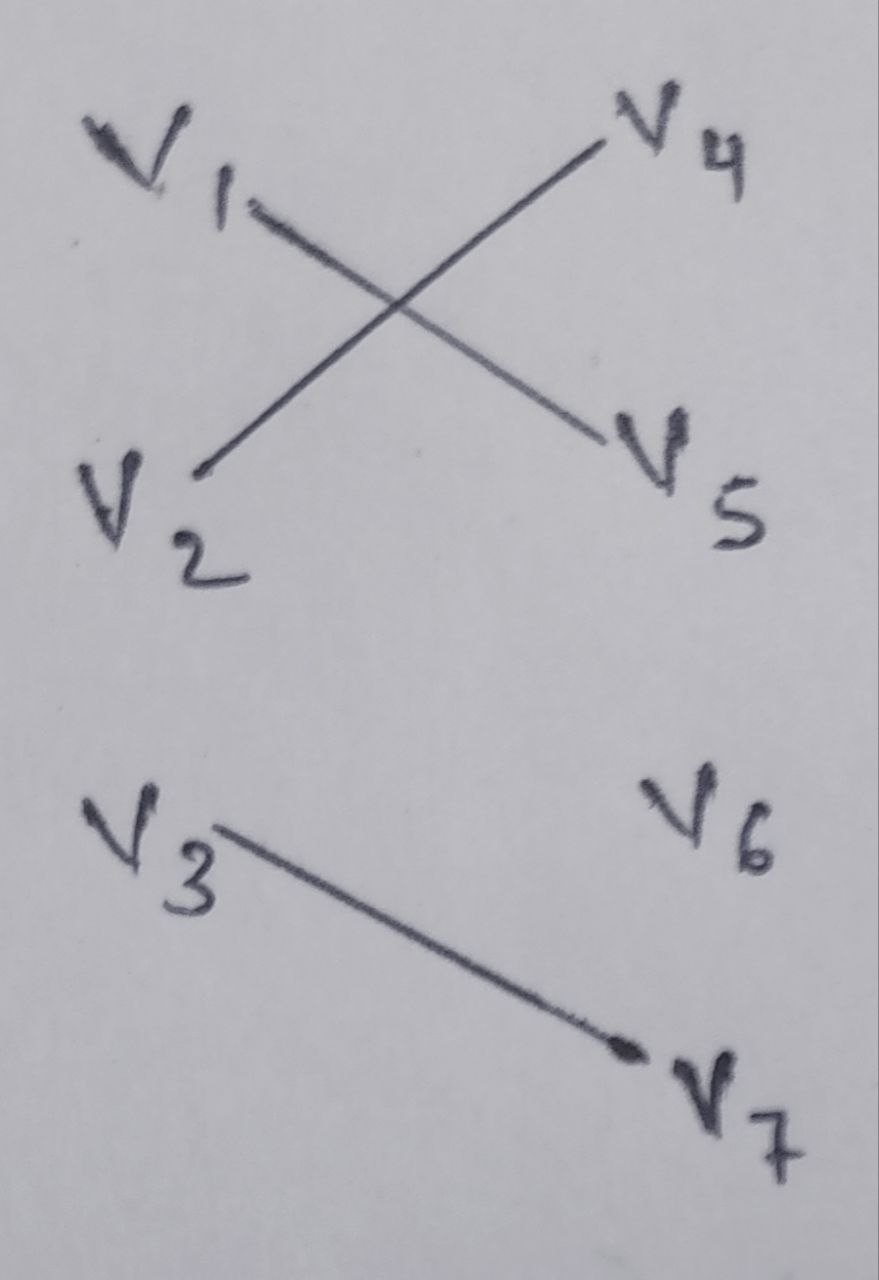
Indegree [deg-(v)] : Indegree of a vertex is the number of edges pointing towards it.
Indegree of vertex v1 is 2
deg-(v1) = 2
deg-(v2)= 2
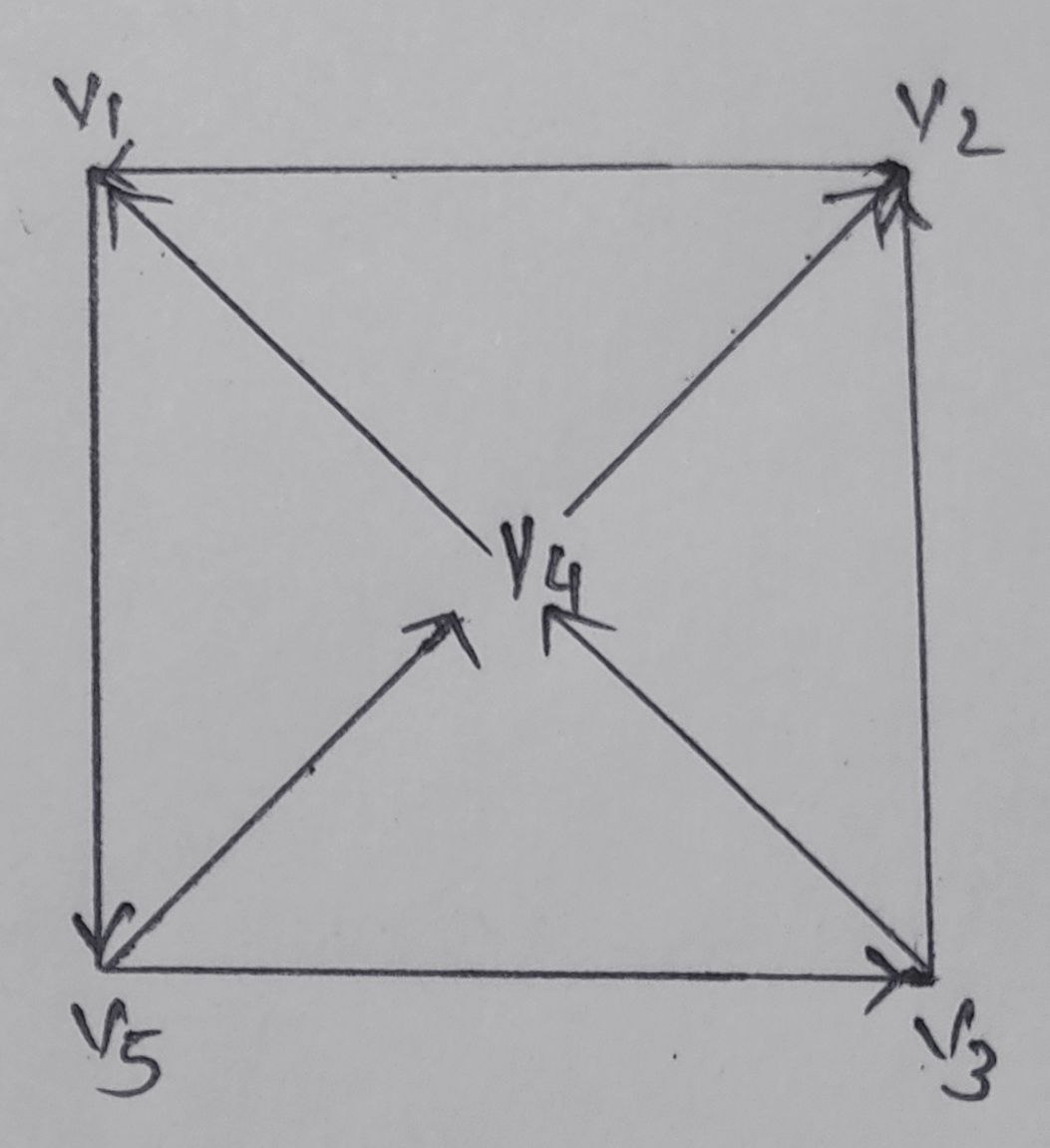
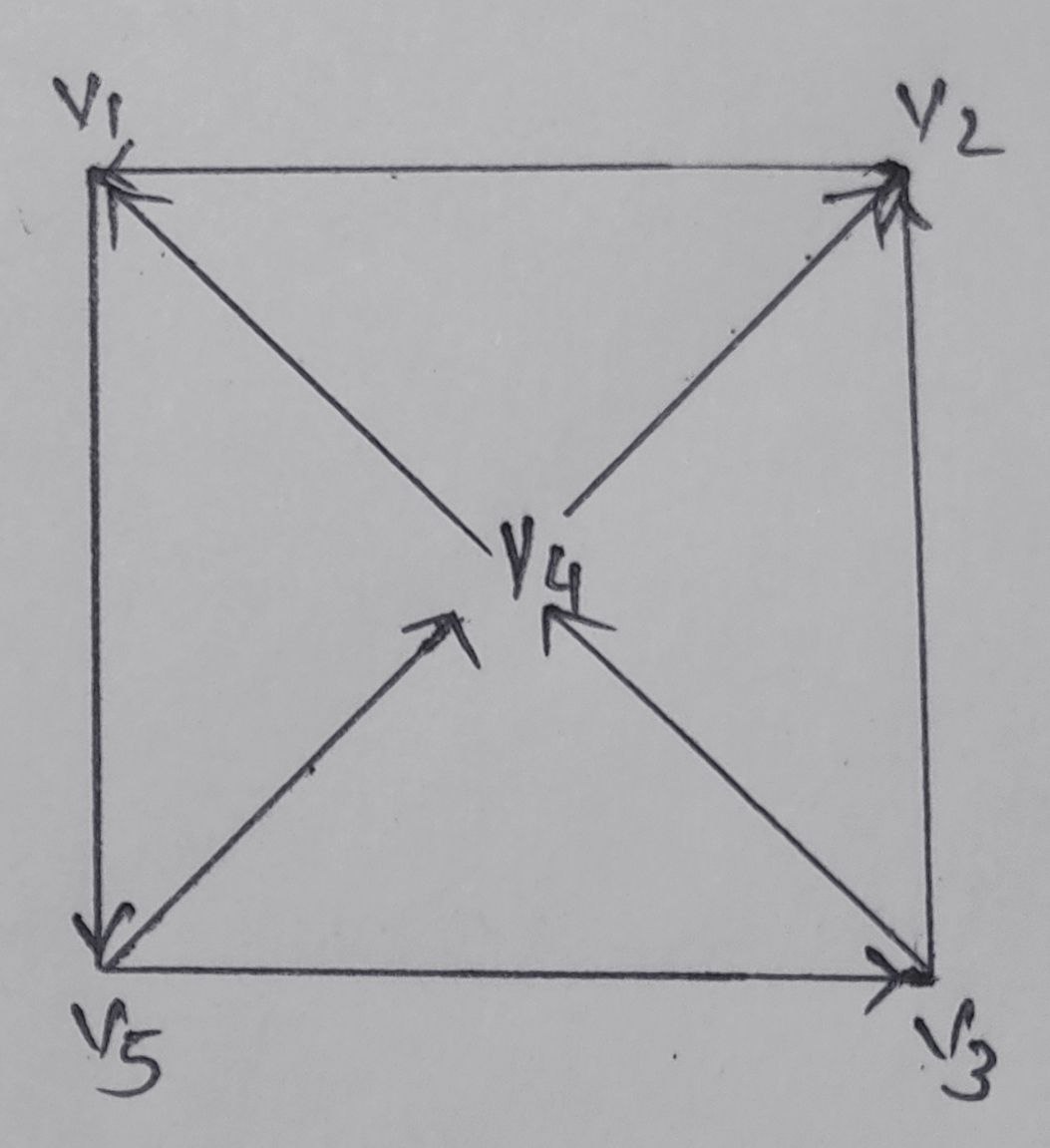
Outdegree [deg+(v)] : Outdegree of a vertex is the number of edges pointing away from it.
Outdegree of vertex v1 is 1
deg+(v1) = 1
deg+(v2)= 1
In Undirected graph :
In Directed graph :
Isolated Vertex : If the degree of a vertex is 0, the vertex is an isolated vertex and is not connected to any other vertices.
deg(v)= 0
Pendent Vertex :
deg(V) = 1
Simple Graph : No loop / No multiple edge.
Multiple Graph : Which have atleast one mutli or parallel edge.
Distance b/w two vertices : Minimum number of edges that must be traversed to go from one vertex to the other.
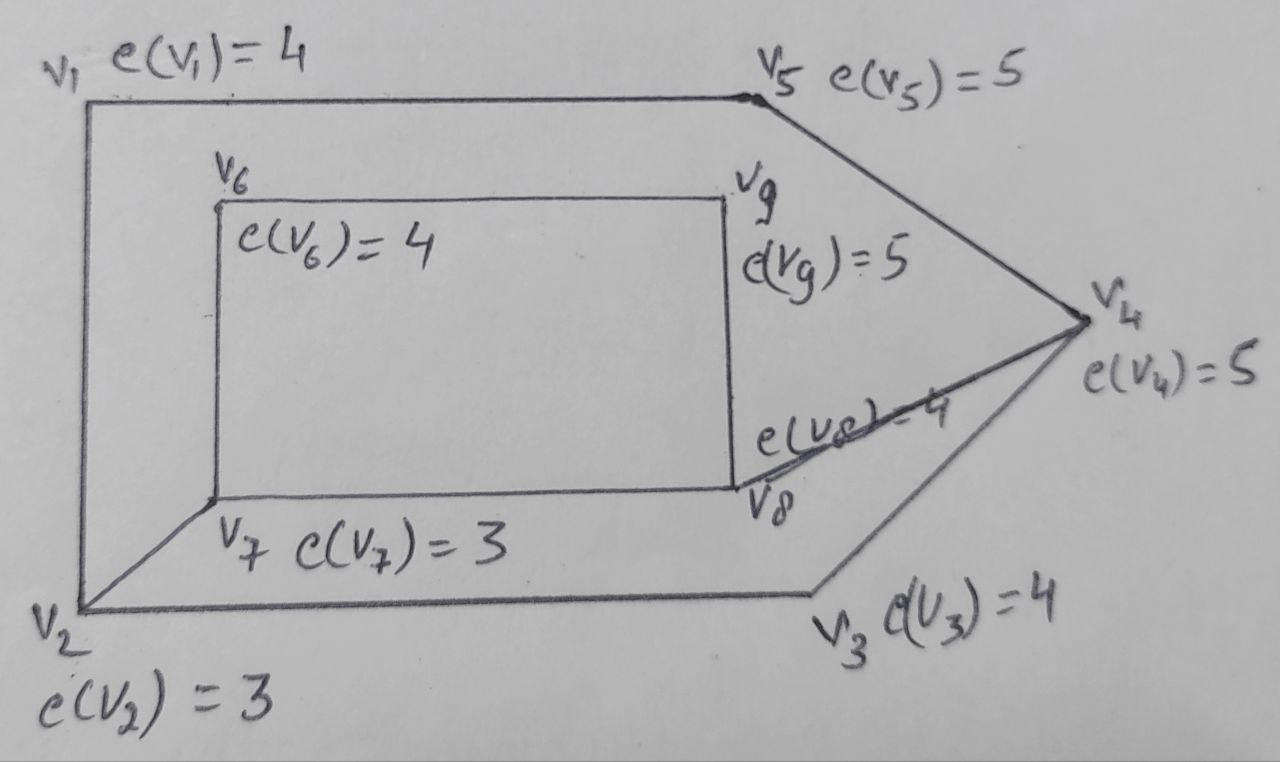
Eccentricity of vertex : The eccentricity of a vertex v, denoted as e(v), is defined as the maximum distance from v to any other vertex in the graph.
Radius of Graph : Radius of a graph is a measure of the centrality of the graph. It is defined as the minimum eccentricity of any vertex in the graph. r(G)
$r(G) = 1$
In this case, the minimum distance is 1, which occurs for the distances from v1 to v2, v5, and v6. Therefore, the radius of the graph is 1. r(G) = 3
Note : that the radius of a graph is the minimum eccentricity of any vertex in the graph, not just the minimum distance from a particular vertex (v1 in this case). To find the eccentricity of each vertex, you would need to find the maximum distance from that vertex to any other vertex in the graph.
*Diameter of Graph : The diameter of a graph is a measure of the centrality and the spread of the graph. It is defined as the maximum eccentricity of any vertex in the graph. D(G)
$D(G) = 5$
Center Point : The center of a graph is the set of vertices with the minimum eccentricity.
or
Center Point or
Center of The Graph :
e(Vi) = r(G)
Girth of a Graph : The girth of a graph is the length of the shortest cycle (a path that starts and ends at the same vertex) in the graph. The girth of a graph, denoted as g(G), is defined as the minimum length of any cycle in the graph.
*Circumference of Graph : The circumference of a graph is the length of the longest cycle (a path that starts and ends at the same vertex) in the graph. The circumference of a graph, denoted as C(G), is defined as the maximum length of any cycle in the graph.
-
Finite Graph
$e,v - Finite$
-
Infinite Graph
$e,v - Infinite$
-
Trivial Graph
Only one vertex
-
Simple Graph
No loop
No multiple edges
-
Multi Graph
Which have atleast one multi or parallel edges
-
Null Graph
A null graph is a graph in which there are no edges between its vertices. A null graph is also called empty graph.
-
Complete Graph
a complete graph is a graph in which every pair of distinct vertices is connected by an edge. A complete graph with n vertices is denoted as Kn.
-
Regular Graph
Regular graph is a graph in which all the vertices have the same degree (i.e., the same number of edges).
K - regular graph
deg(vi) = K
This graph is 2-regular graph
-
Bipartite Graph
Bipartite graph is a graph whose vertices can be divided into two disjoint sets such that every edge in the graph connects a vertex in one set to a vertex in the other set.
-
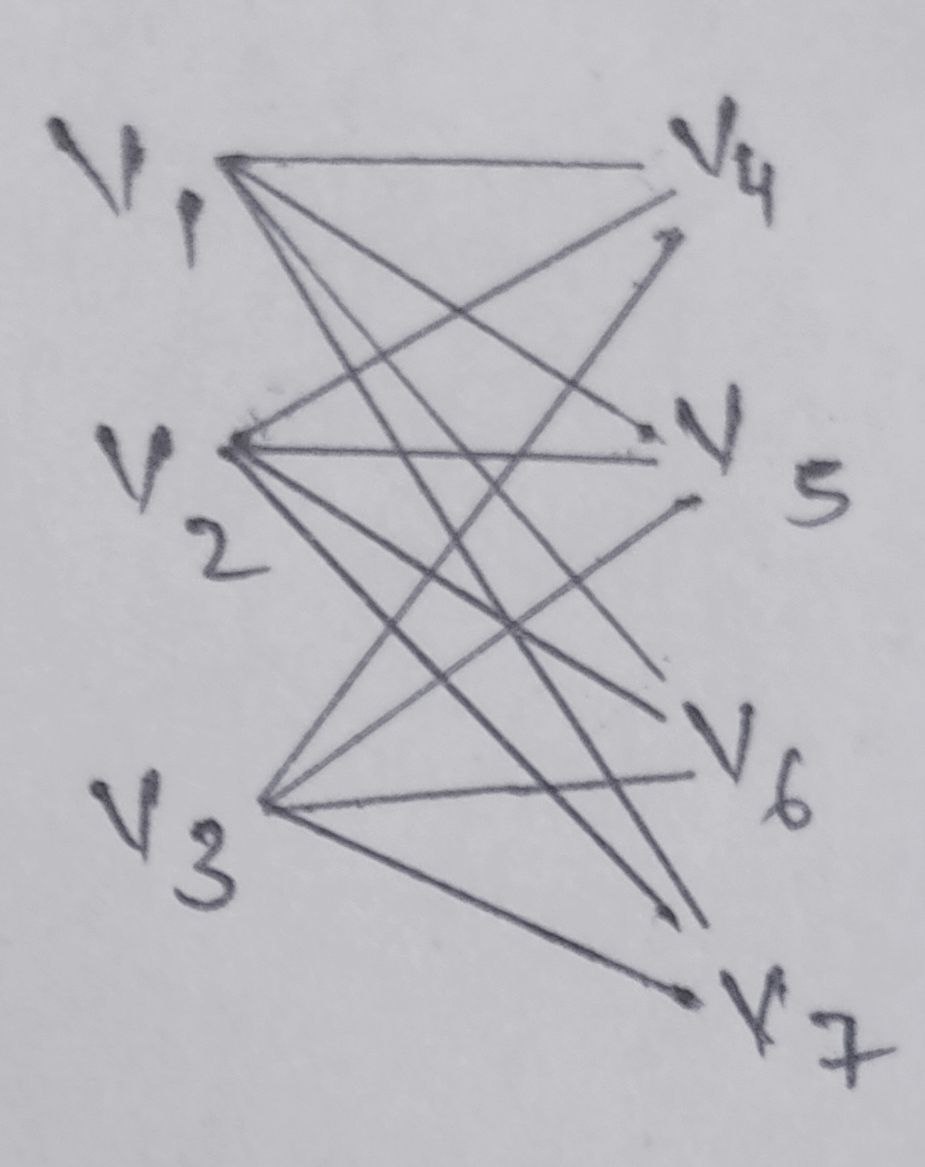
Complete Bipartite Graph
A complete bipartite graph is a bipartite graph in which every vertex in one set is connected to every vertex in the other set.
-
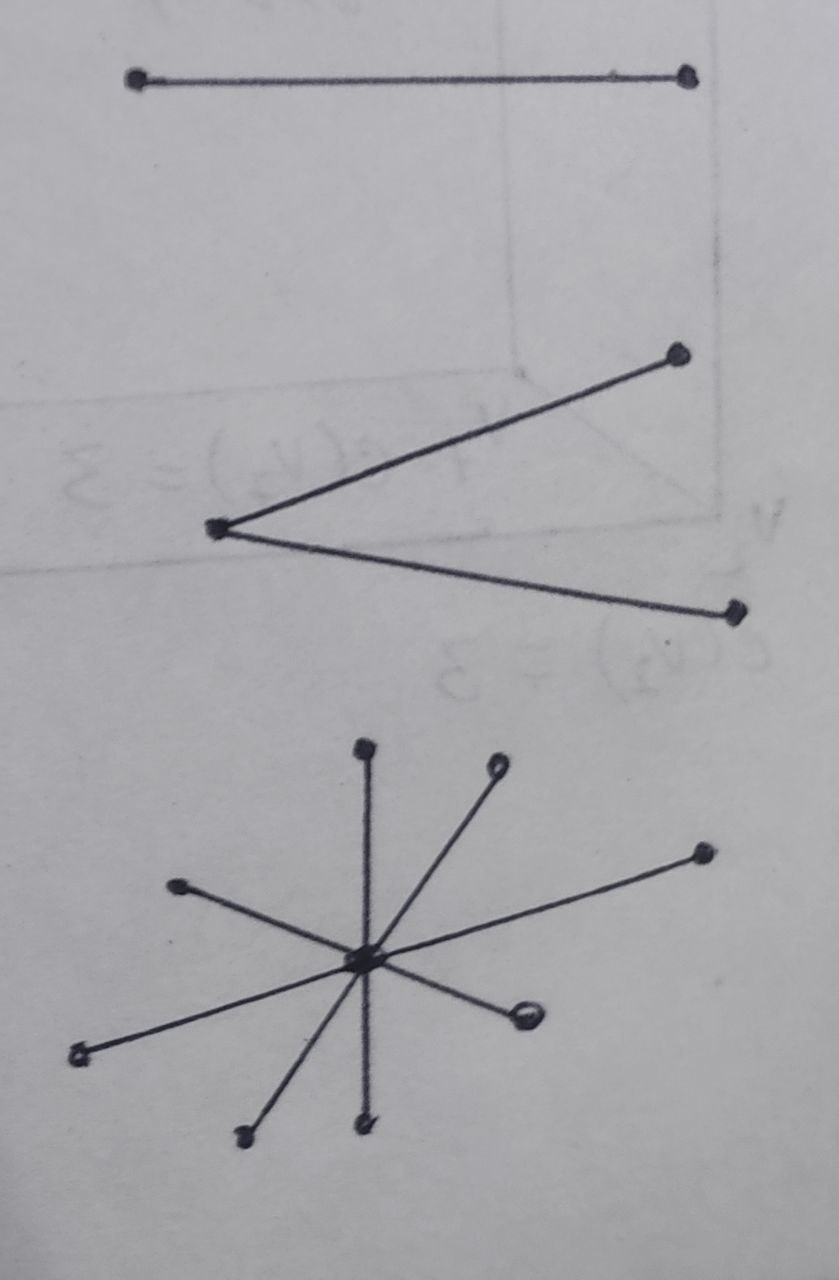
Star Graph
Case I : Distance between two vertexes(Vi) is same
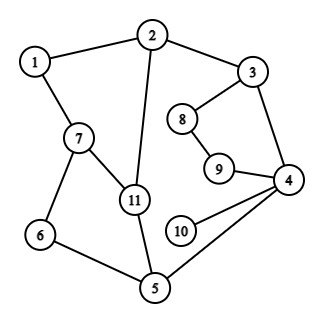
Q : We have 11 villages and have to place 3 shops in between them. Find the locations of the villages where you can place the shops.
Eccentricity e(Vi)
e(1) = 4 D(1 to 9)
e(2) = 3 D(2 to 9)
e(3) = 3 D(3 to 7)
e(4) = 3
e(5) = 3
e(6) = 4
e(7) = 4
e(8) = 4
e(9) = 4
e(10) = 4
e(11) = 3
For 3 shops we can choose any 3 from
{2,3,4,5,11}
Case II : Distance between two vertexes(Vi) is not same
Q : We have 11 villages and have to place 3 shops in between them. Find the locations of the villages where you can place the shops.
d(1, 2) = 2
d(1, 3) = 5
d(1, 4) = 7
d(1, 5) = 3
d(1, 6) = 2
d(1, 7) = 1
d(1, 8) = 7
d(1, 9) = 8
d(1,10)=10
d(1, 11) = 2
d(2, 1) = 2
d(2, 3) = 3
d(2, 4) = 5
d(2, 5) = 4
d(2, 6) = 4
d(2, 7) = 3
d(2, 8) = 5
d(2, 9) = 6
d(2,10)=8
d(2, 11) = 3
d(3, 1) = 5
d(3, 2) = 3
d(3, 4) = 2
d(3,5)=7
d(3,6)=7
d(3, 7) = 6
d(3, 8) = 2
d(3, 9) = 3
d(3, 10) = 5
d(3, 11) = 6
For 3 shops we can choose
{2,3,5}
Q : Put a village (v=12) in case I and case II
Symbol : A symbol is a basic unit of a language.
Alphabet : Finite set of symbols. Ex : Σ= {0,1}
String : Sequences of symbols drown from alphabet (finite length).
-
Language : Collection of string drown from alphabet.
Finite : A finite language is a language that contains a finite number of strings.
For example, the set of all strings that are made up of the letters 'a' and 'b' and have a length of less than 5 is a finite language.
Infinite : A infinite language is a language that contains an infinite number of strings.
For example, the set of all strings that are made up of the letters 'a' and 'b' is an infinite language. The set of all strings that starts with 'a' and ends with 'b' is also an infinite language.
Σ = {0,1}
L = { aⁿ bⁿ | n>0 and n≤2 }
L = { ab,a²b² }
a² = a.a = aa
a* = Repetition of a, 0 or more time.
ex : { a⁰ , a¹ , a² , a³ , a⁴ , ……….. }
a⁰ = **λ (Empty String)**a⁺ = Repetition of a, 1 or more time.
ex : { a¹ , a² , a³ , a⁴ , ……….. }
-
Prefix :
Prefix is any string that will obtain after removing 0 and more character from end of string.
S = abcabca
Prefix :
abcabca - 0 char remove
λ - 7 char remove
abcabc - 1 char remove
abcab - 2 char remove
abca - 3 char remove
abc - 4 char remove
-
Suffix :
Suffix is the string that will be obtain after removing 0 or more character from front of the string
S = abcabca
Suffix :
abcabca - 0 char remove
λ - 7 char remove
bcabca - 1 char remove
cabca - 2 char remove
abca - 3 char remove
bca - 4 char remove
Proper Prefix or Suffix : All the prefix and suffix excluding { abcabca, λ }
Substring : Removing 0 or more character form beginning or from end.
-
Example :
w = 1010001
wᴿ = 1000101
Σ = {0, 1}
Σ* = { λ, 0 , 1, 00, 01, 10, 11, ……}
Σ⁺ = Σ* - λ
L = { 0ⁿ 1ⁿ | n≥0 }
L = { λ, 01, 0011, 000111, 00001111, ……..}
L’ = Σ* - L
Lᴿ = { 1ⁿ 0ⁿ | n≥0 }
L* = { λ, 0ⁿ1ⁿ, 0ⁿ1ⁿ0ⁿ1ⁿ, 0ⁿ1ⁿ0ⁿ1ⁿ0ⁿ1ⁿ, ……..}
Σ = { a, b }
L₁ = { aⁿ bⁿ cⁿ | n≥1 }
L₂ = { aᵐ bᵐ | m>0 }
L₁ U L₂ = { aⁿ bⁿ cⁿ U aᵐ bᵐ | n≥0 & m>0 }
L₁ U L₂ = { λ, abc, aabbcc, .…., ab, aabb, aaabbb, .…..}
L₁ ∩ L₂ = λ
L₁ . L₂ = { aⁿ bⁿ cⁿ aᵐ bᵐ | n≥1 & m≥0 }
-
Question :
Σ = {a, b}
Q - 1 : Define a language which container exactly 2 a’s.
L = { bⁿ a bⁿ a bⁿ }
Q - 2 : Prefix will be aba always.
L = { aba (a + b)ⁿ | n≥0 }
Q - 3 : Start with ‘a’ an with ‘b’.
L = { a (a + b)ⁿ b | n≥0 }
- T is a finite set of terminals, which are the basic symbols of the language.
- V is a finite set of non-terminals, which represent the variables or syntactic categories of the language.
- S is the start symbol, which is a non-terminal that represents the beginning of the derivation process.
- P is a finite set of production rules, which specify how strings in the language can be constructed by replacing non-terminals with strings of terminals and non-terminals.
Capital Symbols = V (non-terminals)
Σ (Small Symbols) = T (terminals)
Start Symbol = S
A → aAb / λ
V = { A }
T = { a, b }
S = { A }
-
Types of Grammars :
There are different types of grammars, each with their own set of rules and capabilities:
- Regular Grammar
- Context-Free Grammar
- Context-Sensitive Grammar
- Unrestricted Grammar
-
Example :
Σ = { a }
L = { a }
S → a
S = S
T = { a }
V = { S }
L = { aa }
S → aa
S = S
T = { a }
V = { S }
or
S → aB
B → a
S= { S }
T = { a }
V = { S, B }
1 :
L = { aⁿ | n>0 }
L = { a, aa, aaa, aaaa, .... }
S → aS / a
T = { a }
V = { S }
S = { S }
4 :
L = { aⁿ bᵐ | n,m>0 }
S → AB
A → aA / a
B → bB / b
T= { a, b }
V = { S, A, B}
S = { S }
2 :
L = { aⁿ | n≥0 }
L = { λ, a, aa, aaa, aaaa,...}
S → aS / Φ
T = { a}
V = { S }
S = { S }
5 :
L = { aⁿ bᵐ | n≥2, m≥3 }
S → AB
A → aA / aa
B → bB / bbb
T = { a, b }
V = { S, A, B}
S= { S }
3 :
L = { aⁿ | n≥k }
let k = 3
S → aS / aaa
T = { a }
V = { S }
S = { S }
6 :
L = { aⁿ bⁿ | n>0 }
S → aSb / ab
T = { a, b }
V = { S }
S = { S }
7 : L = { aⁿ bⁿ | n≥0 }
S → aSb / Φ
-
Question :
Q : Write a language that contains all the strings over the alphabet {a,b} such that the strings have exactly 2 b’s.
Σ = { a, b }
L = { aⁿ b aⁿ b aⁿ | n≥0 }
S → AbAbA
A → aA / Φ
S = { S }
T = { a, b }
V = { S, A }
Q : It starting start with a and end with b or start with b and end with a.
L = { a(a+b)ⁿb U b(a+b)ⁿa}
S → aAb/bAa
A → aA / bA / ε
S = { S }
T = { a, b }
V = { S, A }
Q : Write a language over {a, b, c} all the string that contain abc as prefix and cba as suffix.
L = { abc (a+b+c)ⁿ bca | n≥0 }
Q : Write a language over {a, b, c} all the string that contain ‘aba’ is present starting side & ‘cba’ is end side of string.
{ (a+b+c)ⁿ aba (a+b+c)ⁿ cba (a+b+c)ⁿ | n, m, p≥0}
L = { abc (a+b+c)ⁿ cba | n≥0 }
S = abc ab cba
S ∈ L ( Yes / No )
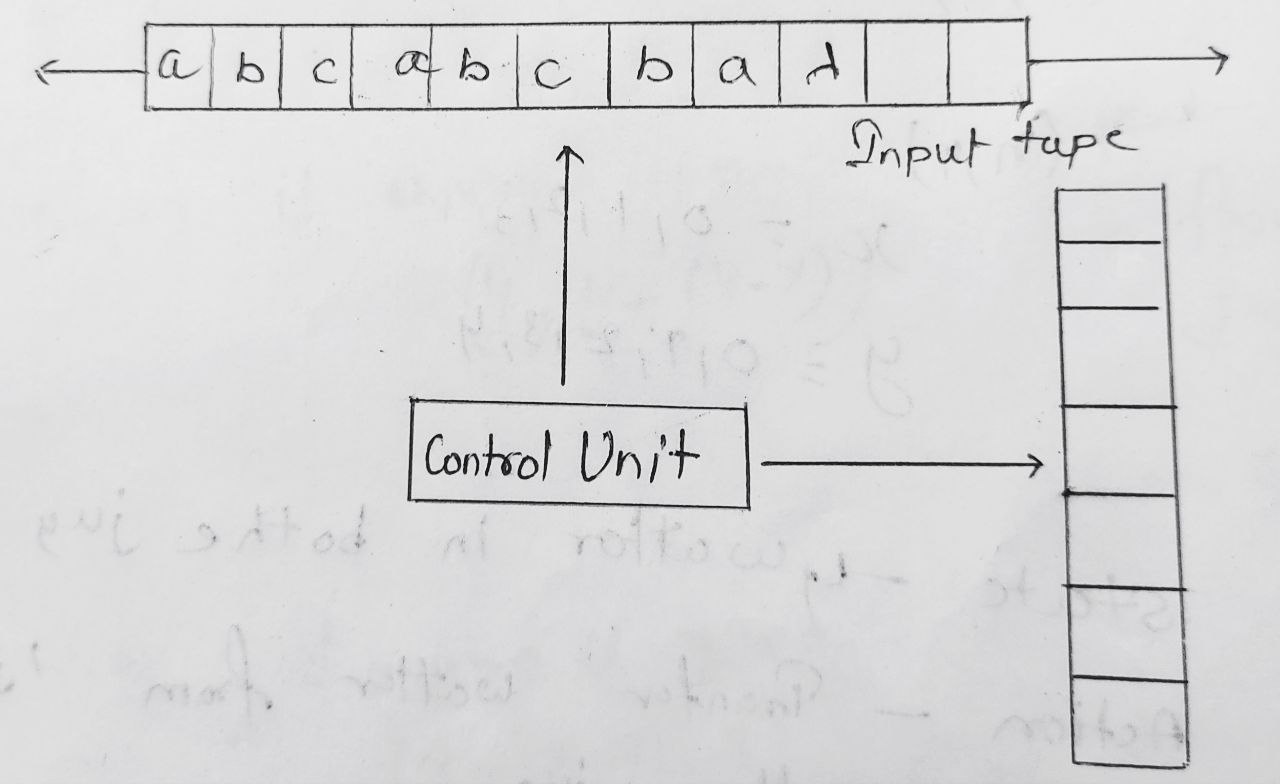
Σ = { 2, 4, 5}
Input String = { 2, 4,2, 4, 5 ,4 ,2 ,5 }
(No of State) Q * Σ → Q (Next output State)
[1, 2] → 2
[2, 4] → 5
[5, 2] → F
Note : Input String should be consume
-
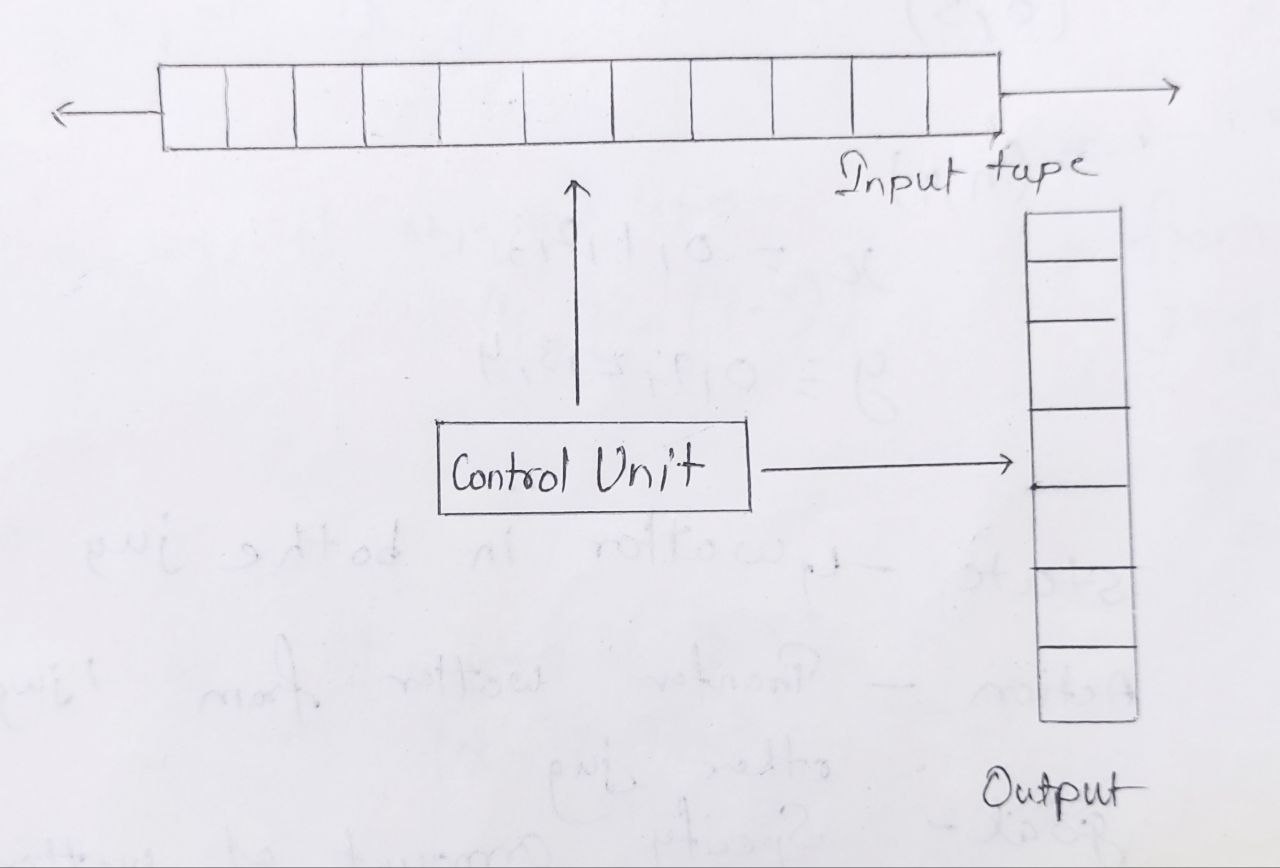
M : Finite automata
-
Q : Finite set of states
-
Σ : Finite set of input symbol
-
δ : Transition function (Give us the next state)
-
q₀ : Starting state
-
F : Finite set of final state
-
Representation
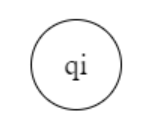
States representation
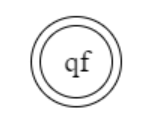
Representation of final state
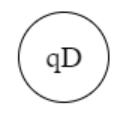
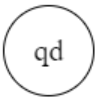
Dead state
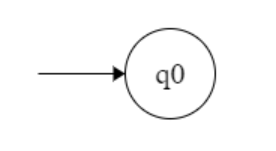
Representation of starting state
Transition function
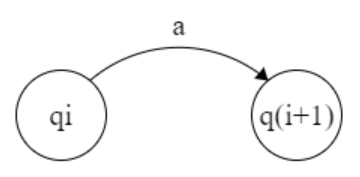
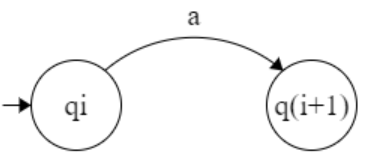
δ : Q * Σ → Q
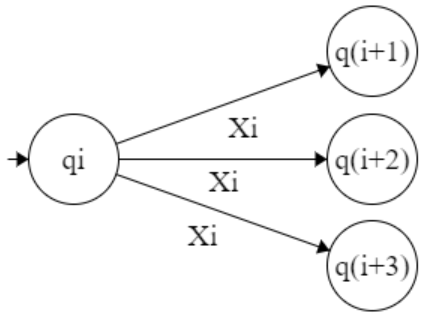
δ ( qᵢ , a) → qᵢ₊₁
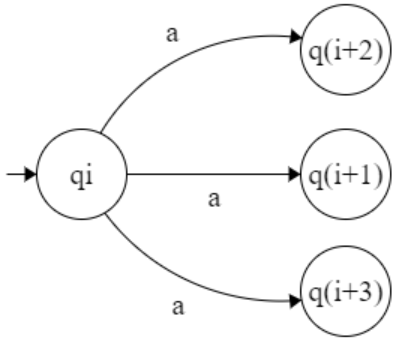
Deterministic
Non-Deterministic
-
Example
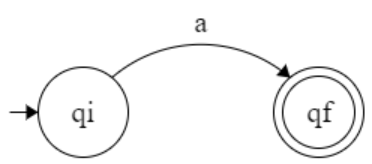
L = { a }
Σ = { a }
Finite automata check the given string is belong to given language or not.
Q = { q₀ , qf }
Σ = { a }
δ : ( q₀ , a) → qf
q₀ = q₀
F = { qf }
-
Complete DFA
Q = { q0, qf, qD }
Σ = { a }
δ : ( q0, a ) → qf
δ : ( qf, a ) → qD
δ : ( qD, a ) → qD
q0 = q0
F = { qf }
-
Transition Table
State
Input
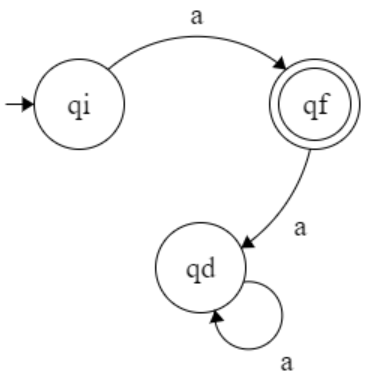
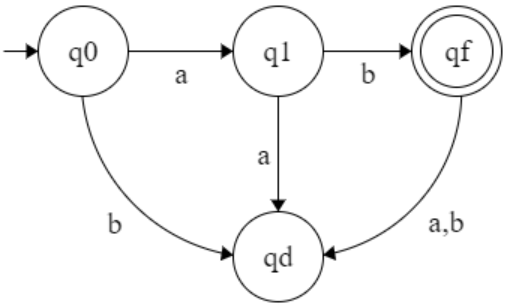
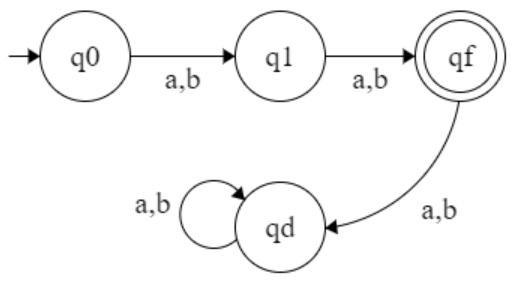
L = { a b}
q0 = q0
F = { qf }
Σ = { a, b }
Q= { q0, q1, qf, qd}
S : ( q0, a) → q1
S : ( q0, b) → qd
S : ( q1, a) → qd
S : ( q1, b) → qf
S : ( qf, a or b) → qd
S : ( qd, a or b ) → qd
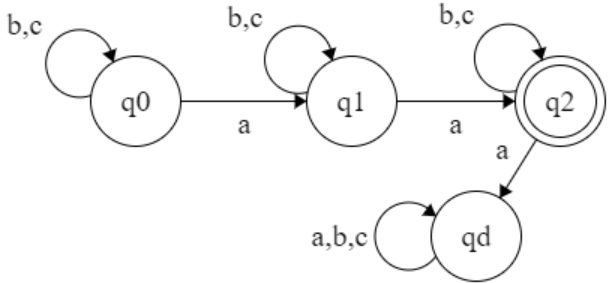
L = { (a + b)ⁿ | n=2 } Σ = { a, b }
L = { aa, bb, ab, ba }
Q = { q0, q1, qf, qd }
S : ( q0, a) → q1
S : ( q0, b) → q1
S : ( q1, a/b) → qf
S : ( qf , a/b) → qd
S : ( qd, a/b) → qd
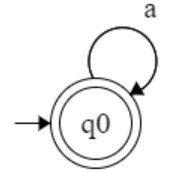
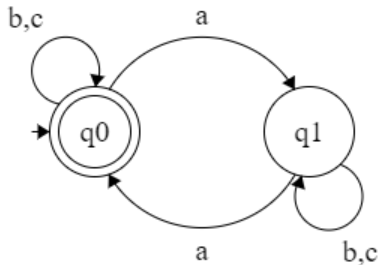
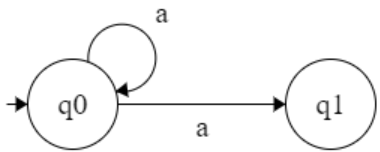
L = { aⁿ | n≥0 }
Q = { q0 }
S : ( q0 , a ) → q0
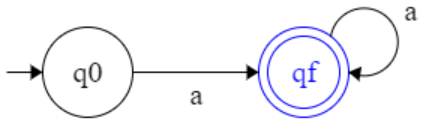
L = { aⁿ | n >1 }
Q = { q0 , qf }
S : ( q0 , a ) → qf
S : ( qf , a ) → qf
L = { (a + b)ⁿ | n > 2 }
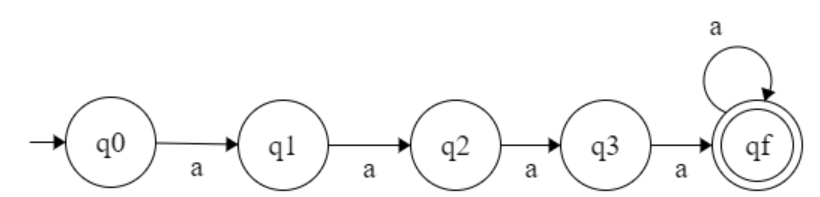
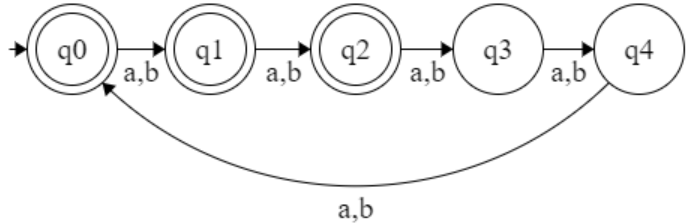
L = { aⁿ | n > 3 }
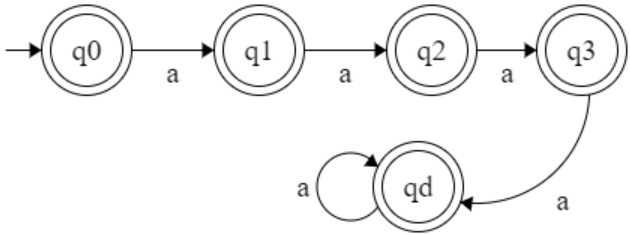
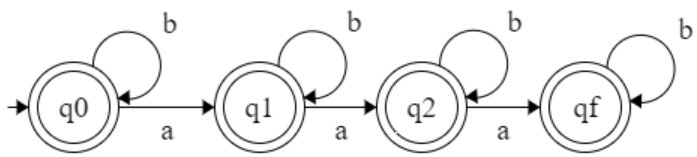
L = { aⁿ | n ≤ 3 }
Q = { q0, q1, q2, q3, qD }
F = { q0, q1, q2, q3, qD }
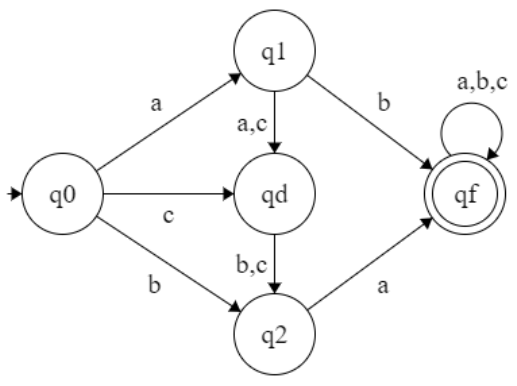
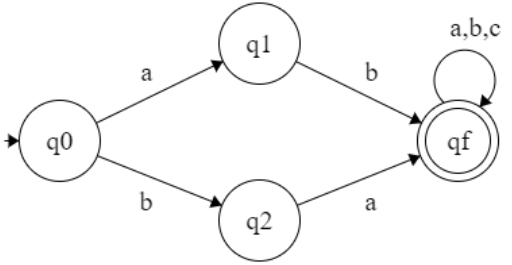
L = { All strings over {a, b, c} that start with ab or bc }
L = { ab(a + b) U bc(a + b) }
Design a finite automata for language L={ aⁿbⁿ | n ≥ 0 }
This is not possible with finite automata
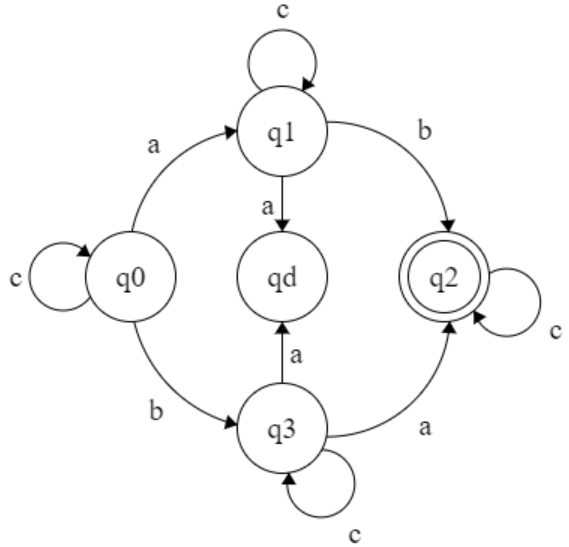
L = { A language that contain exactly 2 a’s } Σ = { a, b, c }
L = { (b+c)ⁿ a (b+c)ᵐ a (b+c)ᵖ | n, m, p ≥ 0 }
Exactly one a and one b
L = { cⁿ a cᵐ b cᵖ U cⁿ b cᵐ a cᵖ | n,m,p≥0 }
Design a DFA all over { a, b } , { a, b, c }
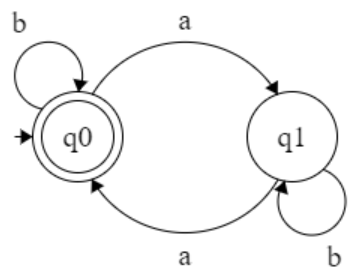
L = { All the string even no of a }
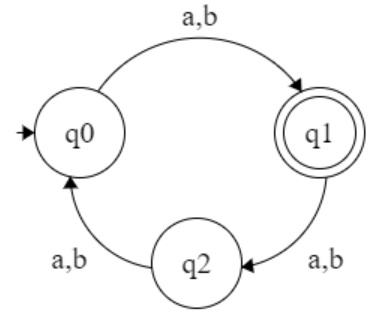
L = { bⁿ aʳ bᵐ aᵉ bᵖ | n, m, p ≥0 & (r + e) =2x ,x ≥ 0 } Σ = { a, b }L = { (c+b)ⁿ aʳ (b+c)ᵐ aᵉ (b+c)ᵖ | n, m, p ≥0 & (r + e) =2x ,x ≥ 0 } Σ = { a, b, c }
L = { w | w ∈ (a + b) }*
i) Language contain all the language had last 3rd position is b
ii) From the left the 2nd position will be ‘a’ and 4th position from the right will be ‘b’
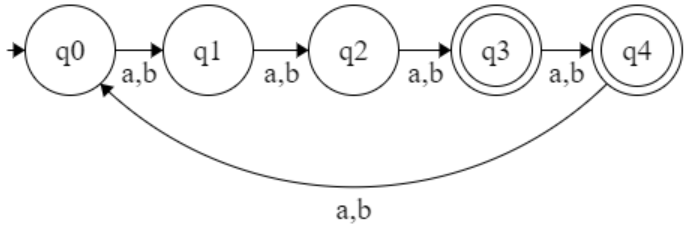
iii) L = { w | w ∈ (a + b) and |w| mod 3 = 1 }* |w| : length of the string
L = { a, b , aaaa, bbbb, abab, baba ,….. }
| w | mod n = k ( Where n = no of states, k = final state )
iv) L = { w | w ∈ (a + b) }*
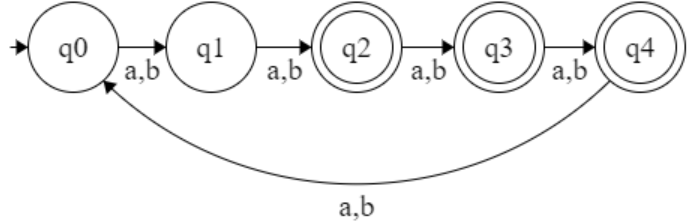
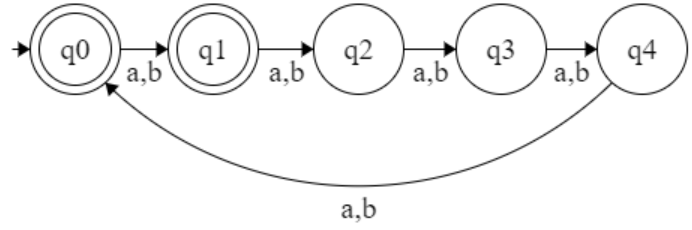
| w | mod 5 > 2
| w | mod 5 ≥ 2
| w | mod 5 < 2
| w | mod 5 ≤ 2
Σ = { a, b }
L = { w | w ∈ (a + b) and No ‘a’ mod 3 > No ‘b’ mod 3 }*
for mod of 3 we get { 0, 1, 2 }
No ‘a’ mod 3 > No ‘b’ mod 3 1 1 Reject 0 0 Reject 2 2 Reject 0 1 Reject 0 2 Reject 1 2 Reject 1 0 Accept 2 0 Accept 2 1 Accept -
Regular Language : A regular language is a language for which there exists at least one finite automata that will accept all the strings of the language.
Regular Expression : It is a specific arrangement of notation through which we can generate the entire set of strings.
Regular Set : The set which generated by Regular Expression.
-
∅ = { } ( empty set )
-
λ = { λ } ( null set )
-
a ∈ Σ then a is Regular Expression.
-
a, b ∈ Σ then (a + b) is a Regular Expression
Regular Language → L = { a, b }
-
a, b ∈ Σ then ( a.b ) is a Regular Expression
Regular Language → L = { ab }
-
a ∈ Σ then a* is a Regular Expression.
-
a ∈ Σ then a⁺ is a Regular Expression.
-
r1 and r2 is a regular expression then
( r1+r2 ) → R.E
( r1.r2 ) → R.E
( r1 )* → R.E
( r1 ) → R.E
( r1 )* + ( r1 + r2 ) → R.E
- Question :
-
L = { a }
a → R.E
-
L= { a, b }
( a + b) → R.E
-
L = { aa, ab, bb, ba }
( a+b )( a+b ) → R.E
-
L = { a, aa, aaa }
( a + aa + aaa ) → R.E
-
L = { w | w contains ‘ab’ as a prefix and w ∈ Σ } and Σ = { a, b}
(ab (a + b)* ) → R.E
-
L = { w | a ∈ Σ and w start and end with different symbol } and Σ = { a, b}
( a ( a+b )* b) + ( b (a+b)* a) → R.E
-
If atleast one ‘a’ come at start then one ‘b’ come at end or atleast one ‘b’ come at start then one ‘a’ come at end
(a+b)* ((a (a+b)* b) + (b (a+b)* a)) (a+b)* → R.E
-
L = { w | w contains even no of a’s } and Σ = { a }
L = { λ, aa, aaaa, ….. }
R.E → (aa)*
-
L = { w | w contains odd no of a’s } and Σ = { a }
L = { a, aaa, aaaaa, ….. }
R.E → a(aa)*
-
- Regular languages are closed under the following operations:
-
Union Operation
L1 = { w | w contains even no of a’s }
L2 = { w | w contains odd no of a’s }
L1 = (aa)*
L2 = a(aa)*
L1 U L2 = (aa)* + a(aa)*
L1 U L2 = { λ, aa, aaaa, ….. , a, aaa, aaaaa, ….. }
L1 U L2 = a*
-
Intersection Operation
L1 = { aⁿ | n≥0 }
L2 = { aᵐ | m≥ even no }
L1 ∩ L2 = R.L
L1 = { λ, a, aa, aaa, aaaa, …. }
L2 = { λ, aa, aaaa, aaaaaa, ….. }
L1 ∩ L2 = { λ, aa, aaaa, aaaaaa, …. } = (aa)*
-
Concatenation
L1 = { aⁿ | n≥0 }
L2 = { bᵐ | m≥0 }
L1L2 = { aⁿbᵐ | n,m≥0 }
-
Replication
L1 = { aⁿ | n≥0 }
L1 = { λ, a, aa, aaa, aaaa, …. }
L1* = { λ*, a*, aa*, aaa*, aaaa*, …. }
L1* = { λ, ( a, aa, aaa,… ), ( aa, aaaa, aaaaaa,… ), (aaa, aaaaaa,…. ) , ……. }
L1* = { λ, a, aa, aaa, aaaa, …. }
L1* = L1 = a*
-
Complement
L1 = { w | w ∈ a* and w is even number of a’s }
L2 = { w | w ∈ a* } = U ( universal set )
L1 = { λ, aa, aaaa, aaaaaa, ….. }
L2 = { λ, a, aa, aaa, aaaa, …. }
L2 - L1 = { a, aaa, aaaaa, …. }
check L1’ = ( R or Not ) = L2 - L1 = a* - (aa)*
a(aa)* = L1’
-
-
Regular Grammar
$G = <T, V, S, P>$ is said to be regular grammar if all the production are in the form of :A → xB
A → Bx
A → x
( Right Linear G )
( Left Linear G )
Where A and B ∈ V
x ∈ T*-
Example :
i ) L = {a}
S → a
S = {S}
T = {a}
V = {S}
P : S → a
iii ) (aa)*
S → aaS/∈
or S → aaS | S → ∈
or S → Saa | S → ∈
S = {S}
T = {a, ∈}
V = {S}
Vii ) L = { a, ab, aa, aab, aba ,abb, …. }
R.E = a(a+b)*
S → aA
A → aA/bA/∈
ix ) Language having a in 3rd position always from the start.
R.E = (a+b)(a+b)a(a+b)*
S → aaaA
S → abaA
S → baaA
S → bbaA
A → aA/bA/∈
ii ) L = a*
S → aS/∈ or S → aS | S → ∈
S = {S}
T = {a, ∈}
V = {S}
P : S → aS | P : S → ∈
iv ) a(aa)*
S → aaS/a
or S → aaS | S → a
v ) ab
S → aS/A/∈
A → bA/∈
viii ) L = Contain all the string over a and b , aba as suffix
R.E = (a+b)*aba
S → Aaba
A → aA/bA/∈
-
(qi, xi)
δ : ( q0, a) →
No state { }
{ q0 }
{ q1 }
{ q0, q1 }
{ { }, { q0 }, { q1 }, { q0, q1 } } → power set
-
Example :
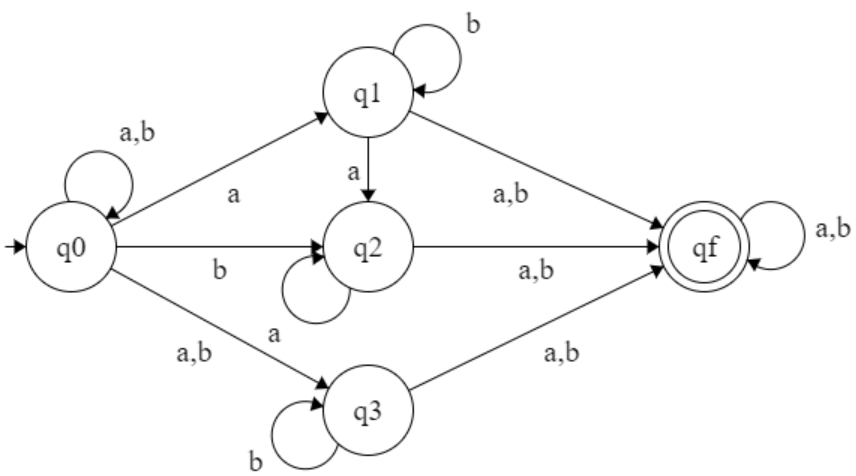
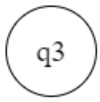
Q = { q0, q1, q2, q3, qf }
q0 = { q0 }
F = { qf }
Σ = { a, b }
Transition Function : -
δ : ( q0, a ) = { q0, q1, q3 }
δ : ( q0, b) = { q0, q2, q3 }
δ : ( q1, a ) = { q2, qf }
δ : ( q1, b ) = { q1, qf }
Transition Table : -
Q
a
{ q0, q1, q3 }
{ q2, qf }
{ q2, qf }
{ qf }
{ qf }
b
{ q0, q2, q3 }
{ q1, qf }
{ qf }
{ q3, qf }
{ qf }
-
Question :
-
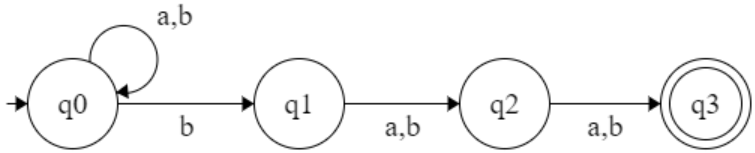
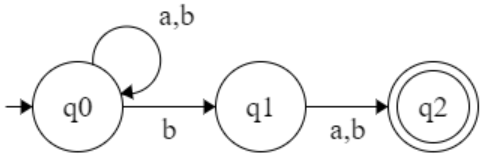
L = { w | w having b at third last position }
R.E = (a+b)* b (a+b) (a+b)
-
a ( a+b ) b*
-
( a+b ) a ( a+b ) b ( a+b )***
-
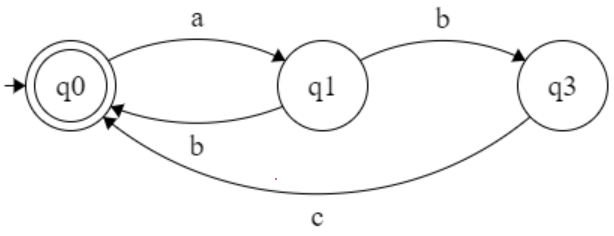
R.E = (ab+abc)*
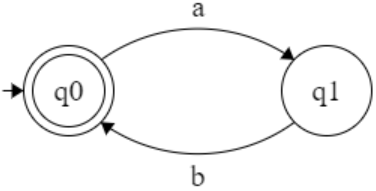
(ab)*
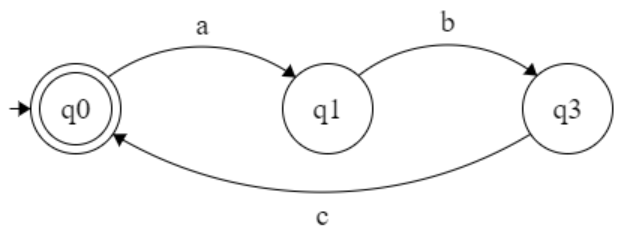
(abc)*
-
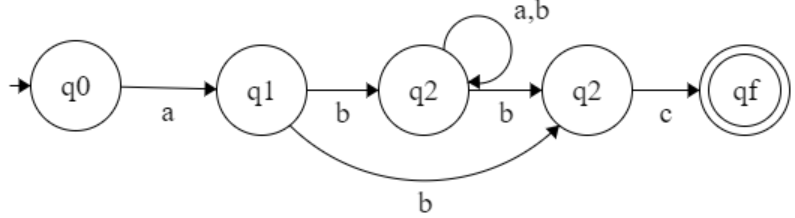
L = { w | w having ab at staring and bc at the end }
R.E = ( ab ( a+b+c )* bc + abc )
-
L = { w | w having maximum 3 a’s }
R.E = b* + (ba b) + (ba ba b*) + (ba ba ba b)
-
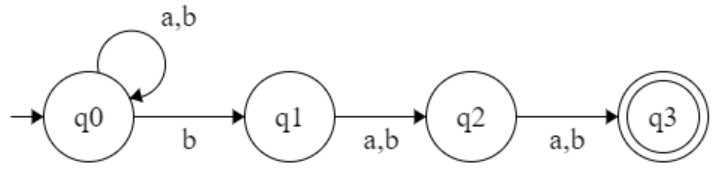
L = { w | w having last 5th position a and last 3rd position b }
R.E = (a+b)* a (a+b) b (a+b) (a+b)
-
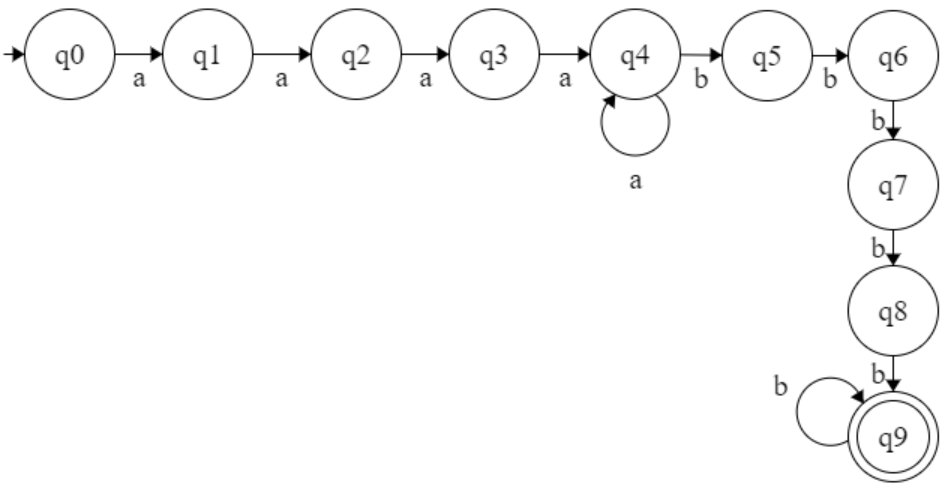
L = { aⁿbᵐ | n>3 m>4 }
-
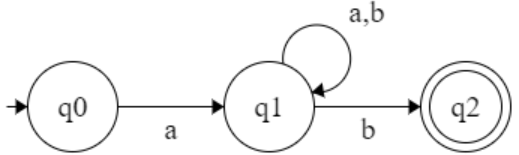
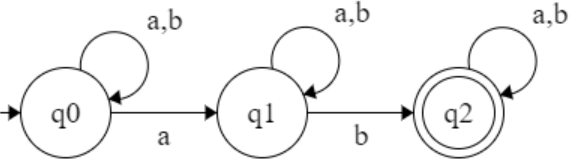
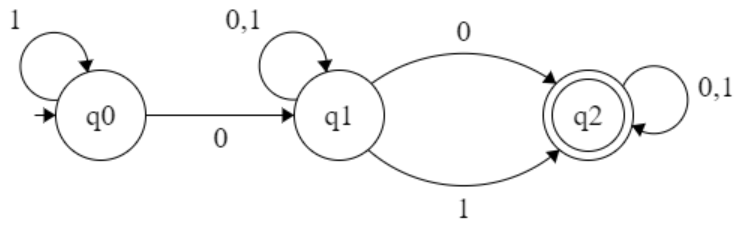
Q = { q0, q1, q2 }
Σ = { 0, 1}
q0 = q0
F = { q2 }
Transition Table :
States
Input
0
{ q1 }
{ q1, q2 }
{ q2 }
1
{ q0 }
{ q1, q2 }
{ q2 }
DFA equibalance to M
Σ’ = Σ
Q’ = { }
q0’ = q0
-
Step 1 ⇒ Add q0 to Q’
Q’ = { q0 }
for this q0’ = q0
-
Step 2 ⇒ Find the transition of q0
δ’ : ( q0, 0 ) → {q1}
δ’ : ( q0, 1 ) → {q0}
q1 is not in Q’
Add q1 in Q’
for this Q’ = { q0, q1 }
-
Step 3 ⇒ Find the transition for q1
δ’ : ( q1, 0 ) → {q1, q2}
δ’ : ( q1, 1 ) → {q1}
now, Q’ = {q0, q1, {q1, q2}}
-
Step 4 ⇒ Find transition for {q1, q2}
δ’ : ( {q1, q2}, 0 ) → δ’:(q1, 0) U δ’:(q2,0)
{q1,q2} U {q2} ⇒ {q1,q2}δ’ : ( {q1, q2}, 1 ) → δ’:(q1, 1) U δ’:(q2, 1)
{q1} U {q2,q2} ⇒ {q1,q2}There is no new state.
All the state that contains final state of NFA will be the final state of DFA.
For this Final State in NFA q2 so in DFA Final State F’ = {q1, q2}
Transition Table :
Q’
{q0}
{q1}
{q1, q2}
{q2}
0
{q1}
{q1, q2}
{q2}
{q2}
1
{q0}
{q1}
{q1, q2}
{q1, q2}
At {q2} there is no incoming arrow from other state so this is unreadable state (we can remove this)
-
Question :
(a+b)* b (a+b)
δ’ : ( q0, a ) → {q0}
δ’ : ( q0, b ) → {q0, q1}
δ’ : ( {q0,q1}, a ) → δ’ : ( q0, a ) U δ’ : ( q1, a ) → { q0, q2 }
δ’ : ( {q0,q1}, b ) → δ’ : ( q0, b ) U δ’ : ( q1, b ) → { q0, q1, q2 }
δ’ : ( {q0,q2}, a ) → δ’ : ( q0, a ) U δ’ : ( q2, a ) → { q0 }
δ’ : ( {q0,q2}, b ) → δ’ : ( q0, b ) U δ’ : ( q2, b ) → { q0, q1}
δ’ : ( {q0, q1, q2}, a ) → δ’ : ( q0, a ) U δ’ : ( q1, a ) U δ’ : ( q2, a ) → { q0, q2 }
δ’ : ( {q0, q1, q2}, b ) → δ’ : ( q0, b ) U δ’ : ( q1, b ) U δ’ : ( q2, b ) → { q0, q1, q2 }
Now the states are {q0} ,{ q0,q1}, {q0,q2}, {q0, q1, q2}
because q2 was the final state then in DFA final states are {q0, q2}, {q0, q1, q2}
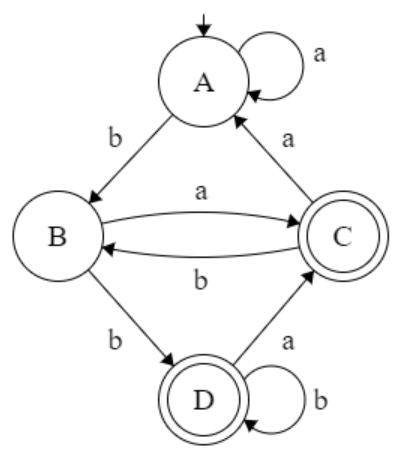
Transition Table :
Name
A
B
C
D
Q’
{q0}
{q0,q1}
{q0,q2}
{q0, q1, q2}
a
{q0}
{q0,q2}
{q0}
{q0,q2}
b
{q0,q1}
{q0, q1, q2}
{ q0, q1}
{q0,q1,q2}
Number of unreachable state - 2 states are q1 and q2.
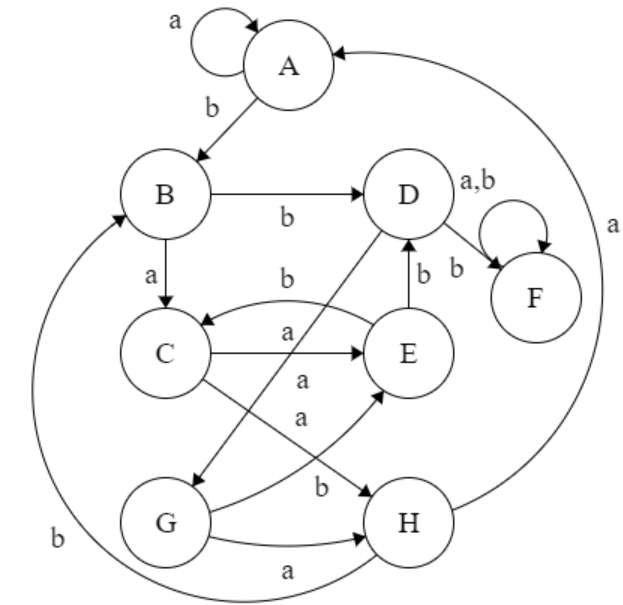
Transition Table :
Name
A
B
C
D
E
F
G
H
Q
{q0}
{q0,q1}
{q0,q2}
{q0,q1,q2}
{q0,q1,q3}
{q0,q1,q2,q3}
{q0,q2,q3}
{q0,q3}
a
{q0}
{q0,q2}
{q0,q3}
{q0,q2,q3}
{q0,q2}
{q0,q1,q2,q3}
{q0,q3}
{q0}
b
{q0,q1}
{q0,q1,q2}
{q0,q1,q3}
{q0,q1,q2,q3}
{q0,q1,q2}
{q0,q1,q2,q3}
{q0,q1,q3}
{q0,q1}
-
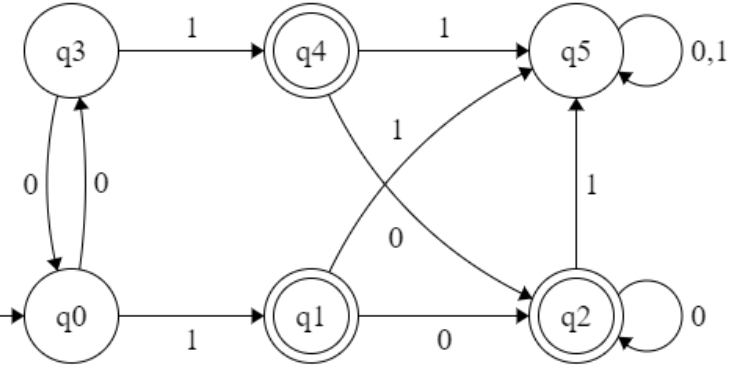
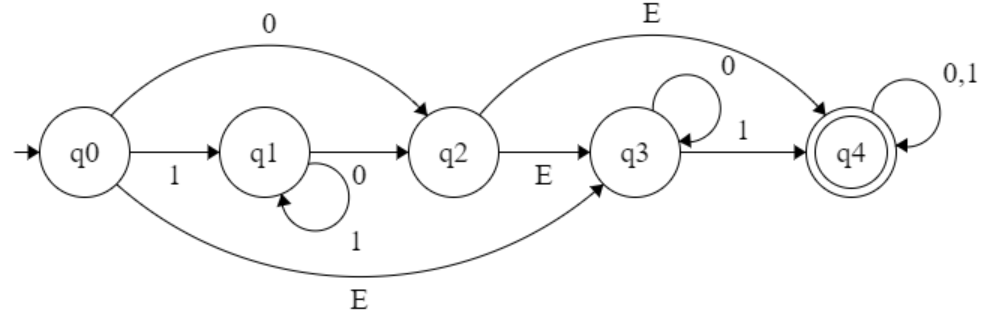
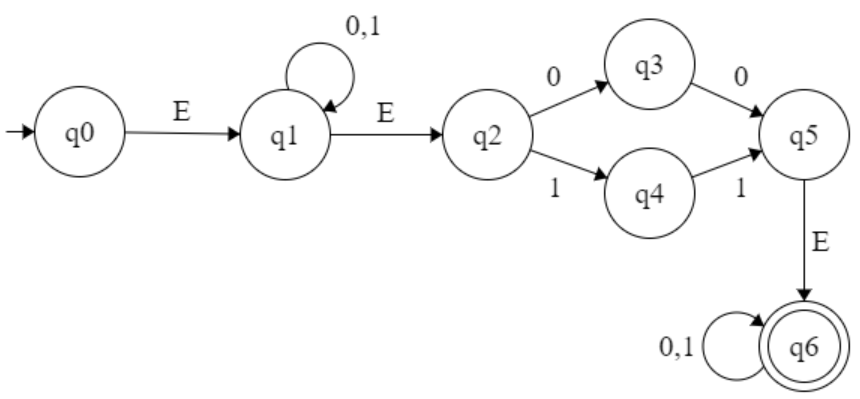
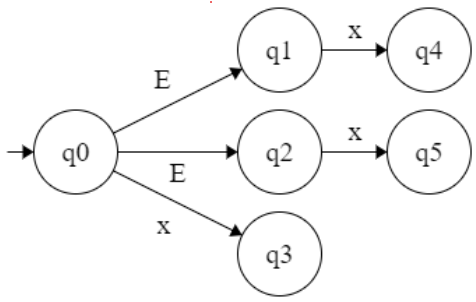
Example :
∈ - closer of q0 : {q0,q3}
∈ - closer of q3 : {q3}
∈ - closer of q1 : {q1}
∈ - closer of q4 : {q4}
∈ - closer of q2 : {q2,q3,q4}
-
Representation :
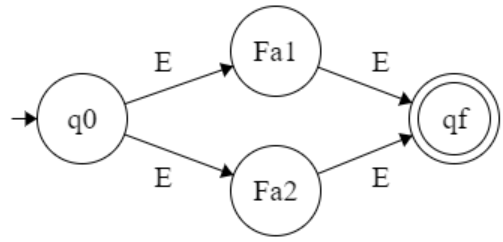
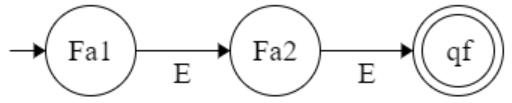
r1 and r2 are two regular expression
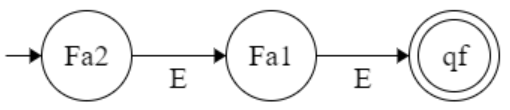
Change from ∈ - NFA to NFA, Initial State, Final State and Number of state are same as ∈-NFA.
∈-NFA : M = ( Q, Σ, δ, q₀, F )
NFA : M’ = ( Q’, Σ’, δ’, q₀’, F’ )
Σ’ = Σ | Q’ = Q | q0’ = q0 | F’ = F | δ : (qi , x) ⇒ ∈ (δ : ( ∈-closer(qi), x))
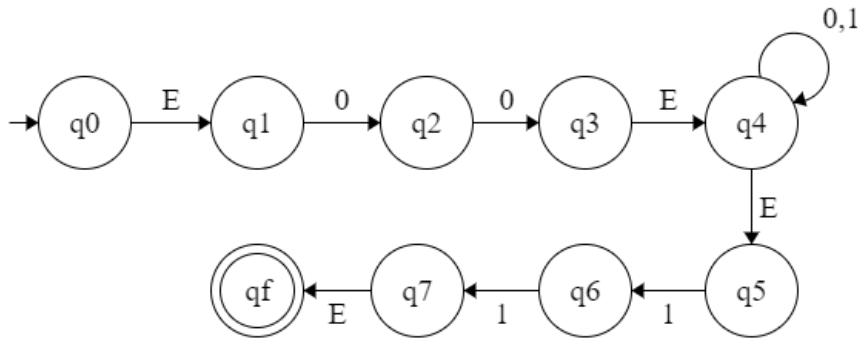
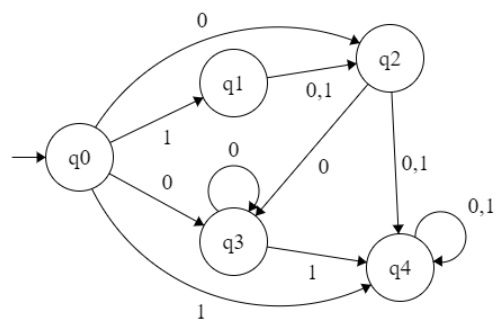
∈(q0) = { q0,q1,q2 } (∈-closer of q0)
Transition Function :
δ:( q0, 0 )→ ∈ closer(δ:(∈ closer(q0),0))→ ∈ closer(δ:( {q0,q3},0))→ ∈ closer(δ:(({q0}, 0) U ({q3}, 0)))→ ∈ closer({q2}U{q3})⇒ {q2,q3,q4}
δ:( q0, 1 )→ ∈ closer(δ:( ∈ closer(q0), 1))→ ∈ closer(δ:( {q0,q3}, 1))→ ∈ closer(δ:(({q0}, 1) U ({q3}, 1)))→ ∈ closer({q1}U{q4}) ⇒ {q1,q4}
δ:( q1, 0 )→ ∈ closer(δ:( ∈ closer(q1), 0))→ ∈ closer(δ:( {q1}, 0 )) → ∈ closer{q2} ⇒ {q2,q3,q4}
δ:( q1, 1 )→ ∈ closer(δ:( ∈ closer(q1), 1))→ ∈ closer(δ:( {q1}, 1))→ ∈ closer{q2} ⇒ {q2,q3,q4}
δ:( q2, 0 )→ ∈ closer(δ:( ∈ closer(q2), 0))→ ∈ closer(δ:( {q3,q4}, 0))→ ∈ closer(δ:(({q3}, 0) U ({q4}, 0)))→ ∈ closer({q3}U{q4}) ⇒ {q3,q4}
δ:( q2, 1 )→ ∈ closer(δ:( ∈ closer(q2), 1))→ ∈ closer(δ:( {q3,q4}, 1))→ ∈ closer(δ:(({q3}, 1) U ({q4}, 1)))→ ∈ closer({q4}U{q4})⇒ {q4}
δ:( q3, 0 )→ ∈ closer(δ:( ∈ closer(q3), 0))→ ∈ closer(δ:( {q3}, 0)) ⇒ {q3}
δ:( q3, 1 )→ ∈ closer(δ:( ∈ closer(q3), 1))→ ∈ closer(δ:( {q3}, 1)) → ∈ closer({q4}) ⇒ q4
δ:( q4, 0 )→ ∈ closer(δ:( ∈ closer(q4), 0))→ ∈ closer(δ:( {q4}, 0)) ⇒ {q4}
δ:( q4, 1 )→ ∈ closer(δ:( ∈ closer(q4), 1))→ ∈ closer(δ:( {q4}, 1)) ⇒ {q4}
-
Question : 1.
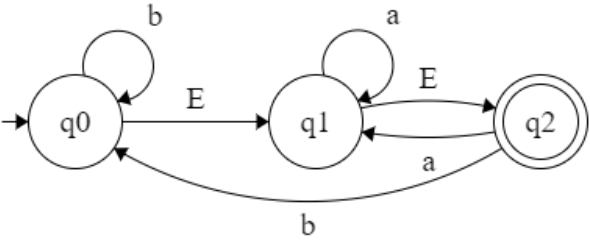
 ∈(q0)={q0,q1} ∈(q1)={q1} ∈(q2)={q2} ∈(q3)={q1,q2,q3} **∈-NFA : M = ( Q, Σ, δ, q₀, F )** **NFA : M’ = ( Q’, Σ’, δ’, q₀’, F’ )** Q’ = Q Σ’=Σ q₀’=q₀ F’ = F={{q2},{q3}} δ’:(q0, 0)→ ∈(δ’:(∈(q0), 0))→ ∈(δ’:({q0,q1}, 0))→ ∈(δ’:(({q0}, 0)U({q1}, 0))→ ∈({q0})U∈({q3})→ {q0,q1}U{q1,q2,q3} ⇒ {q0,q1,q2,q3} δ’:(q1, 0)→ ∈(δ’:(∈(q1), 0))→ ∈(δ’:({q1}, 0))→ ∈({q3}) ⇒ {q1,q2,q3} δ’:(q1, 1)→ ∈(δ’:(∈(q1), 1))→ ∈(δ’:({q1}, 1))→ ∈(q2) ⇒ {q2} δ’:(q2, 0)→ ∈(δ’:(∈(q2), 0))→ ∈(δ’:({q2}, 0))→ ∈({q2}) ⇒ {q2} δ’:(q2, 1)→ ∈(δ’:(∈(q2), 0))→ ∈(δ’:({q2}, 0)) ⇒ {q2} δ’:(q3, 0)→ ∈(δ’:(∈(q3), 0))→ ∈(δ’:({q1,q2,q3}, 0))→ ∈(δ’:(({q1},0)U({q2},0)U({q3}, 0))) → ∈({q3})U∈({q2})U{} ⇒ {q1,q2,q3} δ’:(q3, 1)→ ∈(δ’:(∈(q3), 1))→ ∈(δ’:({q1,q3}, 1))→ ∈(δ’:({q1},1) U ({q3},1))→ (∈({q2})U{} ⇒ {q2}  ----
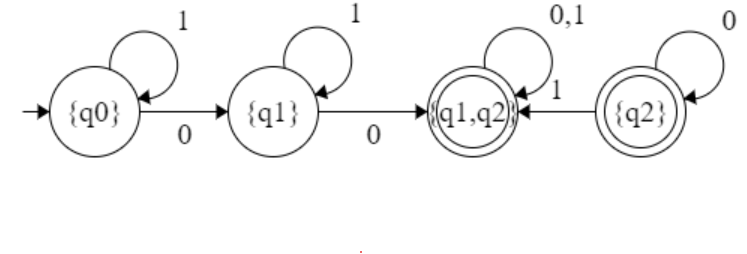
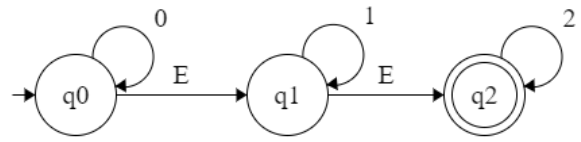
δ’:(q0, 0)→ ∈(δ’:(∈(q0), 0))→ ∈(δ’:({q0,q1,q2}, 0))→ ∈(δ’:(({q0}, 0)U({q1}, 0)U({q2}, 0))→ ∈({q0}) ⇒ {q0,q1,q2}
δ’:(q0, 1)→ ∈(δ’:(∈(q0), 1))→ ∈(δ’:({q0,q1,q2}, 1))→ ∈(δ’:(({q0}, 1)U({q1}, 1)U({q2}, 1))→ ∈({q1}) ⇒ {q1,q2}
δ’:(q0, 2)→ ∈(δ’:(∈(q0), 2))→ ∈(δ’:({q0,q1,q2}, 2))→ ∈(δ’:(({q0}, 2)U({q1}, 2)U({q2}, 2))→ ∈({q2}) ⇒ {q2}
δ’:(q1, 0)→ ∈(δ’:(∈(q1), 0))→ ∈(δ’:({q1,q2}, 0))→ ∈(δ’:(({q1}, 0)U({q2}, 0))→ ∈({}) ⇒ {}
δ’:(q1, 1)→ ∈(δ’:(∈(q1), 1))→ ∈(δ’:({q1,q2}, 1))→ ∈(δ’:(({q1}, 1)U({q2}, 1))→ ∈({q1}) ⇒ {q1,q2}
δ’:(q1, 2)→ ∈(δ’:(∈(q1), 2))→ ∈(δ’:({q1,q2}, 2))→ ∈(δ’:((q1, 2)U({q2}, 2))→ ∈({q2}) ⇒ {q2}
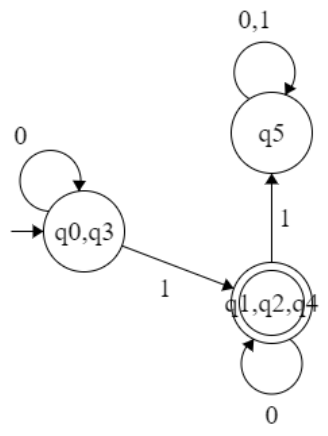
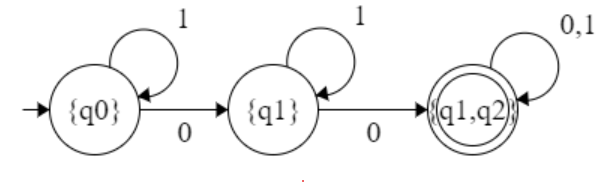
δ’:(q2, 2)→ ∈(δ’:(∈(q2), 2))→ ∈(δ’:({q2}, 2))→ ∈(δ’:(({q2}, 2))→ ∈({q2}) ⇒ {q2} ∈ - NFA to DFA
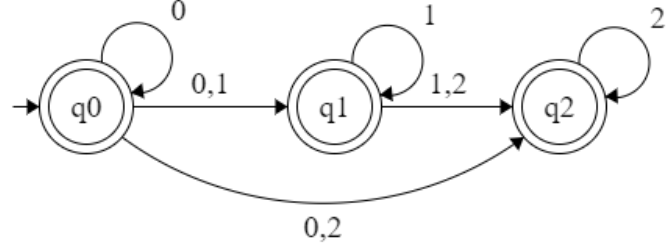
∈(q0)={q0,q1,q2}
∈(q1)={q1,q2}
∈(q2)={q2}
∈-NFA : M = ( Q, Σ, δ, q₀, F )
NFA : M’ = ( Q’, Σ’, δ’, q₀’, F’ )
Σ’=Σ
Q’={ }
q0’=∈-closer(q0)
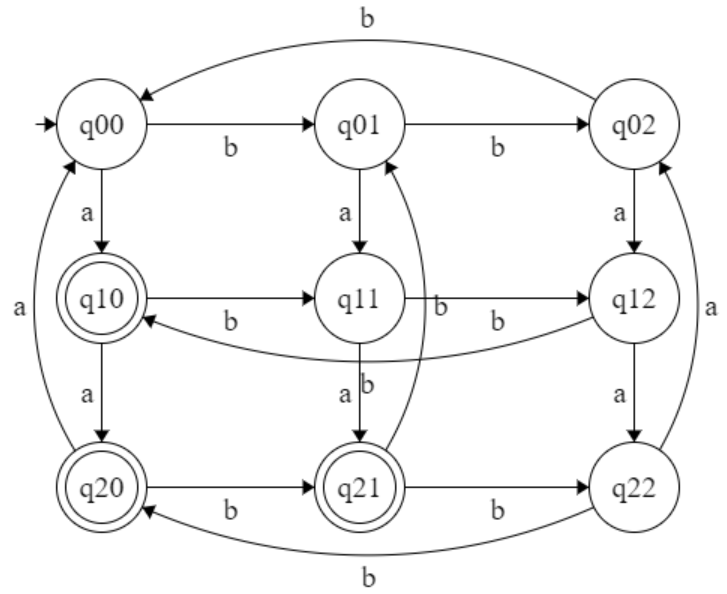
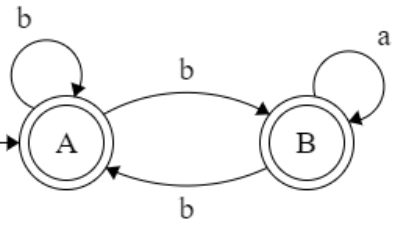
q0={q0,q1,q2}=A
δ’ : (A, a) ⇒ ∈(δ’:( A, a)) ⇒ ∈(δ’:( {q0,q1,q2}, a)) ⇒
∈(δ’:( (q0, a) U (q1,a) U (q2,a) )) ⇒ ∈({}U{q1}U{q1}) ⇒ ∈(q1) ⇒ {q1,q2} = B
δ’ : (A, b) ⇒ ∈(δ’:( A, b)) ⇒ ∈(δ’:( {q0,q1,q2}, b)) ⇒
∈(δ’:( (q0,b) U (q1,b) U (q2,b) )) ⇒ ∈({q0}U{}U{q0}) ⇒ ∈(q0) ⇒ {q0,q1,q2} = A
δ’ : (B, a) ⇒ ∈(δ’:( B, a)) ⇒ ∈(δ’:( {q1,q2}, a)) ⇒ ∈(δ’:( (q1,a) U (q2,a) )) ⇒ ∈({q1}U{q1}) ⇒ ∈(q1) ⇒ {q1,q2} = B
δ’ : (B, b) ⇒ ∈(δ’:( B, b)) ⇒ ∈(δ’:( {q1,q2}, b)) ⇒ ∈(δ’:((q1,b) U (q2,b)) ⇒ ∈({}U{q1}) ⇒ ∈(q0) ⇒ {q0,q1,q2} = A
All the state which have q2 is final state
-
-
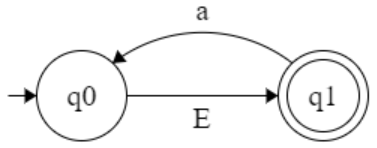
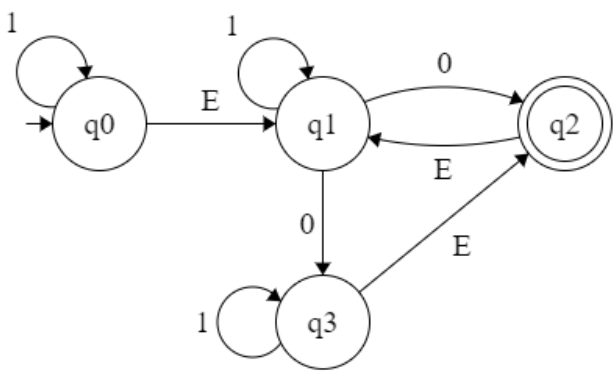
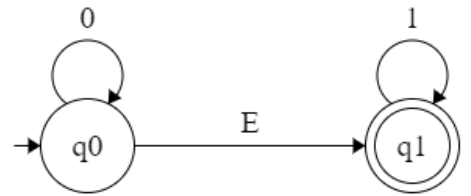
q0 = {q0,q1} = A
δ’ : (A, 0)
δ’ : (A, 1)
δ’ : (B, 1)
δ’ : (B, 0)
= ∈(δ’:( {q0,q1}, 0))
= ∈(δ’:((q0, 0)U(q1,0))
= ∈({}U{q2,q3})
= ∈(q2,q3) = {q1,q2,q3} = B
= ∈(δ’:( {q0,q1}, 1))
= ∈(δ’:((q0, 1)U(q1, 1))
= ∈({q0}U{q1})
= ∈(q0,q1) = {q0,q1} = A
= ∈(δ’:( {q1,q2,q3}, 1))
= ∈(δ’:((q1, 1)U(q2, 1)U(q3,1))
= ∈({q1}U{}U{q3})
= ∈(q1,q3) = {q1,q2,q3} = B
= ∈(δ’:( {q1,q2,q3}, 0))
= ∈(δ’:((q1, 0)U(q2, 0)U(q3,0))
= ∈({q2}U{}U{q3})
= ∈(q2,q3) = {q1,q2,q3} = B
-
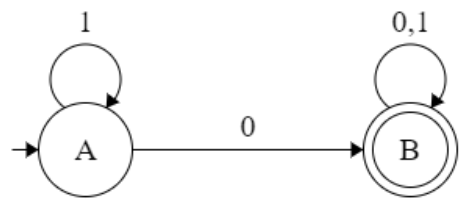
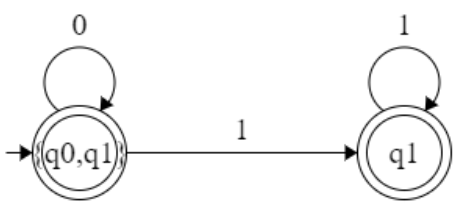
q0’ = {q0,q1} =A
δ’ : (A, 0)
δ’ : (A, 1)
δ’ : (q1, 0)
δ’ : (q1, 1)
= ∈(δ’:({q0,q1}, 0))
= ∈(δ’:((q0, 0)U(q1,0))
= ∈(q0) = {q0,q1} = A
= ∈(δ’:({q0,q1}, 1))
= ∈(δ’:((q0, 1)U(q1,1))
= ∈(q1) = {q1}
= ∈(δ’:({q1}, 0))
= ∈({}) ={}
= ∈(δ’:({q1}, 1))
= ∈({q1}) ={q1}
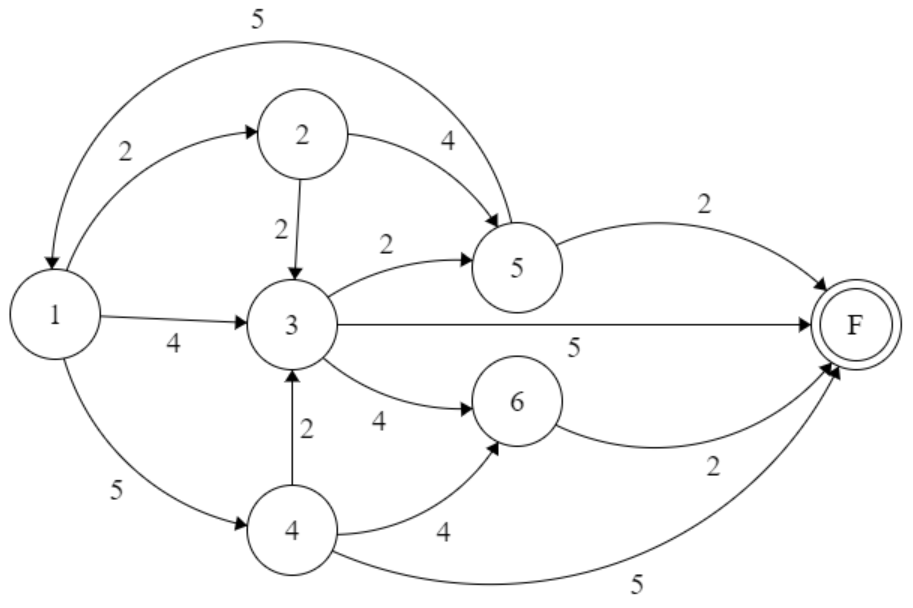
Zero equivalence(k=0) :
P0 = {{ q0, q3, q5}, {q1, q2, q4}}
One equivalence(k=1) :
For group I ⇒ { q0, q3, q5}
δ:(q0, 0)→ q3 (nf)
δ:(q3, 0)→ q0 (nf)
⇒ (q0, q3)
δ:(q3, 0)→ q0 (nf)
δ:(q5, 0)→ q5 (nf)
⇒ (q3, q5)
δ:(q0, 1)→ q1 (f)
δ:(q3, 1)→ q4 (f)
⇒ (q0, q3) | q3=q0 ⇒ k=1
δ:(q3, 1)→ q4 (f)
δ:(q5, 1)→ q5 (nf)
⇒ q3≠q5 ⇒ k=1
for this q1≠q5
Now, P1 = {{ q0, q3}, {q5}}
For group II ⇒ { q1, q2, q4}
δ:(q1, 0)→ q2 (f)
δ:(q2, 0)→ q2 (f)
⇒ (q1, q2)
δ:(q2, 0)→ q2 (f)
δ:(q4, 0)→ q2 (f)
⇒ (q2, q4)
δ:(q1, 0)→ q2 (f)
δ:(q4, 0)→ q2 (f)
⇒ (q1, q4)
δ:(q1, 1)→ q5 (nf)
δ:(q2, 1)→ q5 (nf)
⇒ (q1, q2) | q1=q2 ⇒ k=1
δ:(q2, 1)→ q5 (nf)
δ:(q4, 1)→ q5 (nf)
⇒ (q2, q4) | q2=q4 ⇒ k=1
δ:(q1, 1)→ q5 (nf)
δ:(q4, 1)→ q5 (nf)
⇒ (q1, q4) | q1=q4 ⇒ k=1
Now, P1 = {q1,q2,q4}
P1 = {{q0, q3}, {q5}, {q1, q2, q4}}
Two equivalence(k=2) :
For group {q0,q3}
δ:(q0, 0)→ q3 (nf)
δ:(q3, 0)→ q0 (nf)
⇒ (q0, q3)
δ:(q0, 1)→ q1 (f)
δ:(q3, 1)→ q4 (f)
⇒ (q1, q2) | q1=q2 ⇒ k=2
For group {q1,q2,q4}
δ:(q1, 0)→ q2 (f)
δ:(q2, 0)→ q2 (f)
⇒ (q1, q2)
δ:(q2, 0)→ q2 (f)
δ:(q4, 0)→ q2 (f)
⇒ (q2, q4)
δ:(q1, 0)→ q2 (f)
δ:(q4, 0)→ q2 (f)
⇒ (q1, q4)
δ:(q1, 1)→ q5 (nf)
δ:(q2, 1)→ q5 (nf)
⇒ (q1, q2) | q1=q2 ⇒ k=2
δ:(q2, 1)→ q5 (nf)
δ:(q4, 1)→ q5 (nf)
⇒ (q2, q4) | q2=q4 ⇒ k=2
δ:(q1, 1)→ q5 (nf)
δ:(q4, 1)→ q5 (nf)
⇒ (q1, q4) | q1=q4 ⇒ k=2
P2 = {{q0, q3}, {q5}, {q1, q2, q4}}
Initial state which state contain q0 ⇒ {q0,q3}
q1,q4,q2 was the final states then final state ⇒ {q1,q2,q4}
q6 is non-reachable state remove it
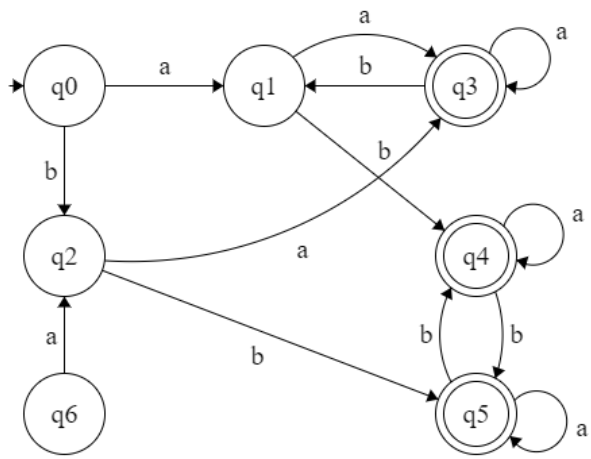
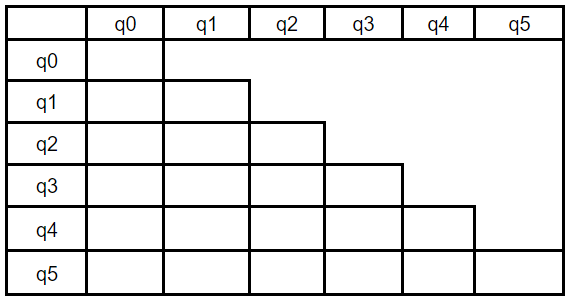
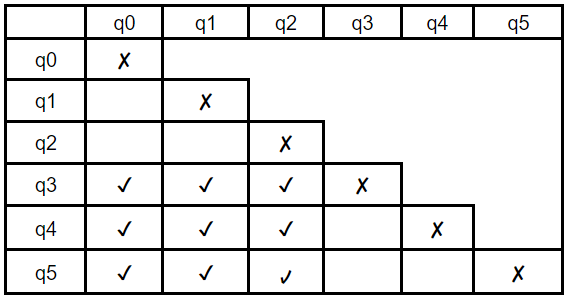
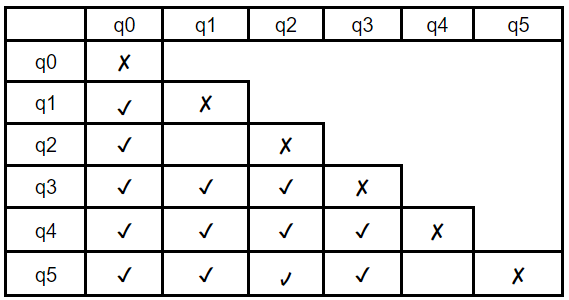
Step-1: Create the pairs of all the states involved in DFA
Step-2: Mark all the pairs (qi, qj) such a that qi is Non-Final state and qj is Final State.
Final State = {q3,q4,q5}
Non-Final state = {q0,q1,q2,q6}
Step-3: If there is any unmarked pair (qi, qj) such a that δ(qi,x) and δ(qj,x) is marked, then mark (qi,qj). x = { a, b }
q0,a→ q1
q1,a→q3
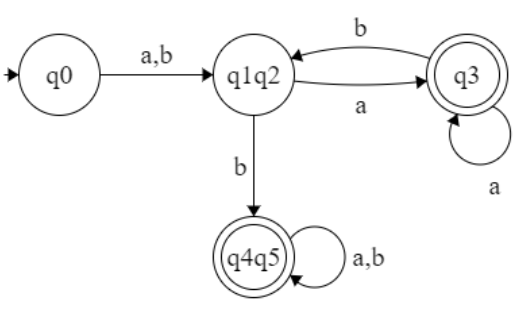
Step-4: Combine all the unmarked pairs and make them as a single state in the minimized DFA.
(q1, q2) and (q4,q5) are unmarked then q1=2 , q4=q5
/ima

.jpg)
.png)








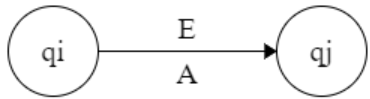
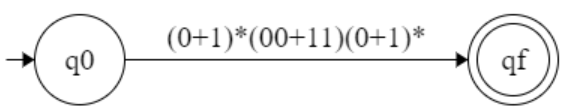
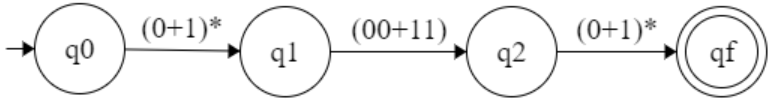
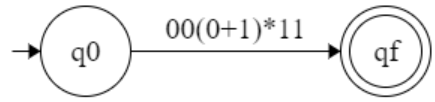
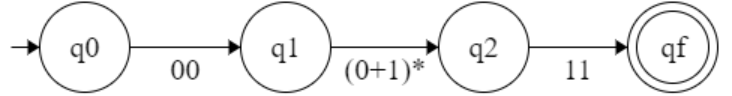
.png)