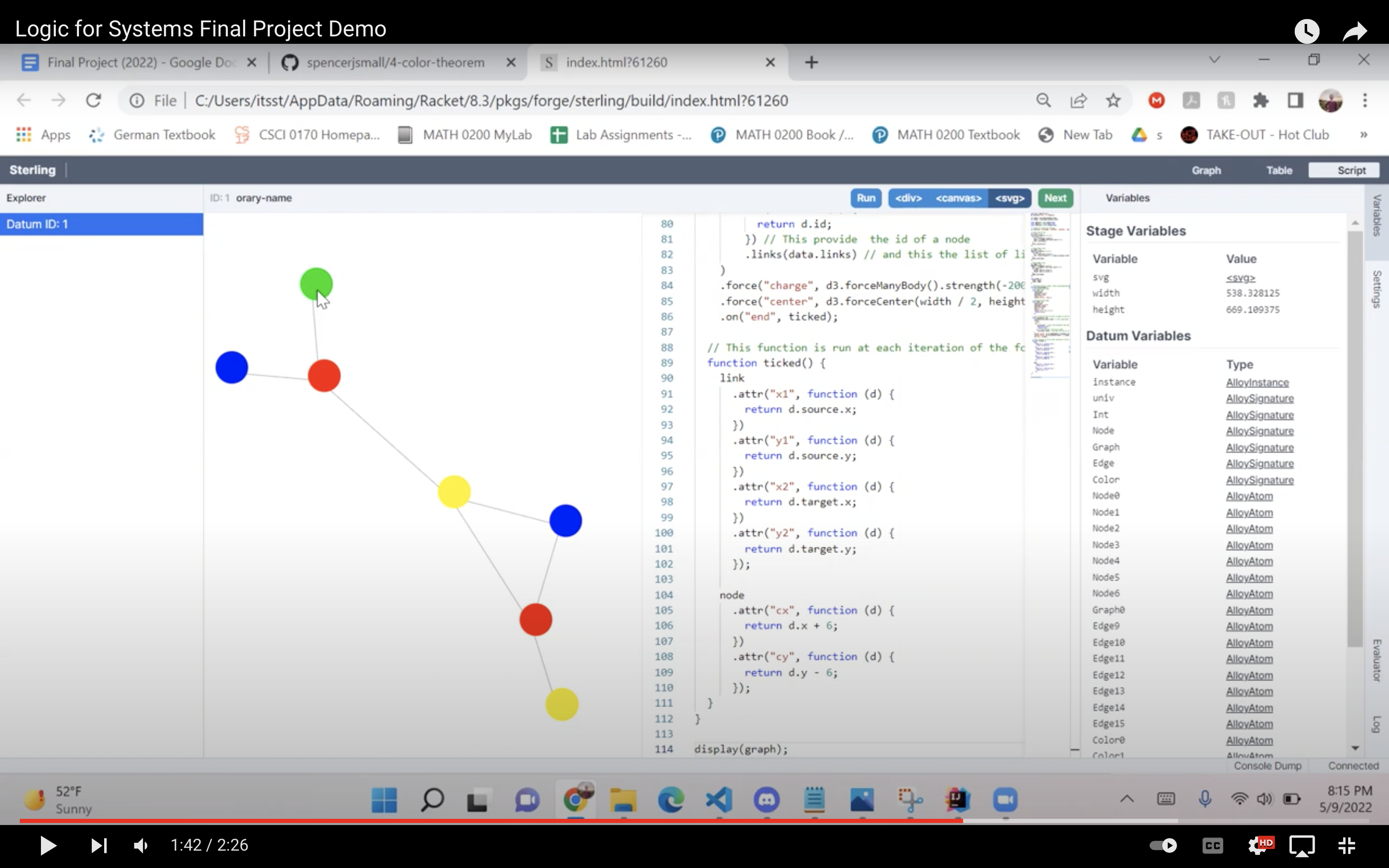
Our Forge model produces instances of connected, undirected graphs, containing sets of nodes and edges. The instances also contain node subsets of the graph, or Colors. We use these subsets to a) provide us with every combination of nodes (2n) in searching for K5 and K3,3 homeomorphic subgraphs, which would tell us the graph is nonplanar by Kuratowski's Theorem, and b) provide us with a schema to color the nodes of a planar graph in testing the Four Color Theorem. It must be noted that while the Four Color Theorem asserts the ability to color the regions of a planar graph using four colors such that no two adjacent regions share a color, we've abstracted this representation by coloring the nodes of a planar graph to represent the regions of an underlying planar graph:
In our abstracted representation, edges represent adjacency in the underlying graph. Thus, by proving that planarity implies a graph's nodes are four-colorable (as we do in test.frg), we are implicity proving that an underlying planar graph's regions are four-colorable.
At first, we struggled conceptually with how to structure our model. For instance, before we added an Edge sig we considered including connectivity as a field in the Node sig, but realized this would make searching for subgraphs impossible (i.e. a node should not be defined by its connections when wanting to consider subgraphs). We also played with having multiple Graphs in each instance, representing the parent graph and its subgraphs, but realized this would be too computationally expensive. Even our current implementation is quite expensive, given that it searches exhaustively for Kuratowski's subgraphs, so our is theorem verification of the Four Color Theorem is only possible for graphs of five nodes (although we can test discrete instances of larger graphs). Additionally, the only way we could figure out how to subdivide graphs (removing nodes and joining edges in looking for a homeomorphic subgraph – whose nodes are represented by a Color) allows for an edge to be joined in multiple ways. Thus, there are certain larger, complex nonplanar graphs that will pass our planarity tests.
Overall, we are happy with the performance of our model, even if it can only be used to verify the Four Color Theorem up to five nodes. We were warned that this project may be impossible to do in Forge alone, so we consider this a success. To view instances with the visualizer, simply adjust the run constraints at the end of model.frg before running racket model.frg from the command line (a nontrivial run statement for 9 Nodes and 16 Edges and has been provided as default). After Sterling has launched and rendered the data, you can then copy and paste the contents of viz.js into the blank SVG file under the Script tab. Our visualizer displays the planar graph instance and colors its nodes in such a way that satisfies the Four Color Theorem: