degree2

A SageMath package for computation of degree 2 Siegel modular forms

Installation

degree2 is a package written in pure Python. Place it an appropriate directory so that SageMath can find the package.

In the following, we illustrate how we install this package in "~~/sage_packages/". Of course the directory name may not be "~~/sage_packages/".

First install SageMath.
Open a terminal.

In SageMathCloud, one can open a terminal by creating a new file whose file type is "Terminal".

Create the directory and clone the repository.

mkdir ~/sage_packages
cd ~/sage_packages
git clone https://github.com/stakemori/degree2.git
cd degree2
git submodule init
git submodule update

Edit the init script file of SageMath to load the package.

touch ~/.sage/init.sage
cat ~/sage_packages/degree2/config/example_config.sage >> ~/.sage/init.sage

(Optional for vector valued Siegel modular forms) Set degree2.vector_valued_impl.utils.data_dir to an existing directory. And download cache data for vector valued Siegel modular forms. For example, we use '/home/your_user_name/degree2_data/vector_valued' for the data directory.
```
cd /home/your_user_name/degree2_data  # And download vector_valued.tar.gz to this directory.
tar xf vector_valued.tar.gz
```
Put the following lines to ~/.sage/init.sage.
```
import degree2.vector_valued_impl.utils
degree2.vector_valued_impl.utils.data_dir= '/home/your_user_name/degree2_data/vector_valued'
```

Basic Usage

Siegel-Eisenstein of degree two can be obtained by the function eisenstein_series_degree2. Siegel-Eisenstein series is normalized so that the constant term is one.
```
sage: es4 = eisenstein_series_degree2(4, 10)
sage: es4.prec
10
sage: es4[(2, 1, 3)]
2903040
```
The last line means that the Fourier coefficient of es4 at the half integral symmetric matrix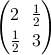 is 2903040. The third lines means that es4 knows Fourier coefficients of Siegel-Eisenstein series of weight 4 at half integral matrices whose maximum value of diagonal entries are less than or equal to 10.
Igusa's weight 10 , 12 and 35 cusp forms can be obtained by the function x10_with_prec, x12_with_prec and x35_with_prec respectively. These functions take one positive integer argument. The meaning of the argument is same as the attribute prec of es4, i.e. it means that the returned value knows the Fourier coefficients at half integral matrices whose maximum value of diagonal entries are less than or equal to the argument.
```
sage: x10 = x10_with_prec(10)
sage: x12 = x12_with_prec(10)
sage: x35 = x35_with_prec(10)
sage: x10[(1, 1, 1)]
1
sage: x12[(1, 1, 1)]
1
sage: x35[(2, -1, 3)]
1
sage: x35[(5, 1, 4)]
-759797709
```

One can add and multiply modular forms by + and *.

sage: es4 = eisenstein_series_degree2(4, 10)
sage: es8 = eisenstein_series_degree2(8, 10)
sage: es4 + es4
Siegel Modular form of weight 4 with prec = 10:
{(0, 0, 0) : 2,
 (0, 0, 1) : 480,
 (1, 0, 0) : 480,
 (1, 0, 1) : 60480,
 ...
 (10, 0, 0) : 544320}
sage: 2*es4 == es4 + es4
True
sage: es8 == es4 * es4
True
sage: es8 == es4^2
True

One can create the space of Klingen-Eisenstein series and cusp forms by the function KlingenEisensteinAndCuspForms.

sage: N47 = KlingenEisensteinAndCuspForms(47, 8)
sage: N47.dimension()
3
sage: N47.prec
8

Here N47 is the space of Klingen-Eisenstein series and cusp forms of weight 47, which is equal to the space of cusp forms of weight 47 because 47 is odd. Last line means each prec of the basis of N47 is 8.

One can compute the matrix of Hecke operator T(m) (m: a prime or a square of a prime) by the function N47.hecke_matrix.

sage: A = N47.hecke_matrix(2); A
[      -69045420294144   8646128852105428992 -33244506086178816000]
[              7688192       -53094861766656        17259429888000]
[            -16719872        26329615958016       -58220441763840]
sage: f = A.charpoly(); f
x^3 + 180360723824640*x^2 + 9700267079136838378586112000*x + 157899144590481648119705809591468032000000
sage: f.is_irreducible()
True
sage: K.<a> = NumberField(f); K
Number Field in a with defining polynomial x^3 + 180360723824640*x^2 + 9700267079136838378586112000*x + 157899144590481648119705809591468032000000

Here f is the characteristic polynomial of T(2) acting on N47 and K is the number field generated by a root a of f.

One can obtain an eigenform of weight 47 by the function N47.eigenform_with_eigenvalue_t2.

sage: x47 = N47.eigenform_with_eigenvalue_t2(a)

Here x47 is the weight 47 cusp form whose eigenvalue of T(2) is a.

sage: x47[(2, 1, 3)]
9031680*a + 526277673739804999680
sage: x47._construction
(-16719872*a - 685312149824691240960)*es4^3*x35 + (7688192*a + 159034476084886241280)*es6^2*x35 + (a^2 + 111315303530496*a + 2636772146839387523556311040)*x12*x35

The attribute _construction shows how x47 is constructed as a polynomial of Siegel-Eisenstein series of weight 4, 6 and cusp forms of weight 10, 12 and 35.

To construct the space of vector valued Siegel modular forms of weight det^* Sym(j), where j = 2, 4, 10, one can use the function vector_valued_siegel_modular_forms in the module degree2.vector_valued_smfs. This function uses structure theorems of weights det^* Sym(j) for j = 2, 4, 10. Structure theorems are known if j = 6, 8, but I have not implemented them yet.

The following code illustrate how one can construct a basis of the space of Siegel modular forms of weight det^13 Sym(10).

sage: from degree2.vector_valued_smfs import vector_valued_siegel_modular_forms as vvsmf
sage: M = vvsmf(10, 13, prec=6)
sage: M.dimension()
2
sage: M.basis()
[Vector valued modular form of weight det^13 Sym(10) with prec = diag_max 6,
 Vector valued modular form of weight det^13 Sym(10) with prec = diag_max 6]
sage: f = M.basis()[0]
sage: f[(2, 1, 3)]
(0, 1574304, 7610976, 33371712, 42535584, -3229632, 47605824, 112992768, -22784544, -10237632, -2096640)
sage: f[(2, 1, 3)][1]
1574304

One can construct Hecke eigenforms in a similar way to the scalar valued case.

sage: M.hecke_charpoly(2).factor()
(x - 84480) * (x + 52800)
sage: g = M.eigenform_with_eigenvalue_t2(84480)
sage: g.euler_factor_of_spinor_l(2).factor()
(1 - 133632*x + 8589934592*x^2) * (1 + 49152*x + 8589934592*x^2)

The function vector_valued_siegel_modular_forms uses Python's module multiprocessing. Sometimes it consumes much memory. To avoid multi-processing, use the following with statement.

sage: with degree2_number_of_procs(1):
....:    N = vvsmf(10, 20, prec=10)
....:    h = N.basis()[0]

License

Licensed under the [GPL Version 3][GPL] [GPL]: http://www.gnu.org/licenses/gpl.html