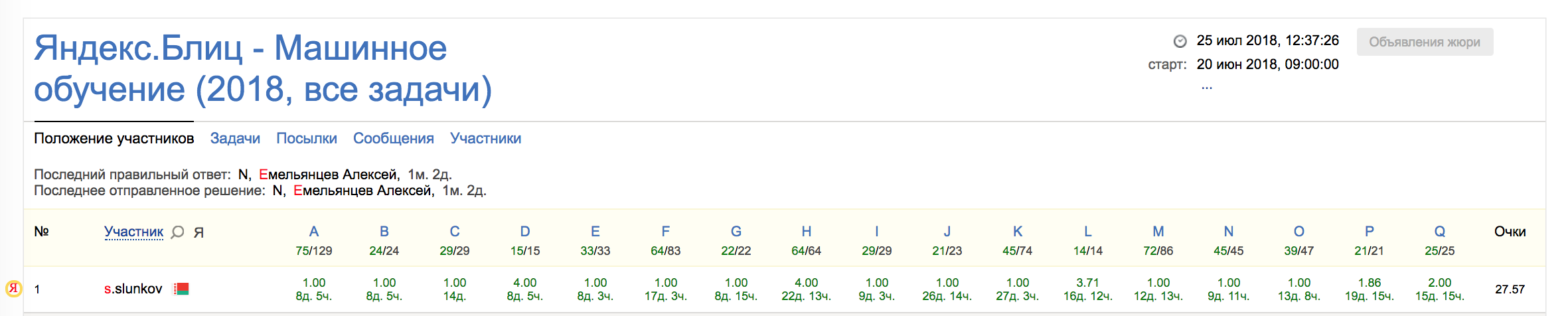
This repo contains solutions of all 17 tasks from all qualification and final rounds of Yandex.Blitz Machine Learning competition held in the end of June, 2018.
I didn't participate in the competition when it was really held so this is not real leaderboard (unfortunately). On the other hand I had more time to explore problems, learn something new and try different approaches.
Quickly jump to:
- A. Stump
- B. Coefficients restoration
- C. Freshness detector
- D. Feature selection
- E. Warm up
- F. Generalized AUC
- G. Permutations
- H. Restaurants
- I. Warm up
- J. Linear separability problem
- K. Unique queries
- L. Wi-Fi
- M. Pairwise ranking
- N. Coins
- O. SVD recommender
- P. Adversarial attack (white-box)
- Q. Adversarial attack (black-box)
The are 3 important observations here:
- All possible candidates for split (i.e. c value) are all points in the middle of 2 consecutive
$X$ coordinates (dashed lines in the image). So we have to check only$n-1$ variants (or less if some points have equal$X$ coordinates). - If we fix c then optimal values for a and b that minimize MSE would be just mean of
$Y$ coordinates of all points on each side of the split. - If we will naively calculate mean for each split by iterating over all points we'll get
$O(N^2)$ complexity which will not work, so instead we should sort all points by$X$ and then store sums of$Y$ and$Y^2$ for left and right sides of current split. Then going to next$X$ we can update those sums only by value of points that change side. Thus we will be able to easily compute mean as well as MSE for both sides and find split that minimizes MSE in$O(N)$ , though overall complexity will be$O(N \log N)$ due to sorting.
Implementation: a.py
Let's ignore noise and define the following function (MSE):
To find coefficients a, b and c we minimize this function using scipy.optimize.minimize.
Implementation: b.py
That is pretty straightforward classification problem. Though there are 2 question to address:
- How to use query text. Though we are provided with obfuscated query text, nevertheless we still can use standard
TfidfVectorizerfrom sklearn to calculate tfidf features - just need to customizetoken_patterna little bit. - How to perform validation. If we look at dates in train and test sets we'll notice that all dates in test data go the next day after training dates. Namely, training dates are 24-29 of January and test date is 30 of January. So in order to validate we can split training data into training - 24-28 of January and validation - 29 of January.
After we decided on these questions we can feed the data into a classifier. I used lightgbm for this purposes because it works well with sparse features and is very fast.
The last thing to note is that usage of query features is important for this task because without them we can only get
Implementation: c.ipynb
In order to extract most important features, we train catboost model with specified parameters CatBoostRegressor(n_estimators=200, learning_rate=0.1) and then use get_feature_importance method to extract top 50 most imporant features.
In the task statement it is said that cross-validation is being performed in inverse manner: we train on small amount of data (1000 samples) and validate on much larger data (9000 samples), so it is easy to overfit in this setting. The more features we have, the easier it is to overfit. Although we are constrained to select no more than 50 most important features, but we also could try to select less, and submit 40, 30, 20 top features. Indeed sending only 20 features gives us best result and we get 4 points (max for the task) on the leaderboard.
Implementation: d.ipynb
Just feed the data into sklearn LinearRegression model.
Implementation: e.ipynb
This problem looks less like machine learning problem but more like traditional competive programming problem.
Let's recall the formula for generalized AUC:
The naive solution would be to go over all pairs of
Let's try to put those points on a plane:
I ended up with several implementations for this task using C++ and Python and trying sorted array/binary tree. Though sorted array required
Implementation: f_naive.cpp, f_sorted_naive.cpp, f_fastest.cpp, f_sorted_naive.py
As it is said in the task description, stupid permutation function has a bug. As a result not all permutaitions occur evenly - some may occur more often while others less often. Let's generate 100000 stupid permutations and calculate how often each of numbers (0-7) was placed on each position (0-7).
Columns in matrix represent numbers, while rows - positions. Thus the number in each cell means how many times each number was on each position.
From the matrix we see, that the bug in stupid permutation causes some numbers to stay on initial position more often, than it should be if all permutations were evenly distributed. E.g. 0 stays on position 0, 1 on 1, 2 on 2 etc.
So all we are left to do is calculate number of such permutatations in groups of 1000 of them and sort by this number in ascending order, thus, random permutations will go first and stupid ones later.
Implementation: g.ipynb
We will use a simple linear model with 2 coefficients to predict restaurant score based on distance and rating:
We may notice that the expression we are asked to minimize is exactly the negative log likelihood (divided by constant N) or loss function of logistic regression:
Because logistic regression requires only labels 0 or 1 and target metric will be evaluated on pairs with known winner and looser, we will omit samples with ties (0.5 target) during training. To solve logistic regression we will use SGD.
After we obtain coefficients of scoring model we can use them to score all restaurants in the test data.
Another very important detail worth mentioning is rating and distance transformations before training. If we plot distance and ratings distributions we might notice that there are a lot of small distances near zero and ratings are concentrated around 7-8. Logically, users might be much more sensitive to difference between 100 meters and 1 km than 100km and 101 km. On the contrary low ratings 2 or 3 are percieved as almost equally poor, while difference between 8 and 9 rating feels more important. In order to take this into account, we might try to apply log transformation to distances and exponential transformation to ratings. Indeed, the model without any transformations scored 1.5 on the leaderboard, when using only distance transformation score raised up to 3.5, and after we applied both transformation we achieved max score of 4 points.
Implementation: h_exploration.ipynb, h.py
Although it is stated that we should find a linear function, I was unable to train linear model, so I used lightgbm, which might be an overkill for this task, but anyway.
As it is said that only few features are relevant, we'd like to find out what are those features.
We see that features 5 and 95 are the most important ones. Let's look at them and the target:
| 5 | 95 | 100(target) | |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 2 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 1 | 1 | 0 |
| 5 | 1 | 1 | 0 |
| 6 | 1 | 1 | 0 |
| 7 | 1 | 1 | 0 |
| 8 | 0 | 1 | 1 |
| 9 | 0 | 1 | 1 |
Looks like XOR:
Implementation: i.ipynb
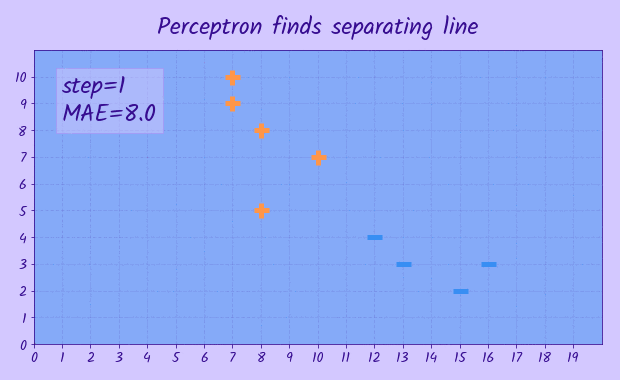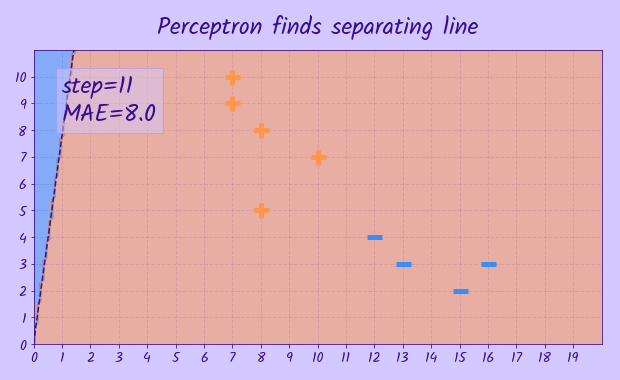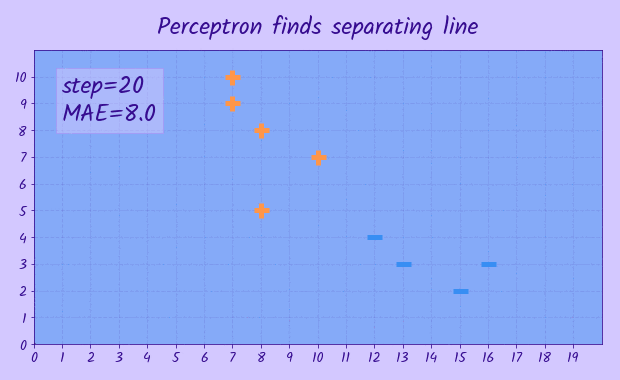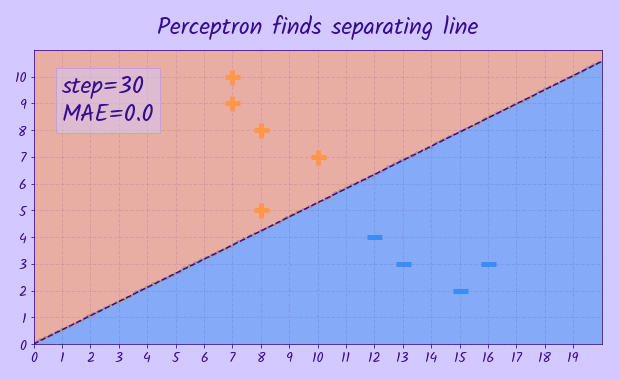
The task is given a set of points
Although there are a few linear models that might be applicable to this task, namely linear/logistic regression, SVM, perceptron, not all of them will find a hyperplane that splits all points exactly. This can happen if, according to the respective loss function, it is 'cheaper' to misclassify a single point, but the total loss for other points will be less. Though it doesn't apply to the perceptron model - it tries to find separating hyperplane, that splits the classes exactly, if it is possible, but if not it will never converge. In the task statement it is said that the input dataset is known to be linearly separable, so we can use the perceptron here. During training only points that are misclassified contribute to the error, so if a point was already classified correctly it doesn't matter how far it is from decision boundary, so we may end up with decision boundary being very close to some of training points, but in our task that is acceptable, as we don't have any other requrements for the hyperplane.
The perceptron model has
In order to find the parameters of vector
Despite linear/logistic regression might not always find separating hyperplane correctly, my solutions using both of them were accepted - probably the tests were not so hard and the points were separated by a wide margin.
Implementation: j.py
The idea for this task is to implement some kind of Bloom filter. Some kind because actually we will use k = 1 (number of filters). So it will be more like regular hash-table but without storing the values of elements - only their hashes. There is a formula for calculating false positive rate of Bloom Filter depending on number of unique elements, size of filter and number of filters, but for me it was easier to write a small test to check the error rate for various combinations of parameters.
I used 2 a bit different implementations, though in both of them I used bytearray which I never used before - that is just, as its name says, array of bytes, just more memory efficient than usual list of any objects. Using it, it was possible to allocate array of 1,000,000 elements keeping memory usage below 5MB. That is more bytes that we could probably allocate if we were using C++, because its memory limit was 10x times lower - just 500KB. For calculating hashes of queries I used built-in function hash which is actually used for hashing elements in regular python hash-tables aka dicts.
So, being able to use hash-table of size 1,000,000 it was possible to implement a very straightforward solution, using whole bytes to store just 1 bit of information - whether we've seen such hash before or not. Though, probably the error rate was pretty close to 5%. Another a bit more sophisticated but more robust approach was to use every bit of a single byte, thus we can achieve even lower error rates using just 200,000 bytes.
Implementation: k_test.ipynb, k_bytearray.py, k_bitarray.py
The most important observation in this task is similarity between ssid and organization name for those rows where target=1. Here are just a few samples with target=1:
| id | names | ssid |
|---|---|---|
| 18 | ["Аэропорт Толмачево, бухгалтерия", "Толмачево"] | Tolmachevo-MTS-Free |
| 38 | ["Kontrolmatik"] | Kontrolmatik_Staff |
| 49 | ["ПКВ Моторс", "Pkw Motors", "Pkw Motors", "Те... | PKW Guests |
| 77 | ["Техцентр Юста", "Tekhtsentr Yusta", "Юста", ... | YUSTA |
| 94 | ["Респект Авто", "Автосервис"] | RespectAuto |
While ssid contains mostly latin characters, organization names might be in other languages like russian, so we need to perform some transliteration before calculating similarity. After that we will compute similarity between 2 strings as number of n-grams ocurred in both strings. We will use n=1..8. Also we'll compute similarity for ssid and urls fields, because urls might also include some substrings from ssid.
Other features are more obvious: we calculate distance between user and organization and perform one-hot encoding of rubrics. Also we feed some fields as is, like has_wifi, publishing_status.
For validation I used 20% of data. Though it was important to perform group-aware splits, that's why I used GroupShuffleSplit which places all samples from one group to either train or test set, so that test and train sets have non-intersecting groups.
For training I used lightgbm model, which after 170 iterations scored 3.71 on the leaderboard that corresponds to 95% accuracy.
Implementation: l.ipynb
This task might look similar to H. Restaurants. The training dataset here is also composed of pairs of items and we are asked to maximize log likelihood of the data. Though, unlike task H, here we don't have any features of objects that can be used as input to scoring model, so instead we will consider each
Thus our task can rewritten as:
Or in vectorized form:
Where
There is always
After those preparations we can just fit logistic regression to obtain scores
Implementation: m.py
Well, the first straightforward idea was simply to calculate frequency of getting heads up
Unfortunately my understanding of Bayessian statistics not as profound as I'd like, but the idea is that instead of estimating a single number
That was an overall justification, now let's get to our task. According to wikipedia articles Checking whether a coin is fair and Beta distribution we know that the a posterior distribution of
From the properties of
Implementation: n.py
This task is classical recommender system. It is well known since Netflix competition in 2006-2009. One of the competitors Simon Funk has really nice description of his method that uses SGD to find matrix factorization. It is good, because we don't need to deal with huge sparse matrices.
Another useful resource was suprise library. It does exactly what is required in our task and it has convenient methods to get sample data for testing purposes. We will try to implement our own algorithm to find matrix factorization and compare the results with those received using this library.
The algorithm is pretty straightforward. The idea is to represent ratings as
Where:
We initialize these variables with some random values and then iterate over each known user-movie-raiting tuples and compute error. Then we update just a little bit all parameters to minimize the error:
Where
Implementation: o_test.ipynb, o.py
The idea is to start with the source image and incrementally update it a little bit in opposite gradient (w.r.t. input image) direction, so that with each iteration the model predicts higher and higher probability that the image belongs to the target class. As long as we know the underlying model is plain linear classifier with softmax activation, we can analytically compute the gradient of the loss function w.r.t. the input.
The loss function that we are going to minimize is:
Where
The whole gradient in vector form can be written as:
Where
Then incremental update rule will be:
Implementation: p.ipynb
This task is similar to the previous white box adversarial attack, but here we don't have direct access to gradient, so we need to somehow estimate it using only output of the classifier.
There are a few different approaches to do it:
- Use substitute network - new model that is trained to give the same answers as black-box model. And then hope that it's gradients are similar to the gradients of original model.
- Use finite difference method to estimate gradient, while being precise it requires as much model evaluations as the dimensions of input image. We have 32x32x3 input image, so there will be 3072 evaluations per iteration. It actually may be acceptable but we'll use another method.
-
Natural Evolution Strategies (NES). This method is well described in the Black-box Adversarial Attacks with Limited Queries and Information paper. In short we choose
$n$ points in the neighborhood of$x$ and estimate gradient using function values at those points using formula:
Where
Here we don't depend on size of the input image and we can choose
After roughly 5000 iterations we've got desired target class probability > 0.5. It look like the MSE=687 is quite large (much larger than 235 which is the threshold to get max points for this task) and the image is distorted quite a lot. After spending some time figuring out what's wrong and how it is possible to approach much lower threshold, I submitted this solution and got good results. As it turned out there was only one test for this task and the input image in it required less distortions to fool the classifier, so it worked well. After tuning learning rate, regularization parameter and number of points for NES the desired threshold was reached.
Implementation: q_visualization.ipynb, q.py