pyodesys provides a straightforward way of numerically integrating systems of ordinary differential equations. It unifies the interface of several libraries. It also provides a convenience class for representing and integrating ODE systems defined by SymPy expressions.
The numerical integration is perfomed using eiher:
Note that implicit steppers which require a user supplied callback for calculating the jacobian is provided automatically by pyodesys.
Autogenerated API documentation is found here: http://hera.physchem.kth.se/~pyodesys/branches/master/html
Simplest way to install pyodesys and its (optional) dependencies is to use the conda package manager:
$ conda install -c bjodah pyodesys pytest $ python -m pytest --pyargs pyodesys
Optional requirements not listed in requirements.txt:
- pygslodeiv2 (>=v0.5.0)
- pyodeint (>=v0.6.0)
- pycvodes (>=v0.3.0)
Source distribution is available here: https://pypi.python.org/pypi/pyodesys
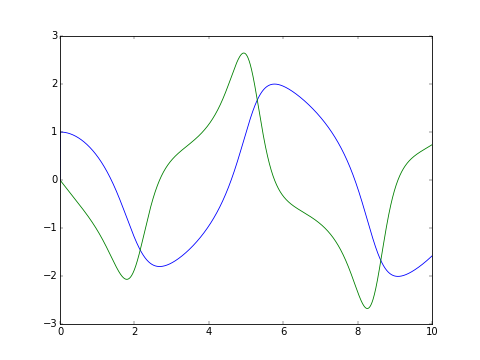
The classic van der Pol oscillator (see examples/van_der_pol.py)
>>> from pyodesys.symbolic import SymbolicSys
>>> def f(t, y, p):
... return [y[1], -y[0] + p[0]*y[1]*(1 - y[0]**2)]
...
>>> odesys = SymbolicSys.from_callback(f, 2, 1)
>>> xout, yout, info = odesys.integrate(10, [1, 0], [1], integrator='odeint')
>>> _ = odesys.plot_result()
>>> import matplotlib.pyplot as plt; plt.show() # doctest: +SKIPfor more examples, see examples/, and rendered jupyter notebooks here: http://hera.physchem.kth.se/~pyodesys/branches/master/examples
The source code is Open Source and is released under the simplified 2-clause BSD license. See LICENSE for further details. Contributors are welcome to suggest improvements at https://github.com/bjodah/pyodesys
Björn I. Dahlgren, contact:
- gmail address: bjodah
- kth.se address: bda