适用于单表盘、单指针仪表刻度的计算。
(1)模板匹配:为了分割仪表盘,使用了OpenCV的模板匹配模块,这里使用了两次匹配从粗到细。
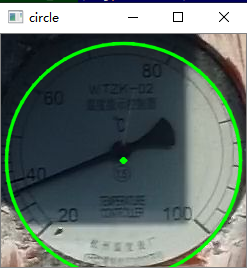
(2)获取表盘圆心,半径:使用了霍夫圆检测算法
(3)二值化:Kmeans算法
(4)获取指针相对横轴的角度:直线拟合
(5)鼠标获取0刻度坐标
(6)角度计算:计算0刻度与指针向量的角度(不是实际刻度)
(7)实际刻度还没做。
首先说一下模板匹配,它是OpenCV自带的一个算法,可以根据一个模板图到目标图上去寻找对应位置,如果模板找的比较好那么效果显著,这里说一下寻找模板的技巧,模板一定要标准、精准且特征明显。 第一次的模板选取如下:
def get_match_rect(template,img,method):
res = cv2.matchTemplate(img, template, method)
匹配的效果如下:
根据模板选取的原则我们,必须进行两次匹配才能的到精确和更高准确率的结果 第二次的模板如下:
然后在第一次结果的的基础上也就是蓝色矩形框区域进行第二次匹配,结果如下:
def detect_circles(self,gray,img):
# 需要调整参数,获取圆
circles=cv2.HoughCircles(gray, cv2.HOUGH_GRADIENT, 1, 80, param2=20, minRadius=5)
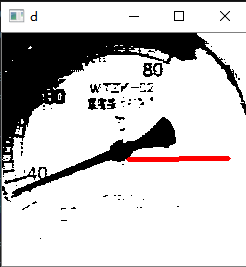
下面对上图进行k-means二值化,由于途中的阴影,所以只截取原图的0.6(从中心)作为k-means聚类的样本点,然后将聚类结果应用至上图并重新二值化(聚类结果为2,求中值,根据中值二值化),同时只保留内切圆部分,效果如下:
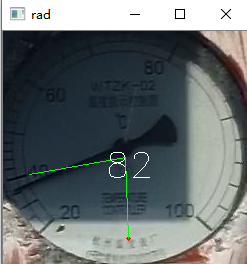
接下来就是拟合直线,拟合直线我采用旋转虚拟直线法,假设一条直线从右边0度位置顺时针绕中心旋转当它转到指针指向的位置时重合的最多,此时记录下角度,最后根据角度计算刻度值。 效果图如下:
最后就读取到了数值:
聚类结果:
[[31.99054054 23.04324324 14.89054054]
[62.69068323 53.56024845 40.05652174]]
重合数量和对应坐标: (1566, (26.73 143.50))
点击0刻度位置
markzero(new_)
angle((c_x, c_y, opint[0], opint[1]), (c_x, c_y, x, y))