/rust-crdt

a collection of well-tested, serializable CRDTs for Rust

Primary LanguageRustApache License 2.0Apache-2.0

Build Status crates.io docs.rs

crdts: family of thoroughly tested hybrid crdt's.

A family of CRDT's supporting both State and Op based replication.

what is a CRDT?

CRDT's are the solution to highly available mutable state.

CRDT expands to Conflict Free Replicated Data Type, it refers to a family of structures that know how to merge without conflicts. There are two main sub-families of CRDT's: CvRDT and CmRDT. They differ in how they replicate. CvRDT's are state based, meaning you would ship the entire CRDT state across the network to your peers. CmRDT's instead replicate by distributing all edits (called Op's) to each node in your system.

Here we'll take a quick look at CRDT's, for the sake of clarity and brevity, we'll focusing only on CvRDT (all ideas still apply to CmRDT's). CvRDT structures define a merge(a, b) operation which takes states a and b produces a merged state. A simple example is the GSet (grow-only set), it's merge is the union of the two sets.

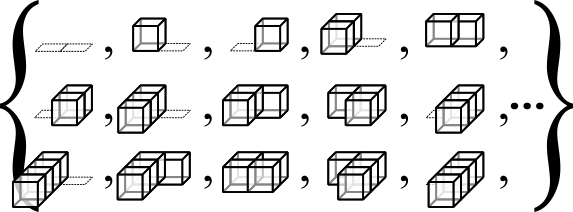
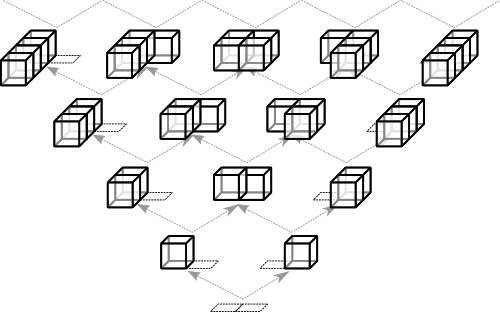
an attempt to understanding CRDT's by building one

CRDT's are all about partial orders, to turn a structure into a CRDT, you must first define a special kind of partial order over the state space of your structure. You must do this carefully as the partial order also defines how your merge behaves. For example lets take a look at the state space of a 2-tuple like structure that stores cubes in two slots, it's state space looks like so:

To make this structure a CRDT, we need a partial order over the state space that satisfies the folowing constraint:

∀ s ⊆ S where S is your state space  # for any subset of the state space ...
∃ lub s and lub s ∈ S                # .. the least-upper-bound of the set is also in the state space

lub is the Least Upper Bound operation, it takes a subset of the state space and produces a unique state that is greater than or equal to all states in the subset. Here's a partial order that satisfies the constraints:

Now say we want to merge two instances of this structure, well turns out we've already done the hard part as the partial order tells us what the final merged state will be.

merge(a, b) = lub { a, b }

The merge(a, b) operation is exactly the same as computing the least-upper-bound of the set {a, b}.

Looking over this partial order, we can derive a few other properties of CRDT's.

  1. merge(a, b) always causes us to go up or stay the same
  2. By 1. merge's are idempotent, since a previous state will be below or equal to the current state, remerging stale states will have no effect.
  3. merge(a, b) is reflexive, commutative and associative

How to use this library

Interacting with the CRDT's

Working with a CRDT is a bit different from datastructures you may be used to. Since we may be acting on data that is concurrently being edited by others, we need to make sure that your local edits only effect the data that you've seen.

Bad way of interacting with CRDT's

For example, if you clear a Map, we want to be able to say that this clear operation will only effect entries in the map that you are aware of. If you are not tracking this causal history of your edits correctly, you could end up deleting data that you are not aware of. e.g. a good way to lose data would be to do something like this:

  1. you receive a Map CRDT from across the network.
  2. you read the Map's key/value pairs and display them to the user.
  3. you receive an updated version of the Map CRDT but the user has not refreshed their view.
  4. The user chooses to clear the values of the Map. So you call Map::clear() on your CRDT.

At this point you've potentially cleared data that the user didn't want to clear. To fix this, we need to include a Causal context with the clear operation. This causal context is a vector clock (VClock) that stores the version of the Map that was seen by this user when they decided to Map::clear().

Good way to interact with CRDT's

Lets take a look at what interacting with CRDT's looks like when using crdts.

  1. First create an instance of the CRDT, we'll use the MVReg (Multi-Value Register) CRDT for this example. It allows us to store a value and resolves concurrently set values by keeping both values.
let mut reg = MVReg::new();
  1. To set a value in your CRDT, you'll need to provide a context (even for the initial value), the only way to get a context is to first read from the CRDT.
let read_ctx = reg.read();
assert_eq!(read_ctx.val, vec![]); // the registers is empty!
  1. Reading any state from a CRDT will produces a ReadCtx.to access the value from the ReadCtx, use the .val field. From the example above we see the register is currently not storing any values (empty Vec).

Now to make your edit to the reg, you'll derive the appropriate context for the edit you want to make, for edits that remove data, you'll need to use .derive_rm_ctx(), for adding new data you'll need .derive_add_ctx(<actor_id>) where <actor_id> is a unique identifier of whatever is acting on the CRDT.

let add_ctx = read_ctx.derive_add_ctx(123);
let rm_ctx = read_ctx.derive_rm_ctx();

reg.set("Value".to_string(), add_ctx);                // We set the value of the register using the Add context
reg.clear(rm_ctx);                                    // We remove using the (stale) Rm context
assert_eq!(reg.read().val, vec!["Value".to_string()]) // and we see that the MVReg::clear() did not remove the new value

Now you may be wondering why we have a "Value" after we've cleared the register. The "Value" string was added with an AddContext that included a marker showing that new information from actor 123 was present. The clear operation used an RmCtx that was derived from a read where we did not have this information from actor 123, only data that was seen at the time of the read that the RmCtx was derived from is removed.

Another trap you may fall into is reusing a context derived from one part of the CRDT to edit another part of the CRDT. Steps to lose data:

let read_ctx = map.get(&"key 1".to_string());
map.rm(&"key 2".to_string(), read_ctx.derive_rm_ctx());

Now you're using an RmCtx derived from another key, this RmCtx should only be used to remove the same data that it read. Same goes for the AddCtx, it should only be used to overwrite data that it had been derived from.

If you keep these things in mind, you'll have a good time :)

Further reading

If you want to learn about how CRDTs work, I suggest starting with the readme from aphyr's meangirls repo. Afterwards, either check out the riak dt source code or A comprehensive study of CRDTs depending on if you like to read papers or jump straight to source code examples.

references