A PyTorch implementation of Neighbourhood Components Analysis by J. Goldberger, G. Hinton, S. Roweis, R. Salakhutdinov. NCA is a metric learning technique that learns a linear transformation of the dataset such that the expected leave-one-out performance of kNN in the transformed space is maximized.
For a more detailed explanation of NCA, check out the accompanying blog post.
You can install torchnca with pip:
pip install torchnca
from torchnca import NCA
# instantiate torchnca object and initialize with
# an identity matrix
nca = NCA(dim=2, init="identity")
# fit an torchnca model to a dataset
# normalize the input data before
# running the optimization
nca.train(X, y, batch_size=64, normalize=True)
# apply the learned linear map to the data
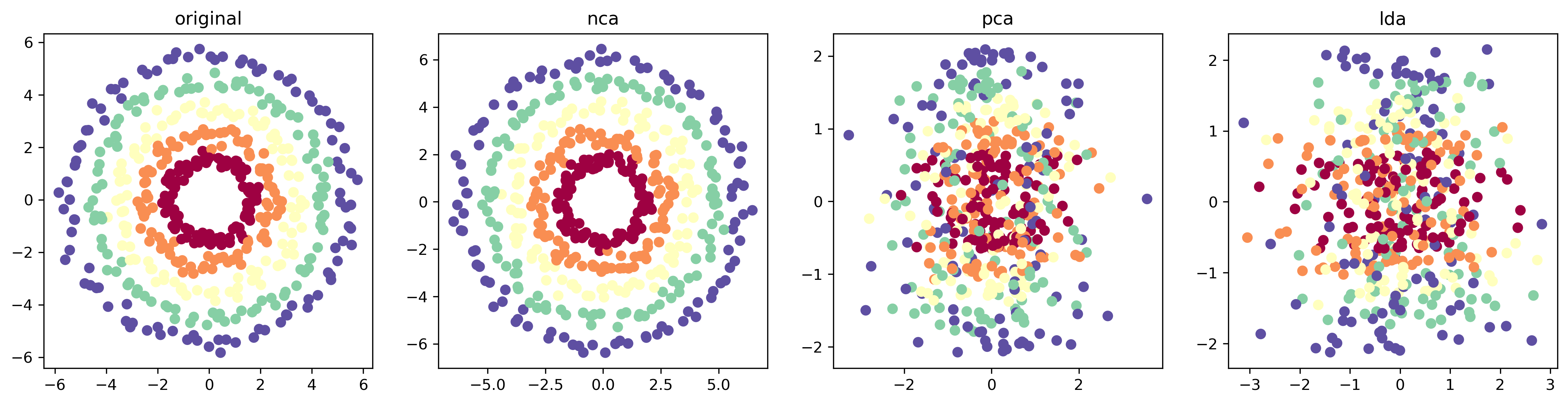
X_nca = nca(X)We generate a 3-D dataset where the first 2 dimensions are concentric rings and the third dimension is Gaussian noise. We plot the result of PCA, LDA and NCA with 2 components.
Notice how PCA has failed to project out the noise, a result of a high noise variance in the third dimension. LDA also struggles to recover the concentric pattern since the classes themselves are not linearly separable.
We compute the classification error, computation time and storage cost of two algorithms:
- kNN (k = 5) on the raw 784 dimensional MNIST dataset
- kNN (k = 5) on a learned 32 dimensional NCA projection of the MNIST dataset
| Method | NCA + kNN | Raw kNN |
|---|---|---|
| Time | 2.37s | 155.25s |
| Storage | 6.40 Mb | 156.8 Mb |
| Error | 3.3% | 2.8% |