python-dsa: A Python repository from symonk

python-dsa

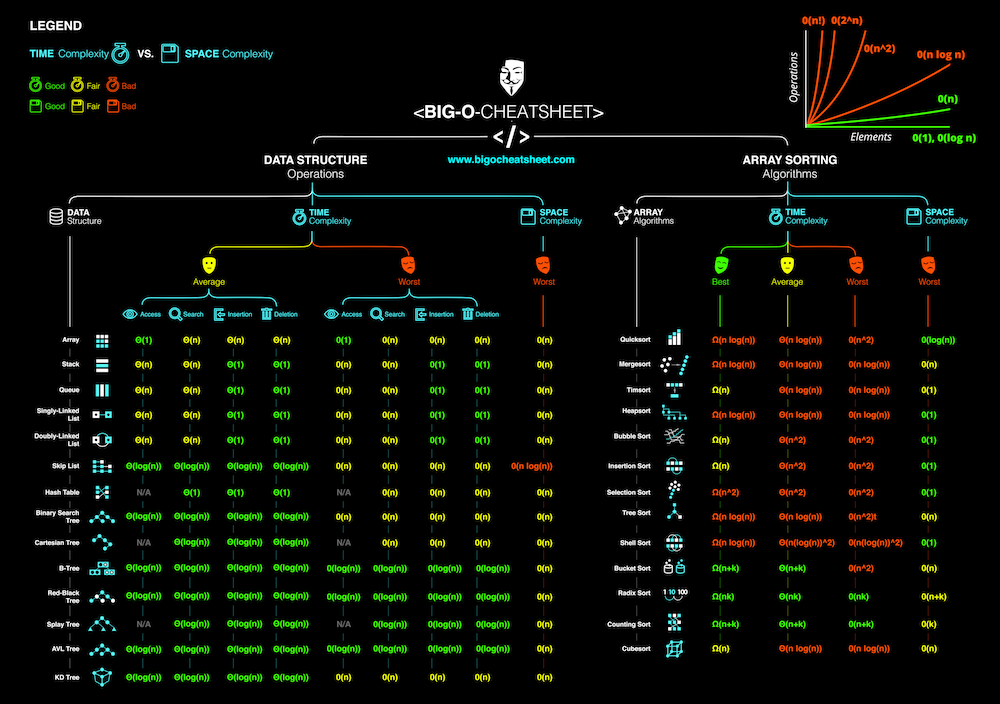
🐍 Data structures and Algorithms in python

Constant Complexity [O(1)]

Where the algorithm time remains the same, regardless of the input size growing.

# O(1) constant time
x = [1,2,3]
assert x[0] == 1

Linear Complexity [O(n)]

Linear complexity is when the time/space of the algorithm grows in line with the size of the input, for example: A bigger array takes longer than a smaller one to traverse.

numbers = list(range(10_000))
for n in numbers:
    # We have to iterate every element in numbers; O(n) depending on numbers size.
    _ = n * 2

Logarithmic Time [O(log n)]

Logarithmic time/space complexity typically halves the input on each iteration. A good example is finding the phone number of someone in a phone book, the optimal solution would be to keep cutting the book in half, throwing the half away that the name does not exist in. Typically solutions that can work in O(log n) time are sorted already.

def search_phone_book(book: list[string], name: string) -> int:
    """Find a person in a phone book, return their index.
    Returns -1 if the person does not exist."""

    left, right = 0, len(phone_book)-1
    while left <= right:
        middle = (left + right) // 2
        choice = book[middle]
        if choice == name:
            return middle
        # rely on default string sorting.
        if choice < name:
            left = middle + 1
        else:
            right = middle -1
    return -1


phone_book = ["Alistar", "Bert", "Christopher", "Diane", "Ezmerelda"]
assert search_phone_book(phone_book, "Diane") == 3
assert search_phone_book(phone_book, "Robert") == -1

The above algorithm is known as divide and conquer and is extremely performant as data sizes scale.

Polynomial Time [O(n²)]

Polynomial time typically involves iterating through an input multiple times, depending on how many nested iterations, describes the exponent.

input = (1,2,3,4,5,6)
for n in input:
    print("O(n)")
    for i in input:
            print("O(n²)")
        for j in input:
                print("O(n³)")
            for y in input:
                print("O(n⁴)")

Exponential Time [O(n^²)]

In an exponential algorithm, the runtime of the algorithm often doubles (or more) for a single increase in the input data. This is usually common in brute force style algorithms.

# Note: This can be sped up substancially by caching calls.
def fibonacci(n: int):
    if n <= 1:
        return n
    return fibonacci(n-1) + fibonacci(n-2)

A boost im performance can be had here via:

from functools import lru_cache

@lru_cache
def fibonacci(n: int):
    if n <= 1:
        return n
    return fibonacci(n-1) + fibonacci(n-2)