Háromszögeléssel történő helyzetmeghatározás pontossághígulási (DOP) értékei

Bevezető gondolatok

Ez a repozitórium a ‘Ferenci Tamás - A háromszögelés precíz hibaanalízisének néhány lehetősége’ videóban vizsgált egyik kérdés, a háromszögelés pontossághígulásának (DOP) kiszámításához tartozó programkódokat mutatja.

A programkód

Segédfüggvények

A vizualizáláshoz a ggplot2 csomagot fogjuk használni:

library(ggplot2)

Jól fog jönni a Moore-Penrose pszeudoinverz:

pinv <- function(x) solve(t(x)%*%x)%*%t(x)

Defináljunk egy függvényt, ami megadja adott oldalú szabályos sokszög csúcsainak koordinátáit (az ilyen elrendezésű adótornyok esetének vizsgálatához):

PolygonPoints <- function(n, a = 1) data.frame(x = a*cos(2*pi*((1:n)-1)/n), y = a*sin(2*pi*((1:n)-1)/n))

DOP számítás

A videóban részletesen bemutatott FOSM (elsőrendű, második momentumig menő) közelítés implementációja:

DOPFOSM <- function(vehicle, stations) {
  H <- t(sapply(1:nrow(stations), function(j)
    c(-(vehicle$y-stations$y[j]), vehicle$x-stations$x[j])/
      ((vehicle$x-stations$x[j])^2+(vehicle$y-stations$y[j])^2)))
  G <- t(H)%*%H
  if(rcond(G)<.Machine$double.eps) NA else sqrt(sum(diag(solve(G))))
}

A paraméterek az adók pozíciói (stations) és az, hogy melyik pontban kérdezzük le a DOP-ot (hol van az egység ami a helymeghatározást végzi, vehicle).

A videóban utalásszerűen szerepelt MC (Monte Carlo-szimulációs) módszer implementációja:

DOPMC <- function(vehicle, stations, Nsim = 10000, noisesd = 0.1) {
  mcres <- t(replicate(Nsim, {
    thetas <- sapply(1:nrow(stations),
                     function(i) atan((vehicle$y-stations$y[i])/(vehicle$x-stations$x[i])))
    thetasnoise <- thetas + rnorm(nrow(stations), 0, noisesd)
    as.vector(pinv(cbind(tan(thetasnoise), -1)) %*% (tan(thetasnoise)*stations$x - stations$y))
  }))
  sqrt(var(mcres[,1]) + var(mcres[,2]))/noisesd
}

Az előbbieken túl további paraméter a szimulációk száma (Nsim) és a rákevert – normálisnak feltételezett – zaj szórása (noisesd).

Egy teljes rács végigszámításához definiáljunk egy külön függvényt:

DOPgrid <- function(simgrid, stations, method = DOPFOSM) {
  sapply(1:nrow(simgrid), function(i) method(simgrid[i,], stations))
}

simgrid <- expand.grid(x = seq(-2, 2, 0.01), y = seq(-2, 2, 0.01))

Eredmények

E függvények használatával már könnyen kiszámíthatjuk a DOP-okat különböző geometriákra.

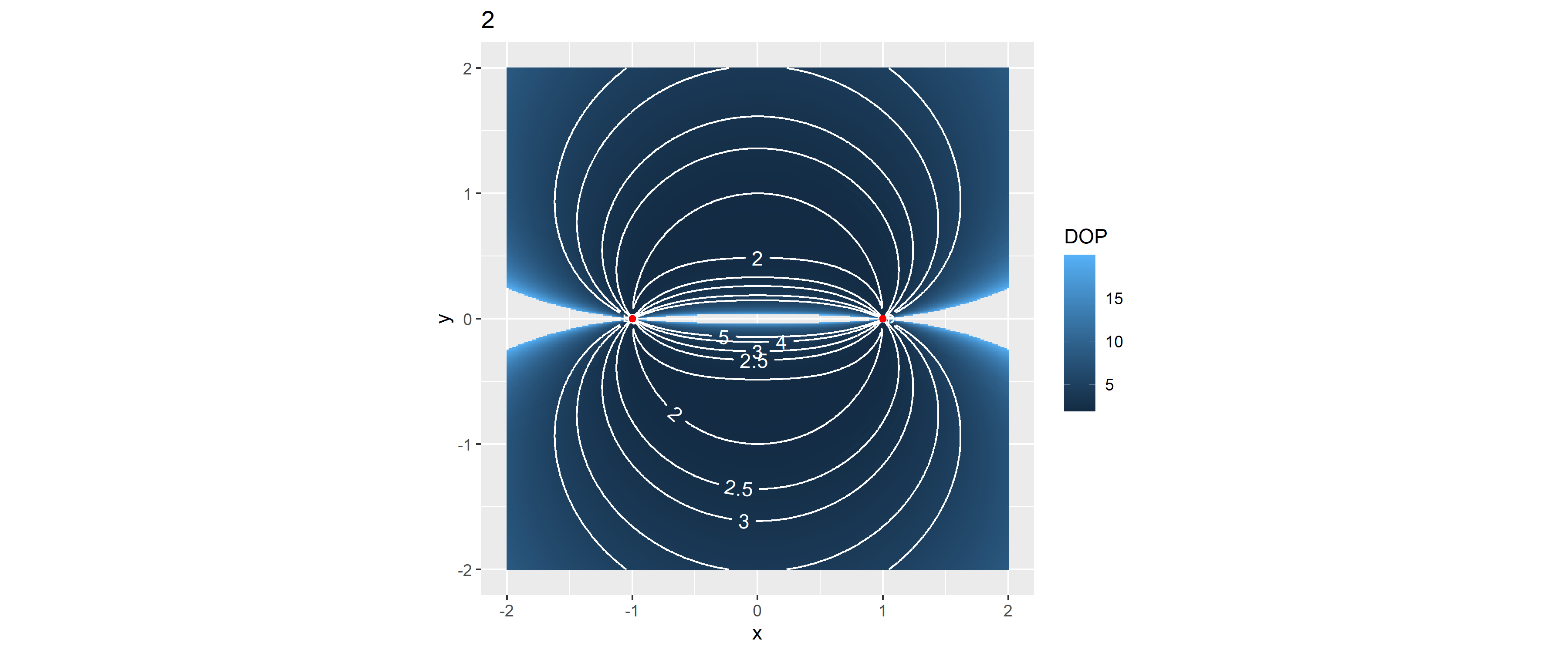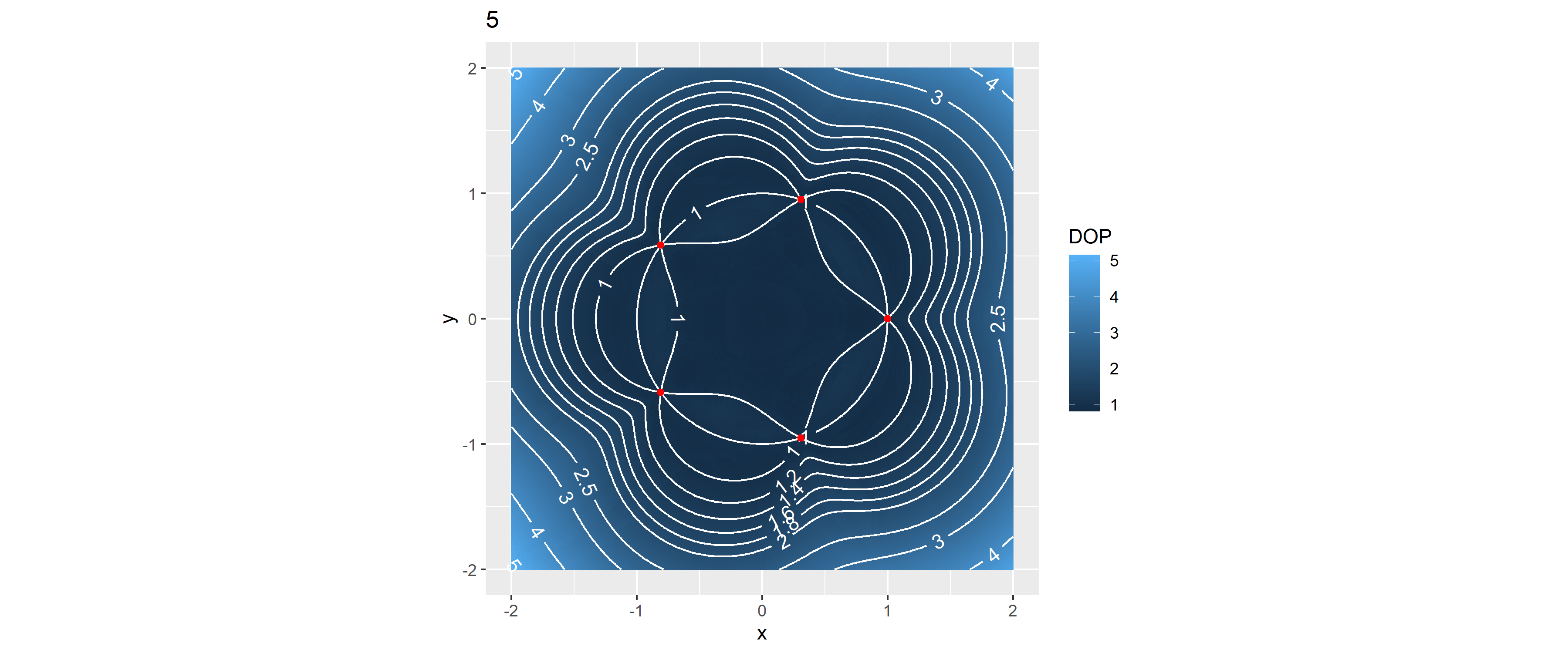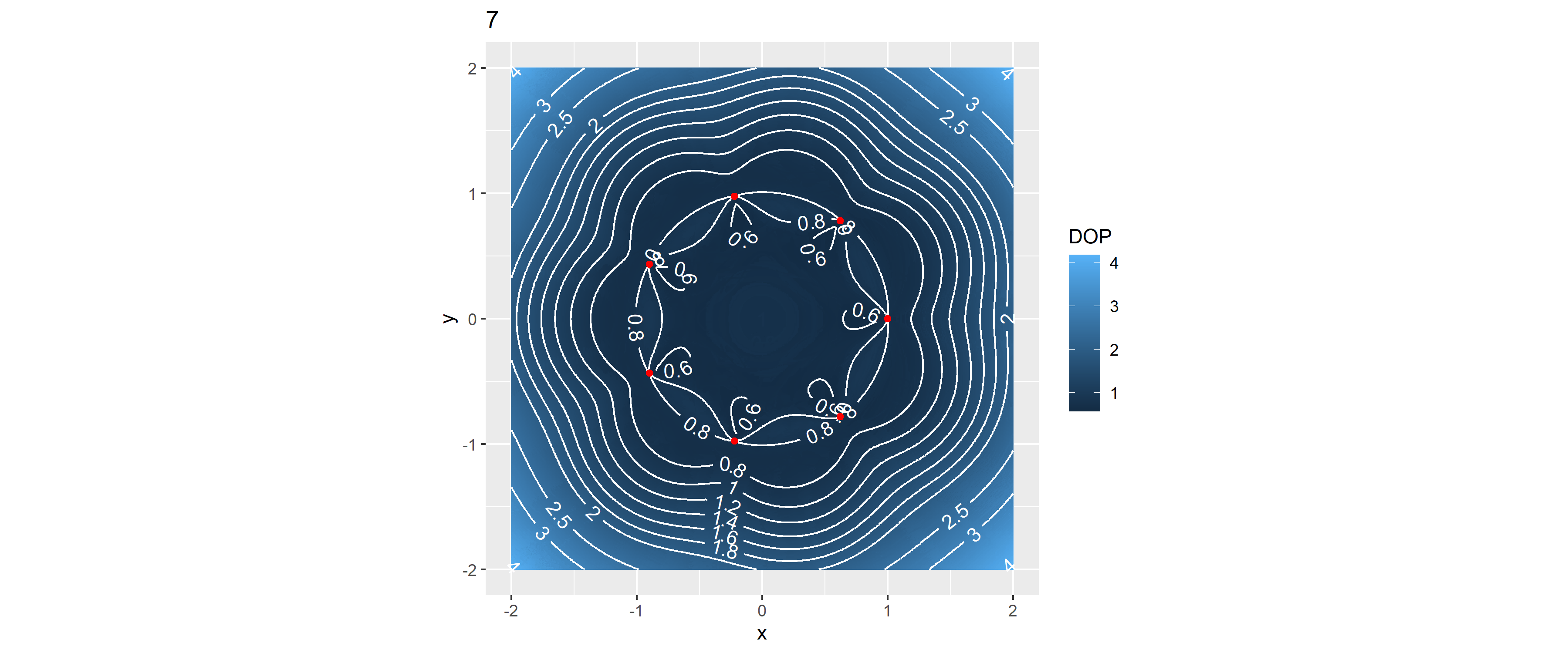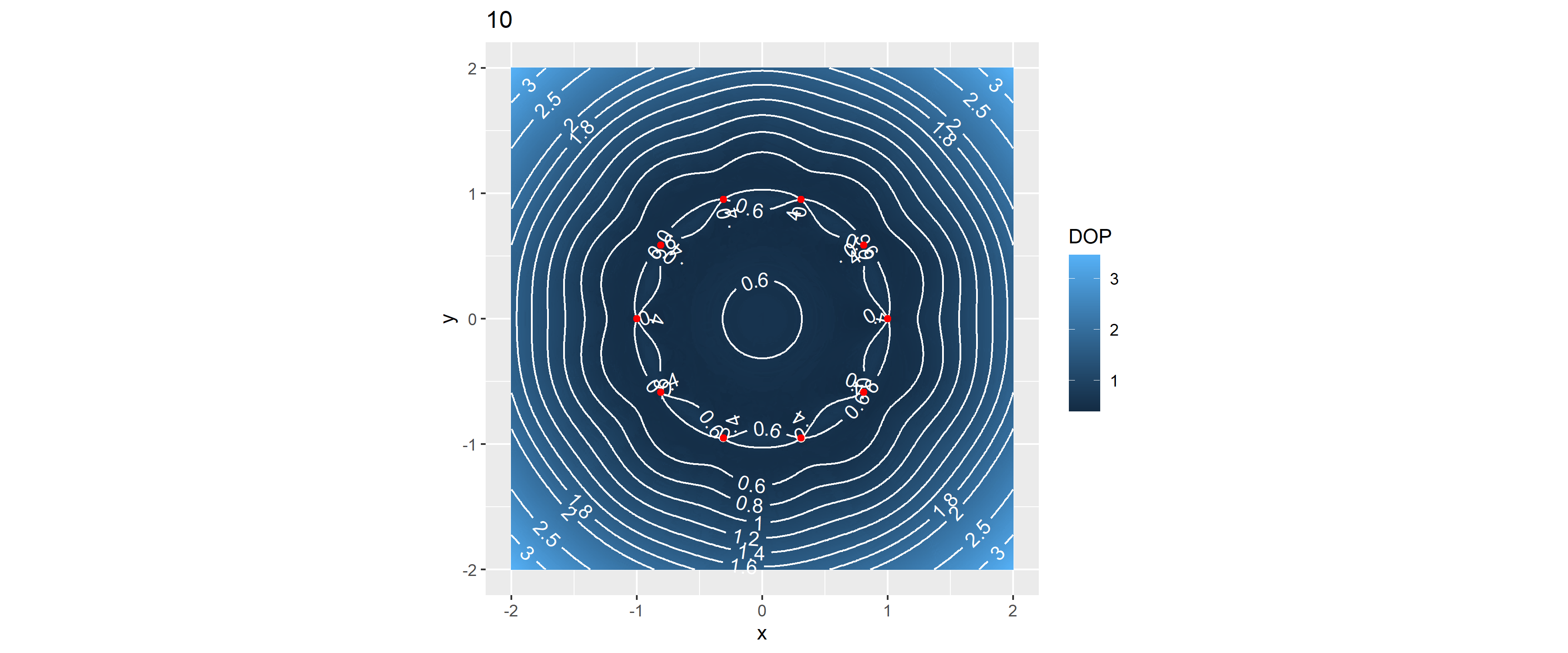
Példaként nézzük meg a különböző számú állomásokat 2-től 10-ig, ha szabályos sokszög-alakban vannak elrendezve:

for(k in 2:10) {
  stations <- PolygonPoints(k)
  
  simgrid$DOP <- DOPgrid(simgrid, stations)
  
  print(ggplot(simgrid[!is.na(simgrid$DOP)&simgrid$DOP<20,], aes(x = x, y = y)) +
          geom_raster(aes(fill = DOP)) +
          geomtextpath::geom_textcontour(aes(z = DOP),
                                         breaks = c(seq(0, 2, 0.2), 2.5, 3, 4, 5), color = "white") +
          geom_point(data = stations, aes(x = x, y = y), inherit.aes = FALSE, color = "red") +
          coord_fixed() + labs(title = k))
}