Unsupervised learning problems such as anomaly detection and clustering are challenging due to the lack of labels required for training embeddings and validating the results. Therefore, it becomes essential to use the right encoding schemes, dimensionality reduction methods, and models. In these types of learning problems, manipulating numerical variables is straightforward as they can be easily plugged into statistical methods. For example, it is easy to find mean and standard deviations in the height of a population.
Categorical variables need to be handled carefully as they have to be converted to numbers. Ordinal categorical variables have an inherent ordering from one extreme to the other, for e.g., sentiment can be very negative, negative, neutral, positive, and very positive. We can use simple integer encoding or contrast encoding for these variables.
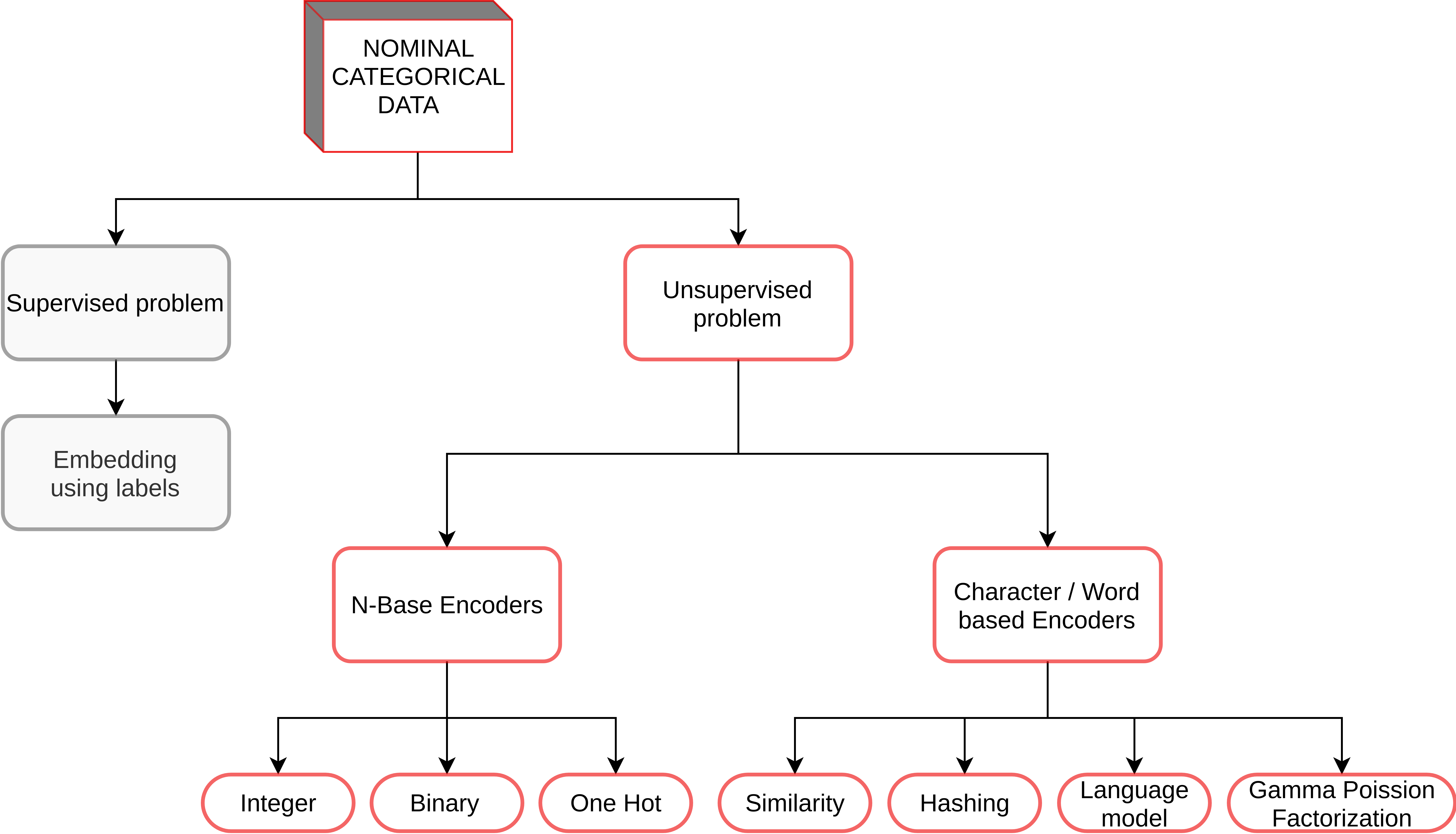
Figure 1: Encoders for nominal categorical variables
In this project, we focus on encoding schemes for nominal categorical variables. Figure 1 summarizes the commonly used encoders for these problems. These variables are particularly challenging because they have no inherent ordering, for e.g., weather can be rainy, sunny, snowy, etc. Encoding to numbers is challenging because we want to avoid distorting the distances between the levels of the variables. In other words, if we encode rainy as 0, sunny as 1, and snowy as 2 then the model will interpret rainy to be closer to sunny than snowy which is not true. A common approach is to use a one-hot encoding scheme. The method works well because all the one-hot vectors are orthogonal to each other preserving the true distances. However, when the cardinality of the variables increases, one-hot encoding explodes the computation. For example, if we have 1000 different types of weather conditions then one-hot would give a 1000 dimension vector. To improve performance, we may choose to reduce dimensions using various forms of matrix decomposition techniques. However, since we cannot go back to the original dimensional space, we lose explainability in this process. Therefore, we search for encoders that optimally balance the trade-off between performance and explainability.
-
After cloning the repository, make sure to initialize and fetch submodules:
git submodule init git submodule update