Implementation based on the segregation model by Thomas C. Schelling, 1971, published in the Journal of Mathematical Sociology, Vol. 1, pp 143-186.
To set-up the grid and distribute the agents, the main idea was to generate the grid on which the action will happen in form of a matrix, such that each agent within that grid is represented by a different number greater than zero, since zero is used to classify empty cells. The method set_up_agents() creates an individual 1d-array for each agent type, with length proportional to the ratio of the agents. Each agent is represented by a different number.
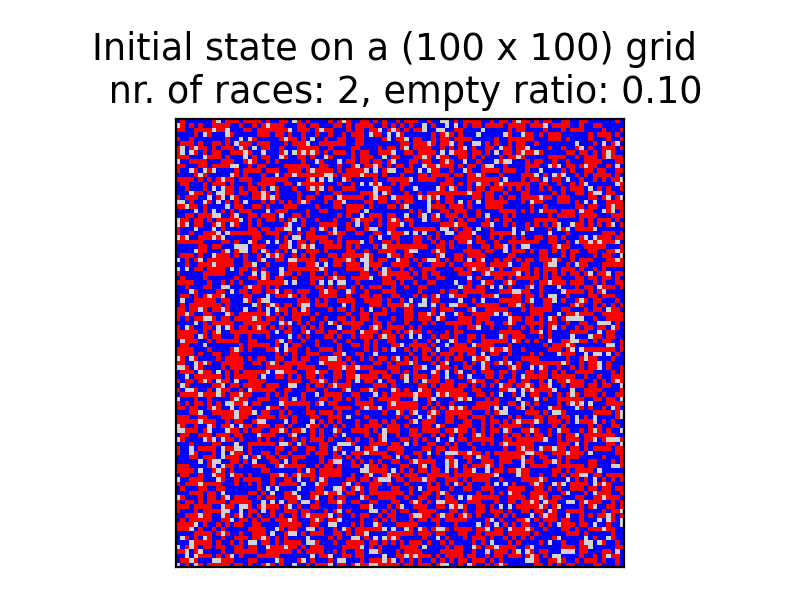
Same was done for the empty cells, where I've created a 1d-array of zeros with length corresponding to the empty_ratio. These arrays are then all being concatenated into one long array, then shuffled to create a random order. Reshaping the array into a into a matrix gives the grid with randomly distributed agents. The first figure displays the initial random state for two different agents and 10% empty cells, randomly distributed on a 100x100 grid, where matrix[row,column].
count_neighbours(row, col) takes a specific position as input, given by parameters row and col, iterates through each cell in the grid and checks if this cell is empty. If true, it will return int(0). If the cell is not empty, then for each agent of the same type found in the neighbourhood around the centre, a counter same will be increased by 1. This loop continues through each agent in the matrix until all are done. If the counter is smaller than the specified threshold needed to achieve happiness, it will return the value -1 for being unhappy, and 1 for being happy otherwise. Setting periodic boundaries means that the agent at one boundary is the neighbour of the agent at the opposite boundary. This periodicity is implemented by using the modulus division to implement a wrap-around at the boundaries:
(col0 + 1) % 10 = 1
(col1 + 1) % 10 = 2
...
(col8 + 1) % 10 = 9
(col9 + 1) % 10 = 0
count\_happiness() iterates over all rows and columns and calculates the happiness of each agent in the matrix by counting the number of neighbours of same type. By doing so, it calculates the happiness factor for each iteration and appends the result to a list. This list is then returned which allows to plot the development of the happiness factor over iterations. Furthermore, it returns a float happiness_factor of how many agents are happy relative to the total number of agents.
According to the specified flag, the method find_unhappy_agent(flag) returns the row and column coordinates of the agents which then will be moved to an empty cell. The agents are chosen according to a flag, which enables sorting the unhappy agents from first to last one, or vice versa, or choosing a random order of unhappy agents.
Given the coordinates of the unhappy agents, it is necessary to find where each agent should move to. The method find_empty_cell(idx_agent, flag) takes the coordinates of the unhappy agent as input and returns the index of the empty cell where the agent needs to be moved. The process of how to choose the empty cell is specified by the flag, it can either find a random empty cell or the nearest empty cell around that unhappy agent, or the matrix can be filled up from from top-down or bottom-up.
Those methods are then applied in another method called move_agents(update_order, moving_order) according to the flags move_agent and update_order. It will take the set of unhappy agents and find the empty cell and move these agents. After the move it will return the number of agents it moved to another cell, in order to keep track of the movements and hence of the convergence for each method.
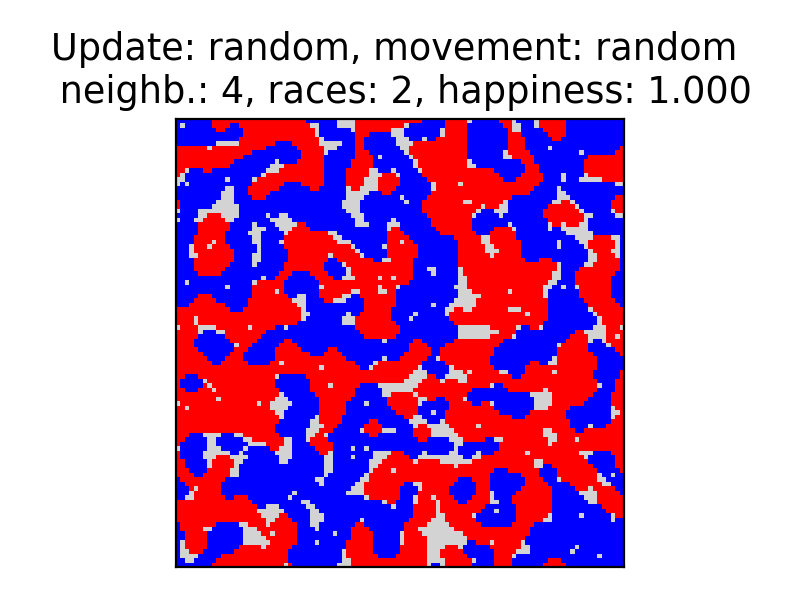
The method run_simulation(update_order, moving_order, strat_switch) runs the simulation until one of the stopping criteria are met. It will stop if there are no more unhappy agents to move, or if for five iterations the number of unhappy agents does not change, or if there is no more significant improvement and the simulation has converged. There is also a possibility to change the strategy of moving the agent mid-simulation. The second figure shows the final state of the agents and displays the seggregation clearly.