Link to hosted project: Fractals with Chaos Game
Made with JavaScript and visualized with the p5.js library
Most general definition:
There are fixed vertices which can be defined by the vertices of a shape, for example a triangle. One vertex is chosen as the starting point then another random vertex is chosen. The midpoint is found between the two points and a dot is drawn there. This midpoint becomes the new starting point and another vertex is chosen at random. The midpoint is then found again and a dot is drawn. A pattern appears as these steps continue. This algorithm creates fractals such as: the Sierpinski Triangle, Sierpinski Carpet and Vicsek Fractal. From a seemingly random algorithm, interesting fractals appear.
With 3 vertices, a Sierpinski Triangle forms:
Other interesting results may arrise when more restrictions are placed, vertices are added and the jump deviates from the midpoint
Restricted Regions
The area in the centre is restricted for these fractals. Points cannot be placed within the central symbol which also prevents them from existing within the smaller ones. This creates a fractal pattern of symbols. Any symbol can be used.
Restricted Movement
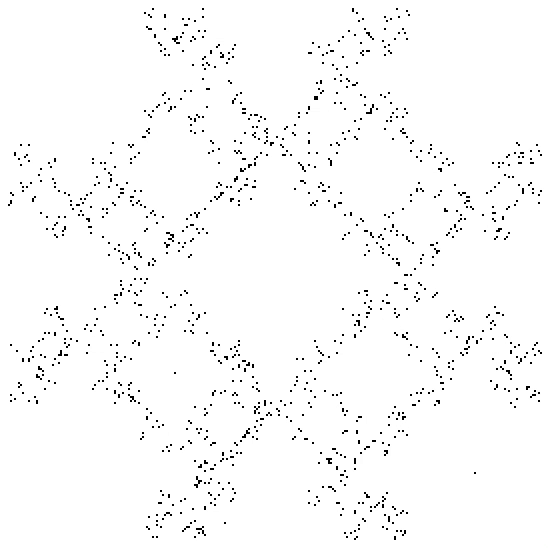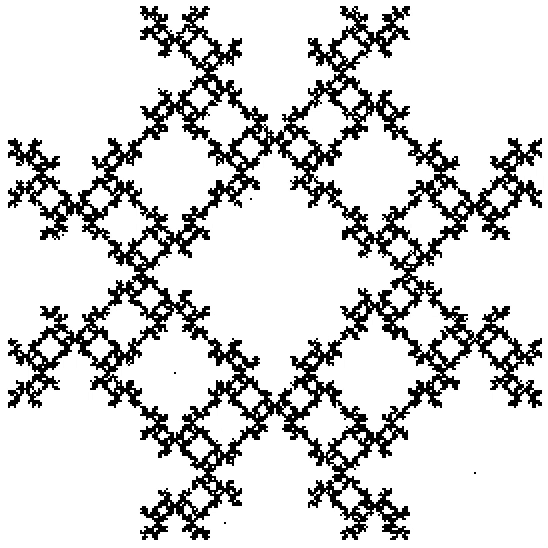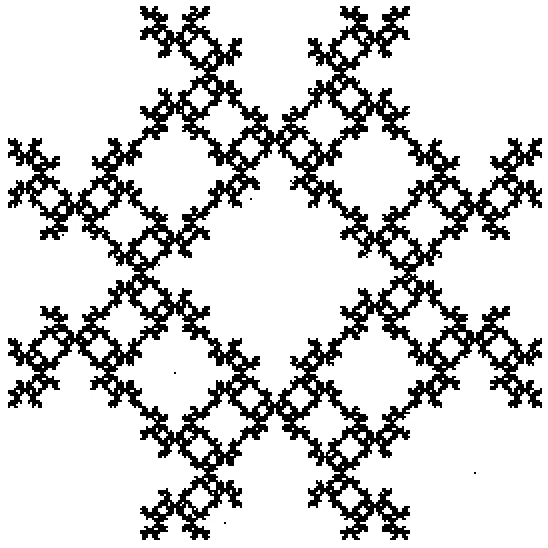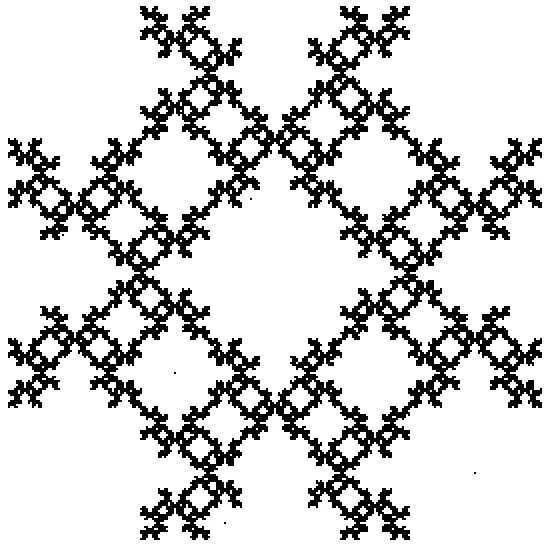
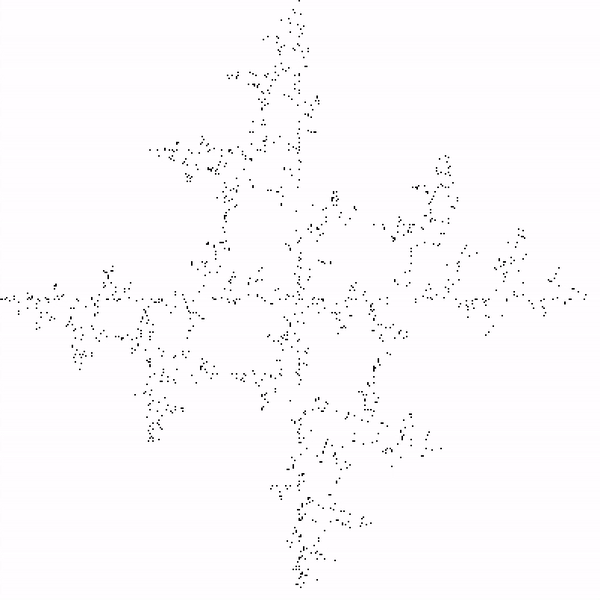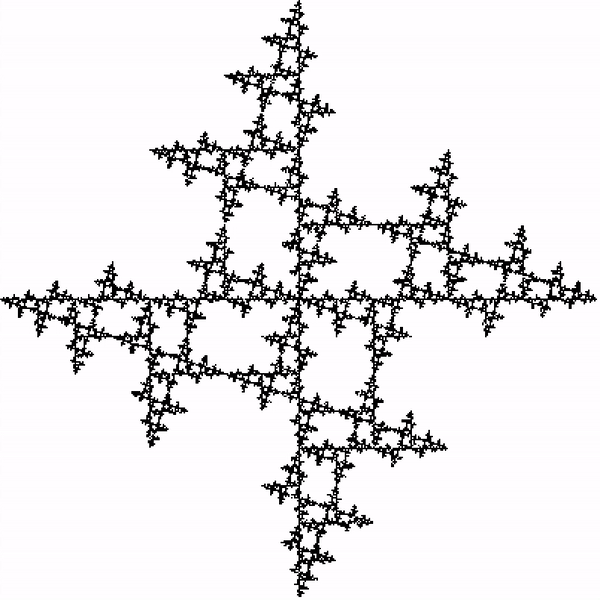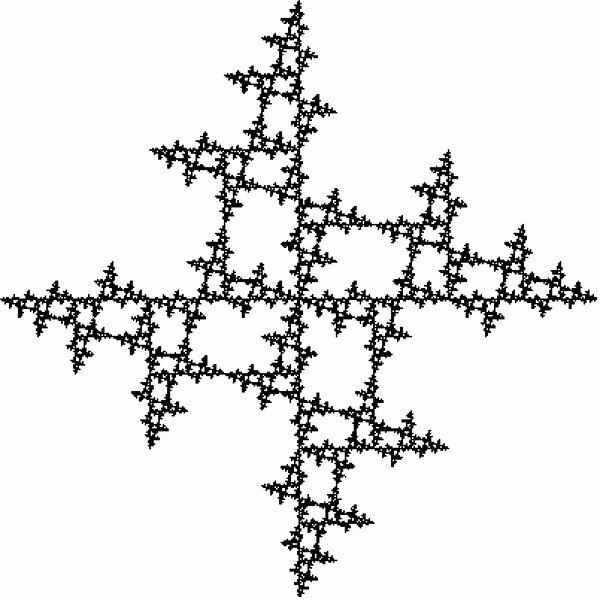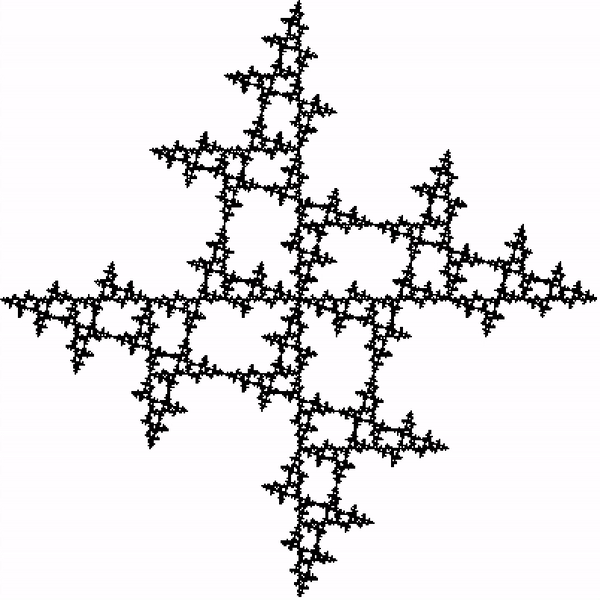
Restrictions are set for what the next point can be based on what the previously chosen point was.
Additional Vertices & Non-midpoint Jumps
New verticies are added and the distance travelled to the next chosen point is not exactly at the midpoint.
Five Vertices are Chosen in the Shape of a Pentagon
On the left, the chosen point cannot be chosen again in the next iteration.
On the right, the point jumps a distance 1 / PHI to the chosen point.
| Result | Restriction |
|---|---|
|
Sierpinski Triangle: 3 vertices |
|
Points cannot be placed within the Nike logo |
|
Same as above but a Pi symbol is used |
|
Same as above but a treble clef is used |
|
The chosen point cannot be chosen again in the next iteration |
|
The chosen point cannot be diagonal from the previous point |
|
The point chosen cannot be ajacent and anti-clockwise to the previous point |
|
Sierpinski Carpet: The point jumps 2/3 of the way to the chosen point The midpoints along the edges are considered vertices |
|
Vicsek Fractal: The point jumps 2/3 of the way to the chosen point The centre is also considered a vertex |
|
The chosen point cannot be chosen again in the next iteration (5 vertices) |
|
The point jumps 1/PHI of the way to the chosen point |