PAMAE: Parallel k-Medoids Clustering with High Accuracy and Efficiency
是SIGKDD2017一篇关于k-medoids并行聚类的论文,论文中作者使用Spark与Hadoop实现算法的并行化,而本项目使用python并行编程模拟MapReduce的并行,对该论文算法的**进行复现。
It is a paper on parallel clustering of k-medoids in SIGKDD2017. In the paper, the author uses Spark and Hadoop to realize the parallelization of the algorithm, and this project uses python parallel programming to simulate the parallelism of MapReduce, and reproduce the idea of the algorithm in this paper.
使用本项目复现的代码对中心数量分别为5、10、15、20的数据集进行聚类的效果图如下(数据集大小为1万)
Using the code reproduced in this project to cluster the data sets with the number of centers of 5, 10, 15, and 20 are as follows (data set size is 10,000)
直接运行如下命令即可,程序会使用默认参数,生成一个数据集,并对该数据集执行聚类算法
Just run the following command directly, the program will use the default parameters to generate a data set, and perform the clustering algorithm on the data set
python pamae.py
也可以指定如下参数: You can also specify the following parameters:
- n_points:生成的数据的个数,默认为10000 (The number of generated data, the default is 10000)
- subset_size:phase 1中采样后子集的大小,默认为100 (The size of the subset after medium sampling, the default is 100)
- subset_num:phase 1中采样的子集的数量 ,默认为5 (The number of subsets sampled in, the default is 5)
- centroid_num:簇中心的数量 ,默认为10 (The number of cluster centers, the default is 10)
python pamae.py --n_points 10000 --subset_size 100 --subset_num 5 --centroid_num 10
程序产生的Phase 1与Phase
Phase 1 and Phase generated by the program
2的聚类结果图,会保存在根目录的results文件夹下,命名方式为"phase[1|2]_数据集大小_采样子集大小_采样子集数量_中心数量",并且在控制台输出每个阶段的的中心集合、耗时、聚类误差等数据
The clustering result map of 2 will be saved in the results folder of the root directory, named as "phase[1|2]_data set size_sampling subset size_sampling subset number_center number", and is under control The platform outputs the central set, time-consuming, clustering error and other data of each stage
聚类就是将数据集划分为多个簇(cluster),每个簇由若干相似对象组成,使得同一个簇中对象间的相似度最大化,不同簇中对象间的相似度最小化。其中k-means与k-medoids是最基础的两种聚类算法
k-means算法选择簇中所有对象的均值作为簇的中心,因此k-means算法实现简单、时间复杂度低,但其对噪声和离群点很敏感
k-medoids算法则是选择离簇均值最近的对象作为簇中心。所以k-medoids算法对噪声和离群点更具鲁棒性,但其时间复杂度却很高。
| k-means | k-medoids | |
|---|---|---|
| 优点 | 实现简单、时间复杂度低 | 对噪声和离群点更具鲁棒性 |
| 缺点 | 对噪声和离群点很敏感 | 时间复杂度高 |
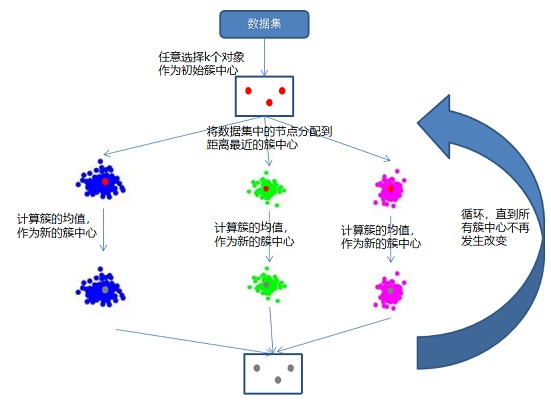
算法简介:k-means算法采用簇中所有对象的均值作为簇中心。给定划分的簇的数量k。随机选择k个对象作为k个簇中心,将剩余对象指派到距离最近的簇,然后重新计算每个簇的新均值,得到更新后的簇中心。不断重复上述步骤,直到簇中心不再发生变化。
k-means算法伪代码如下:
输入:数据集D,划分簇的个数k
输出:k个簇的集合
从数据集D中任意选择k个对象作为初始簇中心
repeat
for 数据集D中每个对象P do
计算对象P到k个簇中心的距离
将对象P指派到与其最近(距离最短)的簇
end for
计算每个簇中对象的均值,以该均值点作为新的簇的中心
until k个簇的簇中心不再发生变化
k-means算法示意图如下:
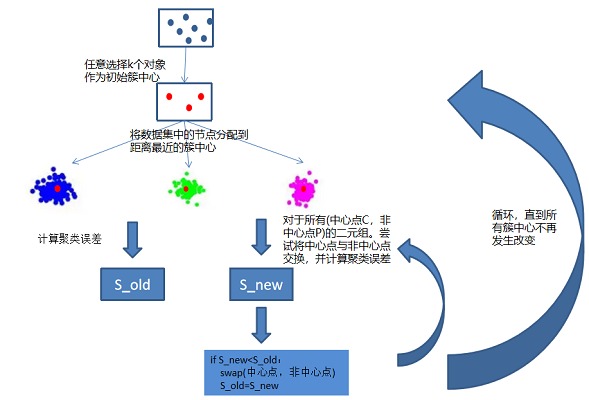
算法简介:PAM算法是k-medoids算法的变种,PAM算法并不是采用簇的均值作为簇中心,而是选择簇中距平均值最近的对象作为簇中心
聚类误差S:所以对象到其簇中心的距离之和
PAM算法伪代码如下:
输入:数据集D,划分簇的个数k
输出:k个簇的集合
从数据集D中任意选择k个对象作为初始簇中心
repeat
把剩余对象分配到距离最近的簇中心
对于所有(中心点C,非中心点P)的二元组。尝试将中心点与非中心点交换,并计算聚类误差
若交换之后聚类误差降低了,则使用该非中心点替换中心点
until k个簇的簇中心不再发生变化
PAM算法示意图如下:
尽管k-medoids具有更好的鲁棒性,但是由于其计算复杂度过高,所以人们用的主要还是k-means算法。有许多研究者尝试解决k-medoids算法的效率问题, 但基本都是以算法准确率作为代价,也就是说现有研究都没能很好地解决k-medoids算法的效率与准确率之间的矛盾。
解决k-medoids算法效率问题的各种举措可以按照以下三个维度进行划分
通过上表,我们可以清楚看到
- global search与entire data的使用可以提高算法的准确率,但会降低算法的效率
- sampled data与local search的使用可以提高算法效率,但会降低准确率
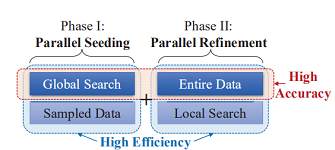
本文尝试在k-medoids的准确率与效率之间找到一个平衡点,于是作者提出了一个基于k-medoids的并行聚类算法(PAMAE),算法分为两个阶段,每个阶段都使用Spark和Hadoop实现并行处理,提高算法的效率:
- 在第一阶段采用sampled data与global search策略
- 在第二阶段采用entire data与local search策略
进行以上组合的原因: global search与entire data策略的使用可以提高算法的准确率,但同时使用,必定会降低算法的效率。而entire data与local search策略可以提高算法的效率,但同时使用,也必定会降低算法的准确率。因此作者在四者的组合中找到了一个平衡点,即sampled data+global search与entire data+local search。
第一阶段的sampled data可以提高算法效率,global search可以提高算法准确率,这是一个高效率+高准确率的组合。
第二阶段的entire data可以提高算法准确率,local search可以提高效率,也是一个高效率+高准确率的组合。
可以发现每个阶段都是高效率+高准确率的组合,PAMAE算法就是通过这种“一快一准”的策略组合,再加上MapReduce的并行处理,以达到高效率和高准确率之间的平衡
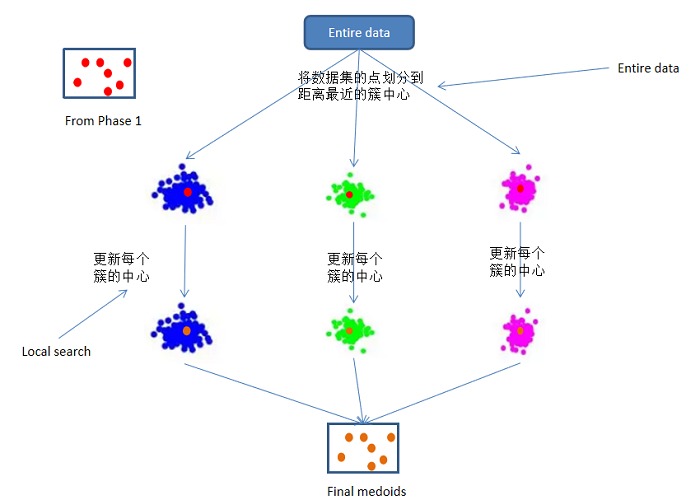
PAMAE算法分为如下两个阶段
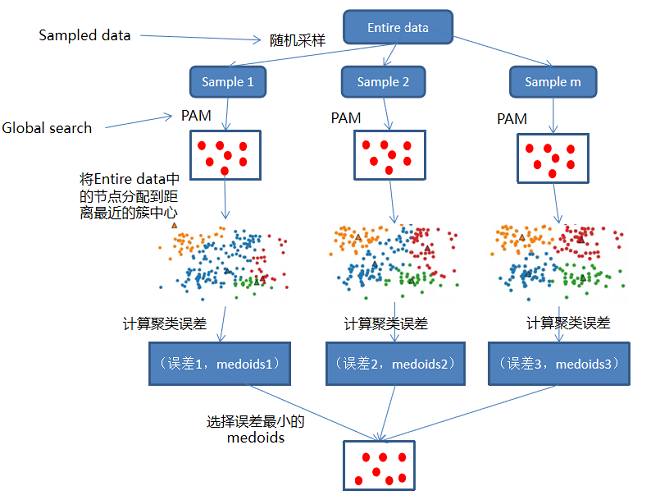
算法**:对整个数据集进行随机采样(sampled data ),生成m个规模为n的子集。然后对m个子集并行执行PAM算法(global search),计算整个数据集的聚类误差,选择聚类误差最小的中心集合
算法流程:
对整个数据集进行随机采样,生成m个规模为n的子集substes
for subset in subsets:
使用global search策略(这里使用PAM算法)找到子集subset的k个簇中心
将整个数据集Entire data的每个数据划分到距离最近的簇中心
计算聚类误差(每个数据点到其簇中心的距离之和)
选择聚类误差最小的一组中心集合输入到Phase2
注:对于for循环里每个子集的聚类与计算聚类误差的操作,是并行的
第一阶段的算法示意图如下:
经过Phase 1的步骤,已经得到了一个近似的聚类中心集合,但是Phase 1中的中心集合是从sampled data中得到的,因此可能与真实的中心还存在一定的偏差,第二阶段就是为了对第一阶段生成的中心集合进行微调
算法**:对于Phase 1获得的中心集合,将整个数据集的数据划分到距离最近的簇中心,然后并行更新每个簇的中心,以达到对簇中心进行微调的目的。得到的就是最终的k个簇中心
第二阶段的算法示意图如下:
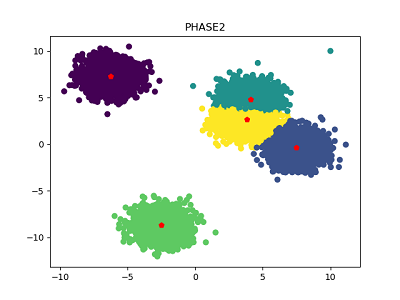
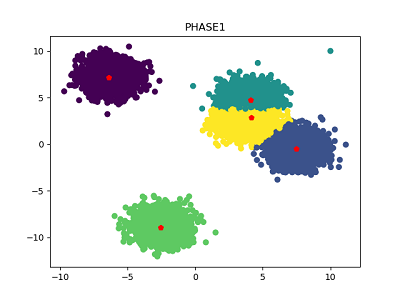
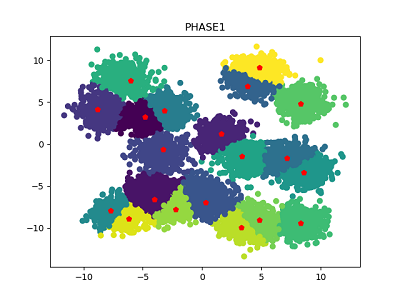
数据集大小为1万,不同中心数量的数据集,第一阶段和第二阶段聚类结果如下所示。可以看到,经过Phase 1得到的聚类效果已经很不错,再经过Phase 2微调之后,聚类效果也确实有所提高。
簇中心数量为5:
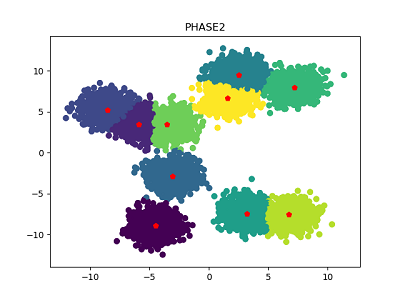
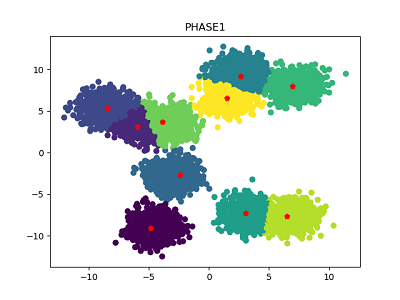
簇中心数量为10:
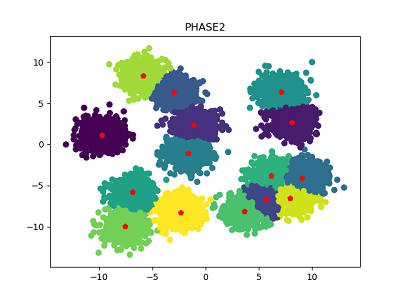
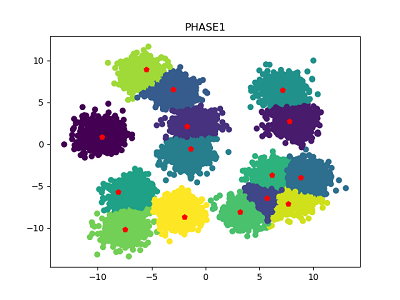
簇中心数量为15:
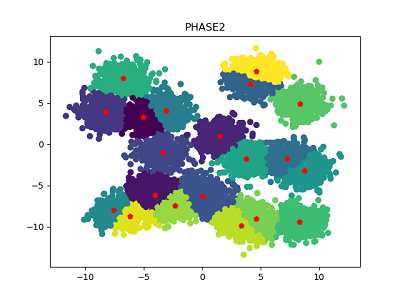
簇中心数量为20:
本项目使用python的并行编程模拟Spark与Hadoop的MapReduce并行计算,运算速度不如MapReduce。由于Phase 1采用的是Global search的策略,运算复杂度较高,当采样子集规模较大时,Phase 1的耗时会增大。