/qhack23_rydberg_graph

Primary LanguageJupyter Notebook

qhack23_project

==================

  • Team name: QuantuMother
  • In this Readme.md for QHack 2023 Quantum kernel methods for graph-structured data , we are including notebooks or pdfs in this repository. This repository will contain the entire project.

Presentation Google slides

Summary:

  1. We implemented the quantum feature map (QEK) in reference [1], in three different approaches:
    1. AWS Braket local simulater. We use Braket's module analog_hamiltonian_simulation for simulating the Rydberg hamiltonian. See demo notebook Braket in demos/ folder.
    2. QuEra Aquila QPU. See train notebook Aquila in TrainingNotebooks/ folder.
    3. PennyLane QML simulator. We also trotterize the analog hamiltonian to digital quantum circuits. The difference here is that we are only preserving geometrically local interaction terms on a graph (see slide 9 in presentation). The resulting kernels are qualitatively different because of missing long-range interactions. See train notebook pennylane in TrainingNotebooks/ folder.
    • We also tried to parrallelize the simulations with SV1 device from AWS. However, we did not find a competitive speed-up compared to the bare PennyLane simulation. See notebook pennylane sv1.
  2. We implemented decompositional quantum graph neural network (D-QGNN) for the same classification tasks. This algorithm decomposes a graph into smaller sub-graphs to reduce the circuit size. See D-QGNN notebook.
  3. We aim to improve the accuracy of QGNN classification by use of CAFQA [4] to get best initialization points for the QGNN ansatz. Since, CAFQA works on classical simulator we wish to demonstrate the symbiosis of classical computing and Quantum computing leading to improvement of QC performance. However, we find that our classical-quantum simulations using QODA has worse performance than PennyLane. See qoda code and slide 16.

Results

  1. We (qualitatively) reproduced results in Ref [1], using a toy model of two simple graphs using Braket simulator. We see QEK's capability of learning an optimal evolution time to achieve maximum distinguishability between two graphs. (Slide 6 )
  2. We implemented a truncated and trotterized version of QEK using PennyLane. We find that with only such short range interactions, no optimal time is present, and therefore we suggest the long-range interactions on Aquila neural atom QPU are important. (slide 9)
  3. To demonstrate QEK's capability beyond the toy model, we ran the same algorithm on two graphs from PTC-FM dataset, and we found optimal evolution time. TODO: We want to finish training and analyzing the full PTC-FM dataset, which is in progress.

Note: the results pickle files are in results folder.

Workflow

  1. Candidate dataset: PTC-FM
  • We picked the PTC-FM dataset, containing graph labels based on carcinogenicity on rats. Being able to compute a binary classification in such compounds is a relevant task either for drug discovery purposes and for health safety concerns. A procedure that works on this dataset should be easily extendible to similar dataset such as MUTAG.
  • See Notebook for loading dataset and Datasets folder

  1. Training algorithm for QEK:

    • We follow ref [1] (which is for running on QPUs), and modify accordingly for approaches 1.1 and 1.3.
      • choose hamiltonian parameter evolution time $t$ (so that all the parameters in the hamiltonian $\Omega(t)$ and $\delta(t)$ will be fixed)
      • determine best initialization points on classical computer using CAFQA
      • use neural atom QPU to simulate the evolution and hence the kernel
      • [todo] postprocess with SVM and proceed with classification
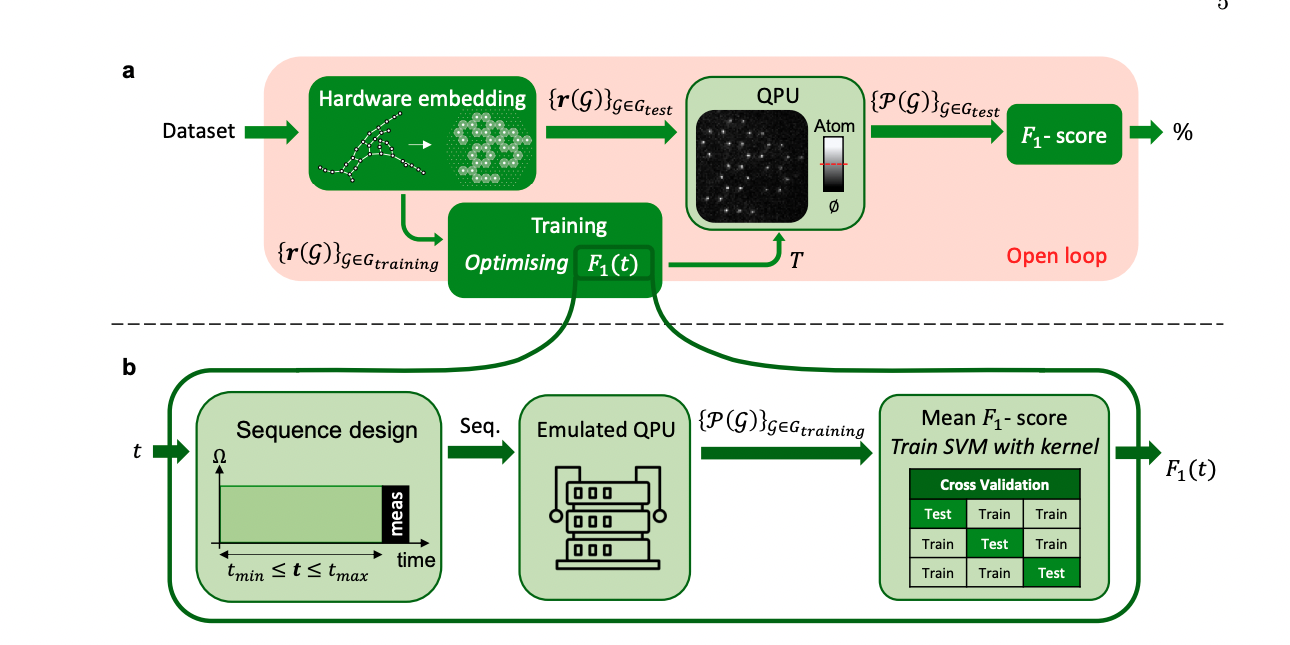
    • see Figure 3: diagram

  2. Training algorithm for QGNN:

    • [todo] to be added.
    • Reason to use CAFQA - VQA's and many QML methods are sensitive to points where they are intialized. If they are initialized at proper points they may reach converegence faster and have a lower risk of getting stuck at local minimas. CAFQA converts the ansatz of VQA and QML methods into clifford circuits which are efficiently simulable on classical computers and obtains the intialization points. Once, we find the best intialization points using CAFQA, VQA's have been shown to reach better accuracies with faster converegcne rates. We envision similar acceleration for our QGNN approach. Useful demo:

Acknowledgements

  • We acknowledge power-ups from AWS, NVIDIA, through which most of the simulations shown were performed. We also thank power-up from IBM.
  • We thank Nihir Chadderwala and Eric Kessler from AWS for their help and debugging assistance.
  • We thank the QHack team for a fun and exciting experience.

References

[1] Main reference for QEK with neural atoms

[2] Another kernel method for graph problem based on Gaussian Boson Sampler---> benchmark

[3] Quantum enhanced GNN

[4] CAFQA

Some related references

Optimization for combinatorial problem

Creating toric code topological state