alkahest is a lightweight, dependency-free toolbox for pre-processing XY data from experimental methods (i.e. any signal that can be measured along a continuous variable). It provides methods for baseline estimation and correction, smoothing, normalization, integration and peaks detection.
- Baseline estimation methods: Linear, Polynomial (Lieber and Mahadevan-Jansen 2003), Asymmetric Least Squares (Eilers and Boelens 2005), Rolling Ball (Kneen and Annegarn 1996), Rubberband, SNIP (Morháč et al. 1997; Morháč and Matoušek 2008; Ryan et al. 1988), 4S Peak Filling (Liland 2015).
- Smoothing methods: Rectangular, Triangular, Loess, Savitzky-Golay Filter (Gorry 1990; Savitzky and Golay 1964), Whittaker (Eilers 2003), Penalized Likelihood (De Rooi et al. 2014)
To cite alkahest in publications use:
Frerebeau N (2024). alkahest: Pre-Processing XY Data from Experimental Methods. Université Bordeaux Montaigne, Pessac, France. doi:10.5281/zenodo.7081524 https://doi.org/10.5281/zenodo.7081524, R package version 1.2.1, https://packages.tesselle.org/alkahest/.
This package is a part of the tesselle project https://www.tesselle.org.
You can install the released version of alkahest from CRAN with:
install.packages("alkahest")And the development version from GitHub with:
# install.packages("remotes")
remotes::install_github("tesselle/alkahest")## Load the package
library(alkahest)alkahest expects the input data to be in the simplest form (a two-column matrix or data frame, a two-element list or two numeric vectors).
## X-ray diffraction
data("XRD")
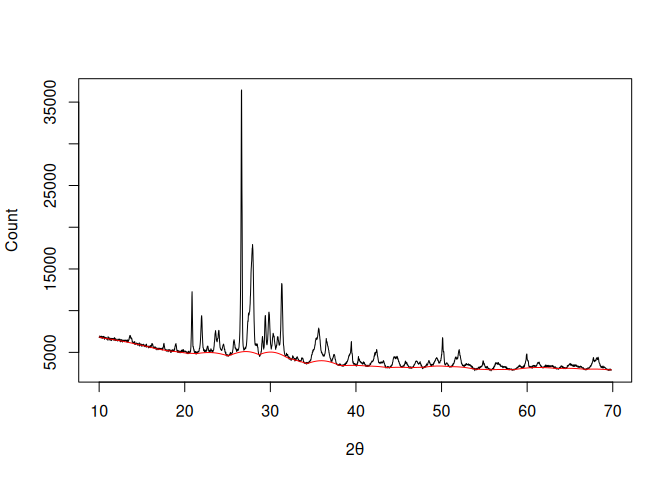
## 4S Peak Filling baseline
baseline <- baseline_peakfilling(XRD, n = 10, m = 5, by = 10, sparse = TRUE)
plot(XRD, type = "l", xlab = expression(2*theta), ylab = "Count")
lines(baseline, type = "l", col = "red")## Correct baseline
XRD <- signal_drift(XRD, lag = baseline, subtract = TRUE)
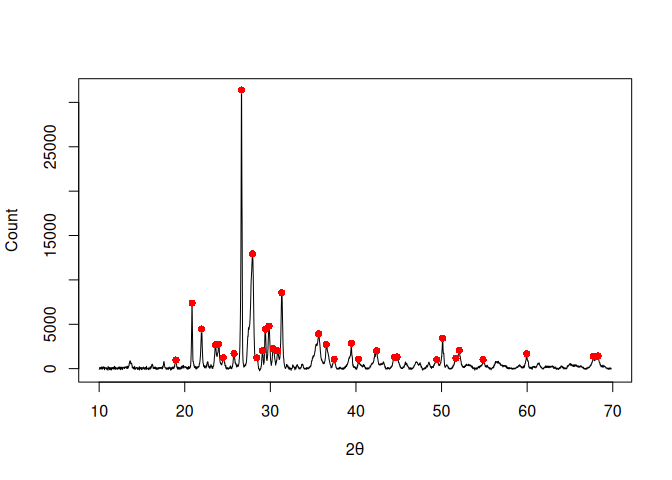
## Find peaks
peaks <- peaks_find(XRD, SNR = 3, m = 11)
plot(XRD, type = "l", xlab = expression(2*theta), ylab = "Count")
lines(peaks, type = "p", pch = 16, col = "red")## Simulate data
set.seed(12345)
x <- seq(-4, 4, length = 100)
y <- dnorm(x)
z <- y + rnorm(100, mean = 0, sd = 0.01) # Add some noise
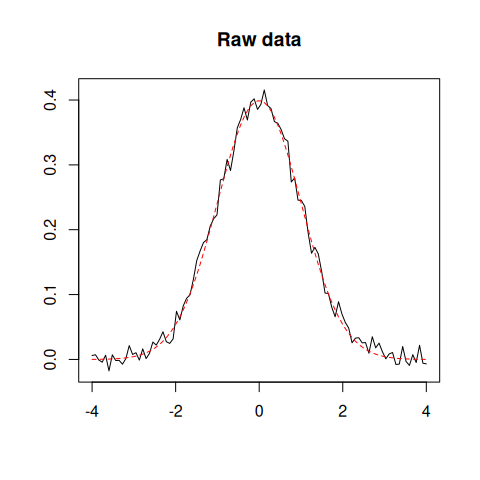
## Plot raw data
plot(x, z, type = "l", xlab = "", ylab = "", main = "Raw data")
lines(x, y, type = "l", lty = 2, col = "red")
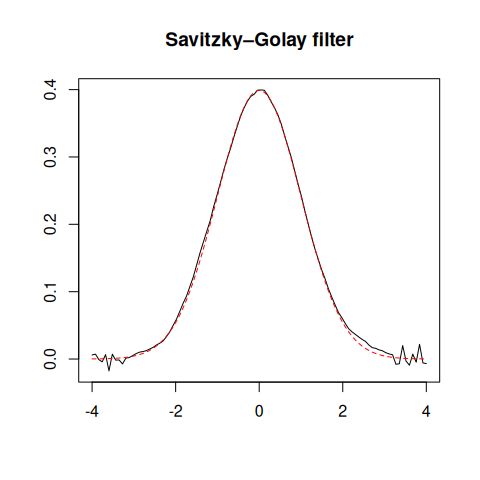
## Savitzky–Golay filter
smooth <- smooth_savitzky(x, z, m = 21, p = 2)
plot(smooth, type = "l", xlab = "", ylab = "", main = "Savitzky–Golay filter")
lines(x, y, type = "l", lty = 2, col = "red")Please note that the alkahest project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.
Barnes, R. J., M. S. Dhanoa, and Susan J. Lister. 1989. “Standard Normal Variate Transformation and De-Trending of Near-Infrared Diffuse Reflectance Spectra.” Applied Spectroscopy 43 (5): 772–77. https://doi.org/10.1366/0003702894202201.
De Rooi, Johan J., Niek M. Van Der Pers, Ruud W. A. Hendrikx, Rob Delhez, Amarante J. Böttger, and Paul H. C. Eilers. 2014. “Smoothing of X-ray Diffraction Data and K α 2 Elimination Using Penalized Likelihood and the Composite Link Model.” Journal of Applied Crystallography 47 (3): 852–60. https://doi.org/10.1107/S1600576714005809.
Eilers, Paul H. C. 2003. “A Perfect Smoother.” Analytical Chemistry 75 (14): 3631–36. https://doi.org/10.1021/ac034173t.
Eilers, Paul H. C., and Hans F. M. Boelens. 2005. “Baseline Correction with Asymmetric Least Squares Smoothing.” October 21, 2005.
Gorry, Peter A. 1990. “General Least-Squares Smoothing and Differentiation by the Convolution (Savitzky-Golay) Method.” Analytical Chemistry 62 (6): 570–73. https://doi.org/10.1021/ac00205a007.
Kneen, M. A., and H. J. Annegarn. 1996. “Algorithm for Fitting XRF, SEM and PIXE X-ray Spectra Backgrounds.” Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms 109–110 (April): 209–13. https://doi.org/10.1016/0168-583X(95)00908-6.
Lieber, Chad A., and Anita Mahadevan-Jansen. 2003. “Automated Method for Subtraction of Fluorescence from Biological Raman Spectra.” Applied Spectroscopy 57 (11): 1363–67. https://doi.org/10.1366/000370203322554518.
Liland, Kristian Hovde. 2015. “4S Peak Filling – Baseline Estimation by Iterative Mean Suppression.” MethodsX 2: 135–40. https://doi.org/10.1016/j.mex.2015.02.009.
Morháč, Miroslav, Ján Kliman, Vladislav Matoušek, Martin Veselský, and Ivan Turzo. 1997. “Background Elimination Methods for Multidimensional Coincidence γ-Ray Spectra.” Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 401 (1): 113–32. https://doi.org/10.1016/S0168-9002(97)01023-1.
Morháč, Miroslav, and Vladislav Matoušek. 2008. “Peak Clipping Algorithms for Background Estimation in Spectroscopic Data.” Applied Spectroscopy 62 (1): 91–106. https://doi.org/10.1366/000370208783412762.
Ryan, C. G., E. Clayton, W. L. Griffin, S. H. Sie, and D. R. Cousens. 1988. “SNIP, a Statistics-Sensitive Background Treatment for the Quantitative Analysis of PIXE Spectra in Geoscience Applications.” Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms 34 (3): 396–402. https://doi.org/10.1016/0168-583X(88)90063-8.
Savitzky, Abraham., and M. J. E. Golay. 1964. “Smoothing and Differentiation of Data by Simplified Least Squares Procedures.” Analytical Chemistry 36 (8): 1627–39. https://doi.org/10.1021/ac60214a047.