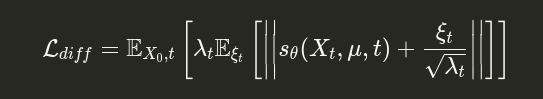This is my (unofficial) implementation of Grad-TTS [1], a Text-to-Speech model based on Probabilistic Diffusion Models. It uses the official implementation [2] as a reference, which in turn relies partly on the code of Glow-TTS [3]. Additionally, HiFiGAN [4] is used as the vocoder in this work, just like the official implementation.
Note: samples of the outputs can be found in data/samples/.
Some machines such as mine associate pip and python to pip2 and python2 respectively. If this is the case, replace pip and python with pip3 and python3 in all of the commands below.
To install the requirements, run
pip install -r requirements.txt
Additionally, if you wish to train the model using the LJSpeech dataset like I did, download it from [5] and untar it to data/LJSpeech-1.1/ so that the model can find it. If you use a different location, modify config.py accordingly.
The project is structured in the following way:
data/has the data related to training and inferencecheckpts/store the model and optimizer checkpoints. In the interest of storage, we only provide model checkpoints of the 100-th and 200-th epochs.hifigan/andhifigan-checkpts/contain the hifigan code and checkpoint(s).utils/globals.pyhas the global variables that are not configuration parameters and are used by many modules. On the other handutils/data.pyhas functions related to loading, preprocessing and bundling of data intoDataset/DataLoaders.models/alignment/has the cython module for maximum alignment search, heavily referenced on the official equivalent.models/models.pydefines the various models that are either used directly or indirectly via other models.models/training.pyexposes functions to instantiate and train the above models, whilemodels/inference.pyhas a function to do the entire conversion of text-to-speech.- Finally,
main.pyties everything together and interfaces with the user, who can changeconfig.pyto change various aspects of training and/or inference. notebook/contains the original notebook which I used for this work.
After downloading the LJSpeech dataset and placing it in data/LJSpeech-1.1 and changing the configuration in config.py if you want, you can run
python main.py --train
to train. This will by default save checkpoints, resume from last checkpoint and launch a tensorboard instance. If you want to convert text to speech and not train the model, LJSpeech need not be downloaded. Simply run
python main.py --tts <string-to-convert> --out <path-to-output>
or
python main.py --file --tts <path-to-in-file> [--out <path-to-output>]
in the latter case, if an output path is unspecified, X.txt's output will be saved to X.wav, for the input X.txt.
While a complete description of the model is infeasible to include in such little space (and readers are referred to [1]), here is the rough idea (entirely based on the paper):
Consider a member of a distribution of "objects" (vectors), such as an image, and subjecting it, called
-
$0$ outside a window of $W $ on either size - unevenly distributed inside the window - the exact weightage is learnt, and is different across heads and across $Q,K,V $ s.
Then, a duration predictor (a simple CNN) predicts factors by which to inflate each frame of the output above. This in turn is taken to be $\mu $ above. Further $\Sigma = I $ is assumed for simplification. Then the reverse ODE is solved to produce the mel-spectrogram of the target audio. The one unknown in it, namely $\nabla \log p_t(X_t) $ is predicted by a UNet [8]-style network at each step of solving the ODE (we use Euler's method). The final mel-spectrogram is converted back to audio using a vocoder. HiFiGAN [4] works well for this. All models contain a combined total of 14.84M trainable parameters.
Acknowledgements: The text encoder uses CMUDict [9, 10] to map words into phonemes, which are then passed through an embedding layer and a pre-net (simple CNN with Mish [11] activations).
The loss function has three components. First, during training, we get the gold-truth alignment between text and speech using Monotonic Alignment Search (a simple Dynamic Programming algorithm, see [3]) - this gives us the "ground truth" values that the Duration Predictor should have output for each position. This is turned into an MSE loss term: $$ d_i = \log \sum_{j=1}^F \mathbb{I}_{{A^*(j)=i}},\hspace{1.1em}i=1,2,\cdots,L, $$
(extra line just because GitHub markdown LaTeX rendering is super buggy and needs specific things like a space before ending dollar but not after the opening one, and no consecutive full-line equations, plus an empty line after the double dollar full line equation) $$ \mathcal{L}_{dp} = \text{MSE}(\text{DP}(\text{sg}[\tilde{\mu}, d])) $$
The prior or encoder loss enforces the text encoder's output after inflation by the duration predictor to be close (enough) to the actual mel-spectrogram: $$ \mathcal{L}{enc} = -\sum{j=1}^F \log \varphi(y_j;\tilde{\mu}_{A(j)}, I) $$
There is also a loss term to ensure that the gradient predictions are correct. First, with $\Sigma = I $ at $t=T $ as we take it, the covariance matrix at time $t $ is just $\lambda_tI $ with $$ \lambda_t = 1 - \exp\left(-\int_0^t \beta_sds\right) $$
and so $X_t $ is effectively sampled from a guassian of the form
The final loss term is (unfortunately, the GitHub markdown renderer is awful, so if I type out the equation, it interprets underscores following closing braces as italicization; I tried adding invisible characters after mathbb and mathcal to remedy it, but the only way to do is phantom{} or vphantom{} in LaTeX, which themselves take input through curly braces; so here's an image instead)
The graphs below show the training losses w.r.t to time
Note that the diffusion loss fluctuating a lot and apparanetly not decreasing is expected, as noted in [1] .
I originally implemented the code on Google Colab, and then ported it over to a "traditional" repository format, so some errors may have crept in, though I did run the code on my PC to verify it. If you find any bugs, I'd love to hear from you and fix it ASAP.
[1] Grad-TTS: A Diffusion Probabilistic Model for Text-to-Speech, ICML 2021, Vadim Popov, Ivan Vovk, Vladimir Gogoryan, Tasnima Sadekova, Mikhail Kudinov
[2] Grad-TTS official implementation, last acessed June 16, 2022.
[3] Glow-TTS: A Generative Flow for Text-to-Speech via Monotonic Alignment Search, NeurIPS 2020, Jaehyeon Kim, Sungwon Kim, Jungil Kong, Sungroh Yoon
[4] HiFi-GAN: Generative Adversarial Networks for Efficient and High Fidelity Speech Synthesis, NeurIPS 2020, Jungil Kong, Jaehyeon Kim, Jaekyoung Bae
[5] The LJSpeech Dataset, last accessed June 16, 2022
[6] Reverse-Time Diffusion Equation Models, "Stochaistic Processes and their Applications 12" (1982), Brian D.O. Anderson
[7] Score-Based Generative Modeling through Stochastic Differential Equations, ICML 2021, Yang Song, Jascha Sohl-Dickstein, Diederik P. Kingma, Abhishek Kumar, Stefano Ermon, Ben Poole
[8] U-Net: Convolutional Networks for Biomedical Image Segmentation, MICCAI 2015, Olaf Ronneberger, Philipp Fischer, Thomas Brox
[9] CMUDict, last accessed June 16, 2022.
[10] CMUDict (pip), last accessed June 16, 2022.
[11] Mish: A Self Regularized Non-Monotonic Activation Function, BMVC 2020, Diganta Misra