Automated dialog systems often need to handle spoken numbers. In particular, a caller may provide a phone number using speech. Then, the documented phone number needs to be validated. During this procedure we may face number ambiguities. For example a caller may pronounce "Seventy Five" which can be translated as "70 5" or "75". In this application, we handle such possible ambiguities.
The programm has two main functionalities. The firsto one, which we will refer to as Basic, is to identify if a given number is a valid Greek phone number. A valid greek phone number obey one of the following rules:
- starts with "003069" or "00302" and contains 14 digits.
- starts with "2" or "69" and contains 10 digits.
The second functionality, called Advanced, identifies the several ambiguities, and checks, if the resulted interpretations are valid Greek phone numbers. The source files of this application are located in the src folder. For execution run the following:
python natural_numbers_interpretation.py -numbers " "," " | -file filename -method a|b
The argument options are the following:
- -n NUMBERS, --numbers NUMBERS. Input phone numbers as string. If multiple seperated by ",".
- -f FILE, --file FILE Input file of numbers. Seperate Different numbers by "\n".
- -m METHOD, --method Method {a,b}. Option b for Basic a for Advanced. Default is advanced.
Example1
python natural_numbers_interpretation.py -n "210 200 20 3 876","69 45 700 24" -m a
Example 2
python natural_numbers_interpretation.py -f phonenumbers.txt -m a
Example 3
If no input via the command line is provided, the application will ask the user for providing with a phone number.
Acceptable inputs are sequences of numbers sperated by a space character. Each sequence must be at most a 3 digit number. If the user provides input that violates this rules, the input will not be processed.
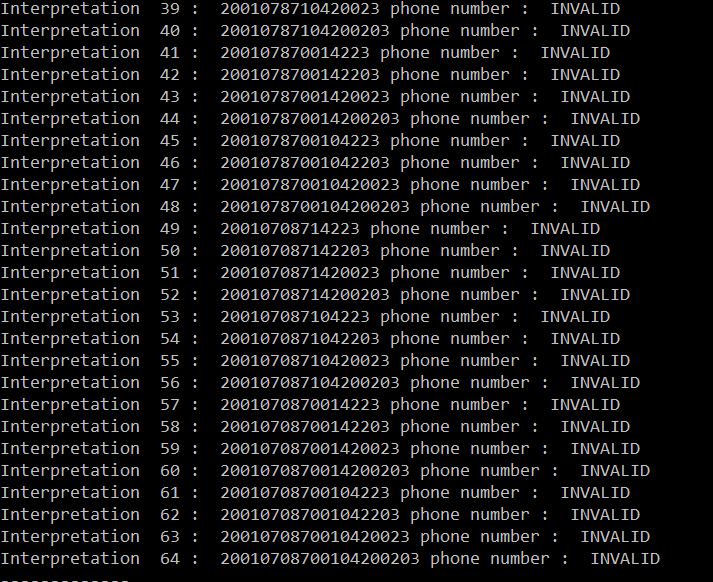
Below we show a part of the output produced using the file _phonenumbers.txt:
The project is implemented in two source files. A python module named "natural_numbers_interpretation.py" contains the main functionality. In this file the arguments are parsed, and the valid inputs are processed by the chosen method level (basic or advanced). Each valid input is then inited and set as a PhoneNumber Class object. This class is implemented in the phone_number.py module. Thiss class represent a phone number, and contains class variables needed to validate if it is a phone number, and find the possible interpratations of the ambiguities that it may contain.
A PhoneNumber object has the following properties:
- name : full_number_str , type : string , description : The input string
- name : full_number_tokens, type: list, description : List of the sequences
- name : number_prefix_str, type: string , description : The prefix if present = "0030"
- name : number_suffix_str, type: string , description : The suffix string
- name : number_suffix_tokens, type: list, description : List of the suffix sequences
To identify if a number is a valid greek phone number we parse the concatanated number(prefix and suffix) and check if it matches the rules.
At this part we will explain our approach regarding the identification of the number ambiguities. To do so we handle the variable number_suffix_tokens, which is the list containing all the subsequent sequences of the input (except prefix "0030"). The main concept is that we perform expands and merges in the sequences. For example, the sequence "710" can be expanded to "700 10". A merge of two sequences "60 5" will produce the "65" ambiguity. The challenging part of this process was combining effectively possible ambiguites, and ambiguities that could be a combination of these two. To overpass this we concluded that the most effective approach which produces all the possible ambiguities is performing at first the merging process, and then the expands on the merged items. More particular:
- We first perfom the merging process. At this step, we manipulate the sequences (tokenized by splitting in the space chars). The class method that handles this procedure is a private method named __first_level_merge. The input is the list of subsequent sequences, and we compute all the possible merges, by using the __merge function with input two consequent strings. Two strings are merged if the number of trailing zeroes of the first string is at least as many as the length of the second string. The result of this procedure is a new list of sequences with each seqence be at most a 3-digit number.
- Following the above, we perform the expands of a sequence. This is performed in the private method of the class __expands . This function is implemented recursively. Any 1-digit number, or 2-digit of special case1 will not be expanded. In any other case we add the expected zeroes to expand the number. This function is applied on the previously computed merges in the first level. By following this approach, we can produce all possible expands, that can occur from merges.
- To find all the possible combinations of the interpretations, we compute the cartesian product of each expanded result2.
- 1-digit sequence cannot expand;
- 2-digits sequence spawns at most one new interpretation
- if the sequence contains the digit `0' it cannot be expanded;
- 3-digits sequence spawns at most three new interpretations
- if the sequence contains the digit `0' twice, it cannot be expanded;
- if the sequence contains the digit `0' once, it spawns at most one new interpretation (see 2-digit case);
After having the shortest version of the input sequence (after the initial merge) we can compute the total number of possible interpretations.
Let
be the number of different sequences that cannot be expanded;
be the number of different 2-digits and 3-digits sequences that spawns one new interpretations; and
be the number of different 3-digits sequences that spawns three new interpretations. The total number of interpretations is equal to:
In order to test the performance of our application we provide Unit Test results. This has been achieved by using python's standard built in library unittest. We have implemented the unit tests in the tests folder of our project. To run these test one can navigate in the corresponding folder and input the following:
python test_phone_number.py
We have created test cases for the basic, and the advanced method level of our application.3 The test cases we reproduced are the following input numbers:
- "0 0 30 69 700 24 1 3 50 2"
- "200 20 3 710 4 5"
- "2 10 69 30 6 6 4"
- "214 65 2 000 1"
Which produce the following output :
The test module for the above cases passes. We chose these cases carefully, as they contain some peculiarites. We prove that all zeroes sequence does not expand ore merge. Also in the second use case we can merge three sequences (200 20 3 => 223), and prove that it allso works correctly. In general the various inputs we tested all produced the correct result.
We also ran more tests that had more complex output but were not validated automatically.
This application was implemented using the Anaconda distribution of python 3.7 and conda 4.8.2. In our source files we have included numpydocstring comments as documentation of the crucial files.
Footnotes
-
x0,00,x00,0x0,00x,0x,x,11,12 dont expand in greek pronunciation. ↩
-
We get the unique values, as the cartesian product contains duplicates. ####Number of Interpretations Given the fact that the input sequences are at most triplets (i.e., a sequence contains an at least 3-digit number) we have the following: ↩
-
We did not perform unit test for the input, as it is out of the scope of this assignment. ↩