Mirrors (Code Assignment from Ensign )

1. Problem

Safe Ltd. is a company that manufactures high-quality safes. Its latest invention is an optical closure mechanism that uses a laser beam passing through a rectangular grid with several mirrors.

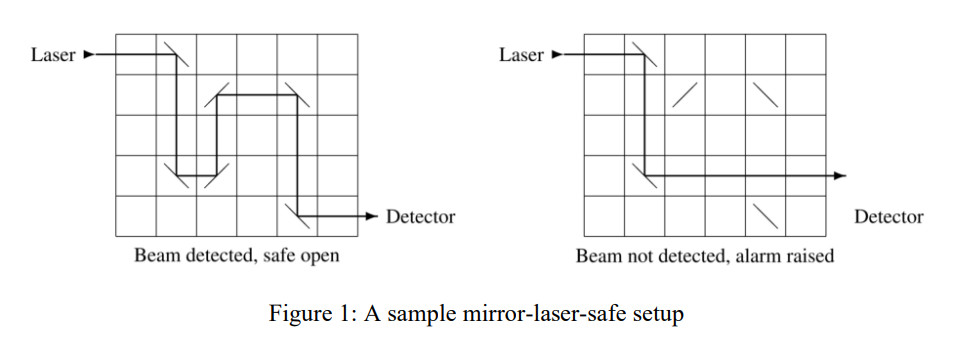
When the laser is activated, a beam enters the top row of the grid horizontally from the left. The beam is reflected by every mirror that it hits. Each mirror has a 45 degree diagonal orientation, either / or \. If the beam exits the bottom row of the grid horizontally to the right, it is detected and the safe opens (see the left side of the figure above). Otherwise the safe remains closed and an alarm is raised.

Each safe has a missing mirror, which prevents the laser beam from traveling successfully through the grid (see the right side of the figure above). The safe has a mechanism that enables the user to drop a single mirror into any empty grid cell. A legitimate user knows the correct position and orientation of the missing mirror (/ in row 4 column 3 above) and can thus open the safe. Without this knowledge the user has to guess correctly, which can be difficult for safes with large grids.

Your job is to determine if particular safes are actually secure. A secure safe does not open right away without inserting a mirror, and there is at least one valid location and orientation for the missing mirror. There may indeed be multiple such locations and orientations.

Input

Each test case describes a single safe and starts with a line containing four integer numbers r, c, m, and n (1 ≤ r, c ≤ 1000000 and 0 ≤ m, n ≤ 200000). The mechanisms grid has r rows and c columns.

Each of the next m lines contains two integer numbers ri and ci (1 ≤ ri ≤ r and 1 ≤ ci ≤ c) specifying that there is a / mirror in row ri column ci . The following n lines specify the positions of the \ mirrors in the same way. The m + n positions of the mirrors are pairwise distinct.

Output

For each test case, display its case number followed by:

0 if the safe opens without inserting a mirror.
k r c if the safe does not open without inserting a mirror, there are exactly k positions where inserting a mirror opens the safe, and (r, c) is the lexicographically smallest such row, column position. A position where both a / and a \ mirror open the safe counts just once.
impossible if the safe cannot be opened with or without inserting a mirror.

Problem Analysis, Approach and Implementation

To solve this problem, we need to divide the problem into several parts.

1. Firstly we need to check that the laser beam is safe open or alarm raised.

To check this problem we need make the laser beam to travel forward in code LaserWork.Laser.laserBeam_travel_forward (Left to Right).
But the grids input variables are r, c, m and theses can be n (1 ≤ r, c ≤ 1000000 and 0 ≤ m, n ≤ 200000). So if we just move 1 grid cell at a time, it will take more processing time. So we need to record the input pairs (row, col and mirror status) and make sure to only travel in inputs pairs. For better understanding please see the following steps:
In Forward travel step-3: the laser beam pass to the end point (col) from row 4. And this define as alarm raised and we need move to next process.

2. Secondly we need to search the where we should add the mirrors.

To know the mirrors locations, we need make travel backward to the crossing places. We recorded need horizonal and vertical lines from forward travel. And also we need recorded horizonal and vertical lines from backward travel.

Only horizonal lines can cross vertical lines. So I searched intersection points between horizonal-lines-from-backward-travel and vertical-lines-from-forward-travel . And also searched intersection points between horizonal-lines-from-forward-travel and vertical-lines-from-backward-travel . As a result is show below:

3. Handling worst case and lexicographically smallest point

Let's consider about the worst case as show below.

In this case we need a lot comparison between horizontal-backward and vertical-forward. And also horizontal-forward and vertical -backward . If we search the intersections in all these, can it be take a lot of times.
To avoid time consuming we need to used some arrange tree algorithm. In here we use binary search tree with row key.
But according to the question. We have to choose lexicographically smallest row and column position. So we choose (1,5) that the result will be follow:

How to Run

add input data to "input.txt" and save .
python main.py

References:

Binary Search Tree

tharhtetsan/Safe_mirror