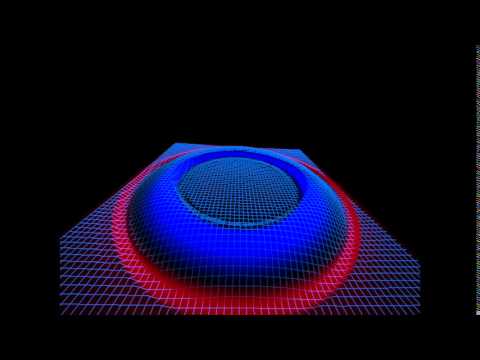
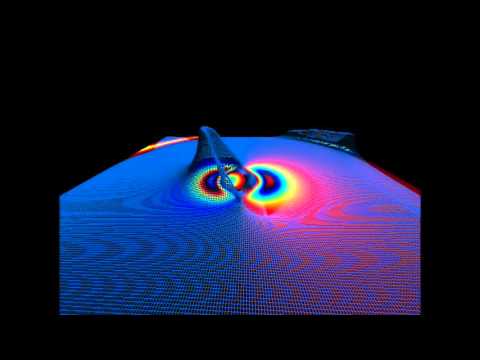
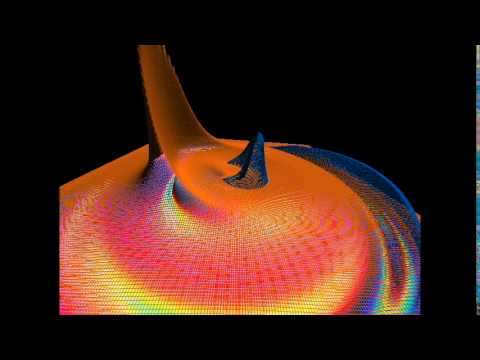
A finite volume solver based on hyperbolic formalisms.
Works in 1D, 2D, and 3D.
Simulates Euler equations, SRHD, Maxwell, and ADM formalism (Bona-Masso) numerical relativity. Almost got MHD working.
Euler is simulated via Burgers, HLL, HLLC, Roe.
SRHD via Roe.
Maxwell via Roe.
ADM Bona-Masso via Roe.
MHD, I'm working on a Burgers, HLLC, and Roe ... though none are working yet.
Slope limiters are working on all Burgers and Roe solvers.
Support for Periodic, Mirror, and Free-Flow boundary methods.
Self-gravity option for Euler and MHD equation solvers.
Might get around to CG or GMRes method of Backward Euler implicit integration.
C++
- Common: https://github.com/thenumbernine/Common
- CLCommon: https://github.com/thenumbernine/CLCommon (depends on OpenCL)
- ImGuiCommon: https://github.com/thenumbernine/ImGuiCommon (depends on ImGui listed below)
- GLApp: https://github.com/thenumbernine/GLApp (depends on OpenGL listed below)
- SDLApp: https://github.com/thenumbernine/SDLApp (depends on SDL2 listed below)
- Tensor: https://github.com/thenumbernine/Tensor
- Profiler: https://github.com/thenumbernine/Profiler
- Image: https://github.com/thenumbernine/Image (depends on LibPNG, listed below)
- GLCxx: https://github.com/thenumbernine/GLCxx
- LuaCxx: https://github.com/thenumbernine/LuaCxx (depends on Lua/LuaJIT, listed below)
Lua
external:
- ImGui v1.48: https://github.com/ocornut/imgui
- Lua (used by LuaCxx, check that for instructions on building against either), use either one:
- 5.x: https://www.lua.org/
- LuaJIT: http://luajit.org/
- SDL2 v2.0.3 (used by GLApp): https://www.libsdl.org/
- LibPNG v1.7.0-beta6 (used by Image): http://www.libpng.org/pub/png/libpng.html
- OpenCL v1.2. If your dist doesn't include the cl.hpp header (coughApplecough) then just put it in the CLCommon/include/OpenCL/ folder
- OpenGL
Hydrodynamics:
- Duellemond, 2009. Lecture on Hydrodynamics II http://www.mpia-hd.mpg.de/homes/dullemon/lectures/hydrodynamicsII/
- Masatsuka, I Do Like CFD. http://www.cfdbooks.com/cfdcodes.html
- Toro, Eleuterio F. Riemann Solvers and Numerical Methods for Fluid Dynamics - A Practical Introduction. Springer, Germany, 1999. 2nd Edition.
- http://people.nas.nasa.gov/~pulliam/Classes/New_notes/euler_notes.pdf
Electromagnetics:
- Trangenstein "Numerical Simulation of Hyperbolic Conservation Laws"
Numerical Relativity- ADM, BSSN, etc:
- Alcubierre, Miguel. Introduction to 3+1 Numerical Relativity. Oxford Science Publications, Oxford, 2008.
- Baumgarte, Shapiro. Numerical Relativity: Solving Einstein's Equations on the Computer, 2010.
Stellar Schwarzschild initial conditions:
- Misner, Thorne, Wheeler. Gravitation, 1973
SRHD:
- Marti, J. M. and Muller, E. Numerical Hydrodynamics in Special Relativity Living Reviews in Relativity 6 (2003), 7 http://relativity.livingreviews.org/Articles/lrr-2003-7
- Sheck, Aloy, Marti, Gomez, Muller Does the plasma composition affect the long-term evolution of relativistic jets? Monthly Notices of Royal Astronomical Society 331, 615-634 2002.
- Anton, Luis; Zanotti, Olindo; Miralles, Juan; Marti, Jose; Ibanez, Jose; Font, Jose; Pons, Jose. Numerical 3+1 General Relativistic Magnetohydrodynamics: A Local Characteristic Approach February 2, 2008 https://arxiv.org/abs/astro-ph/0506063
HLLC:
- http://math.lanl.gov/~shenli/publications/hllc_mhd.pdf
- http://marian.fsik.cvut.cz/~bodnar/PragueSum_2012/Toro_2-HLLC-RiemannSolver.pdf
MHD Roe:
MHD initial conditions:
- Brio, M. & C.C. Wu, "An Upwind Differencing Scheme for the Equations of Ideal Magnetohydrodynamics", Journal of Computational Physics, 75, 400-422 (1988). The test is described in Section V.
Runge Kutta & TVD RK:
- http://www.ams.org/journals/mcom/1998-67-221/S0025-5718-98-00913-2/S0025-5718-98-00913-2.pdf
- http://lsec.cc.ac.cn/lcfd/DEWENO/paper/WENO_1996.pdf
linux packages required:
- opencl-clhpp-headers
- cimgui
- Image requirements:
- libcfitsio-dev
- libtiff-dev