_
\`*-. _ __ _ _
) _`-. | |/ / | | (_)
. : `. . | ' / __ _| |_ ___ _ _ _ __ ___ _
: _ ' \ | < / _` | __/ __| | | | '_ ` _ \| |
; *` _. `*-._ | . \ (_| | |_\__ \ |_| | | | | | | |
`-.-' `-. |_|\_\__,_|\__|___/\__,_|_| |_| |_|_|
; ` `.
:. . \ Remember:
. \ . : .-' . Encryption provides secrecy,
' `+.; ; ' : not authentication or integrety.
: ' | ; ;-.
; ' : :`-: _.`* ; Martin Azaël && Gobinet Théo
.*' / .*' ; .*`- +' `*'
`*-* `*-* `*-*'
Katsumi is an interactive cryptographical tool.
Designed on Arch Linux and Windows 10 for Linux and Windows operating systems.
Black was used to check the formatting of our code:
sudo black Katsumi/
Carried out in accordance with PEP8
Read this in other languages: French
It is a school cryptography project carried out at the UTT for the GS15 subject in the Fall 2020 (A20). For more information about this subject, click here (it's in French).
-
Clone the repository then go to the eponymous folder and launch "katsumi.py" with python 3.
-
No requirements.txt needed . Everything works without the need for additional libraries. A native installation of python3 is enough !
This project was initially devoted to the development of a modified version of Kasumi's symmetric encryption algorithm, then to the generation of a public/private key pair to finally gather all the acquired knowledge and simulate a blockchain.
The source code is ordered as follows:
- The "core" folder contains the core of the program. Everything related to symmetric, asymmetric and hash-based encryption methods (i.e. the BlockChain).
- The "processing" folder which contains all outputs of the program destined for the user (i.e. public/private keys, digital signatures and encrypted things).
- The "resources" folder contains all the largest code files. This is where most of the primary functions reside.
-
The primitive polynomial of the binary extension field GF(2) of degree 16 was found online and hard-coded into a config file
-
To make it easier to handle the inverses in the Galois fields, we have pre-recorded in memory the inverses of the Galois field degree 16 (itself written in raw).
-
The Inversion_Sbox.txt is checked at each start and if it's corrupted (not here or wrong), the program will generate one before starting.
-
Any generator for El-Gamal is designed to resist common attacks and it's found via the principle of Schnorr's group. More information by reading the code about El-Gamal here.
-
The generation of safe prime numbers is done by optimizing the search. We start from p prime number and check if 2p+1 is also prime OR if (p-1)/2 is also prime. The source code dedicated to this subject has been commented in order to understand the thinking process.
-
The difficulty of the proof of work established is adjusted according to the size of the blocks using a power function approximated by induction (i.e. by experimentation).
-
The blockchain simulation is single-threaded, so adding miners will not speed up block validation. As we can directly influe on on the block validation difficulty this is not problematic for the simulation understanding.
-
The simulation uses the UTXO system which is for example used in Bitcoin.
-
For RSA or ElGamal encryption/decryption, if the message is longer than our current modulus, it causes problem to process (i.e. Mathematically outside the modulus). To overcome this, we use a reversible mapping function : If the input message is larger (after conversion in integer) than the module of our encryption algorithm, we divide said message into several parts strictly smaller than the size of the module (i.e. With a 128-bit key, a 488-bit message is divided into 120-bit sub-messages).
-
Base64 is used instead of hexadecimal for storing and displaying encrypted keys and/or messages. Base64 takes 4 characters for every 3 bytes, so it's more efficient than hex.
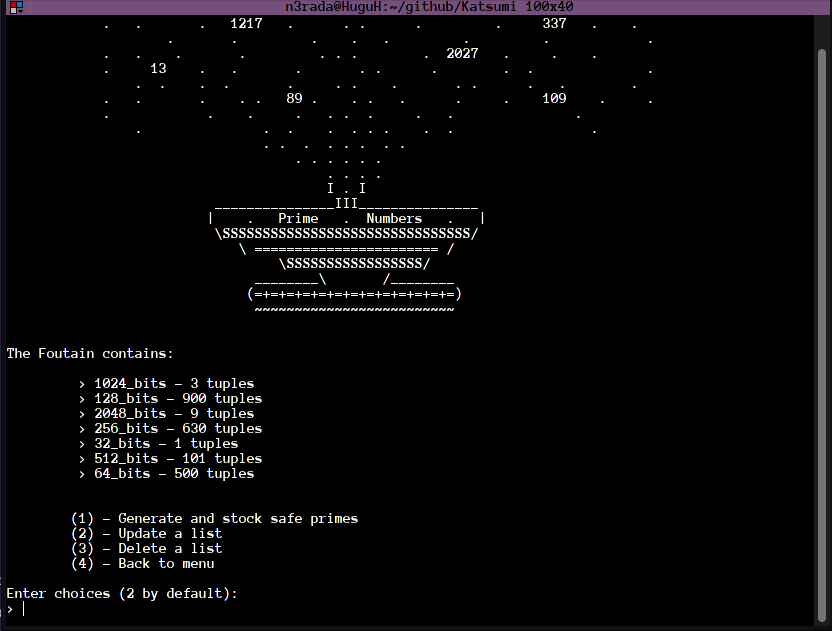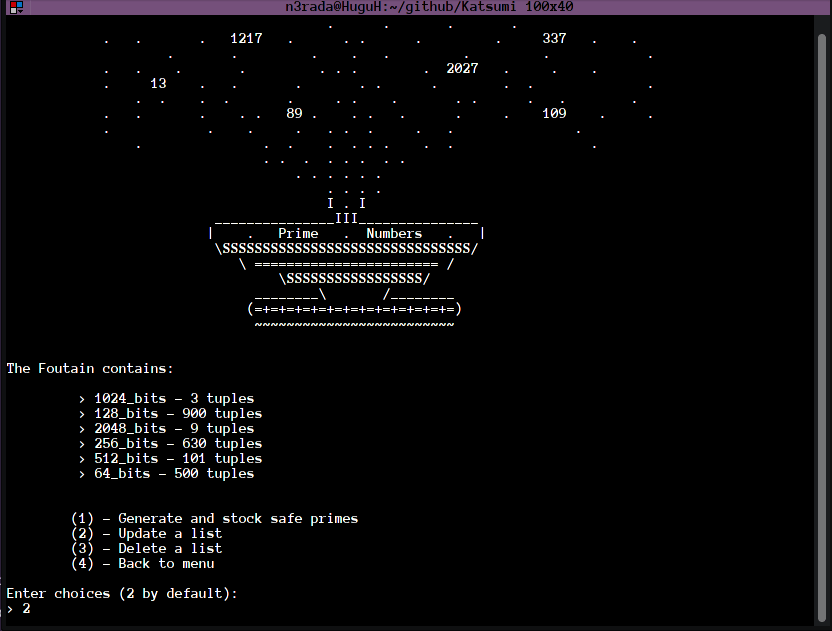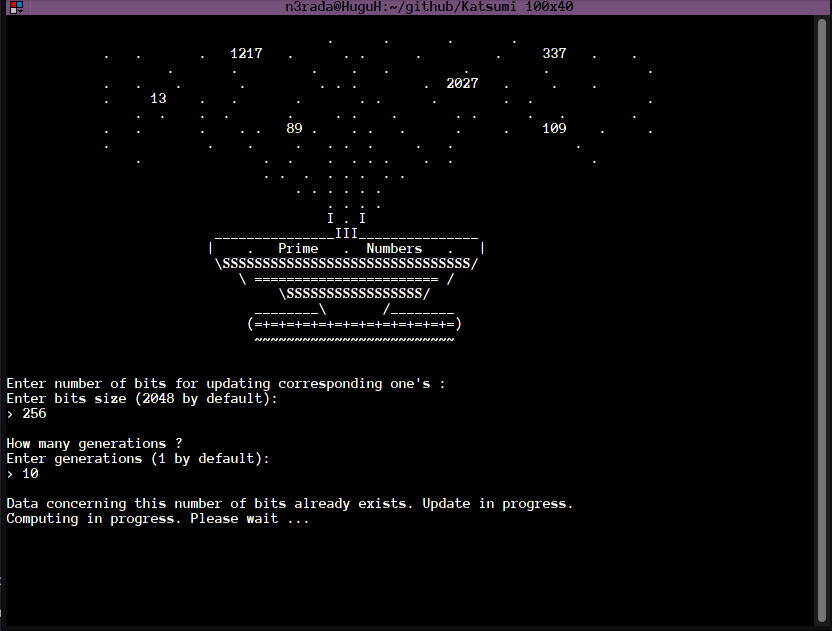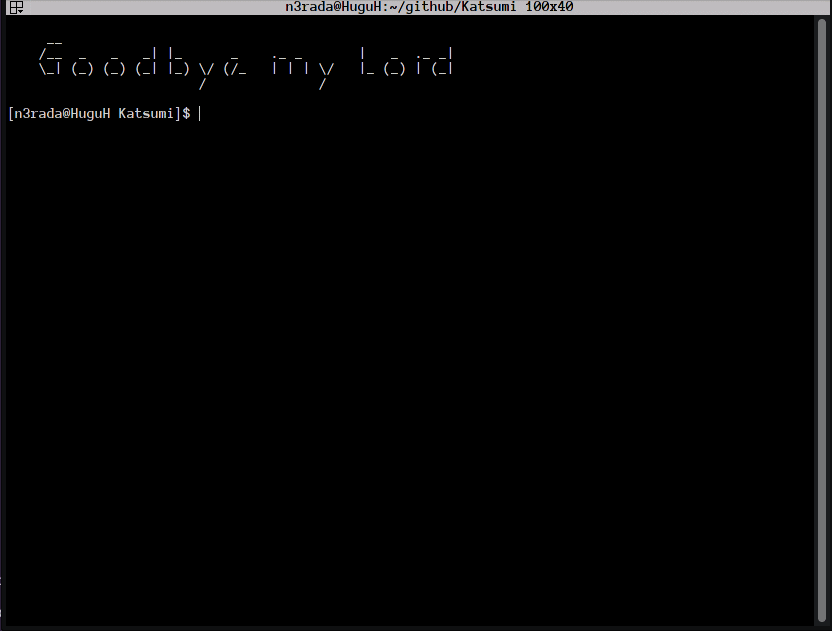
Generating safe primes can take a lot of computing time. To overcome this problem, we have imagined storing our safe primes in an accessible and editable location. We decided to call this thing: The Prime Numbers Fountain's
With this method, the user can have safe prime numbers loaded in his free time and use them appropriately at the right time.
Python natively uses only one core. So we have multiprocessed the safe prime number search using 85% of the core capacity.
Each measurement is based on a i7-10510U with 2.5GHz.
- The generation of the inverses in a binary Galois field (Z2) of degree 16 takes about 117 secondes (average over 5 trials).
- Generating a safe prime of 512 bits take at average 12.4 secondes for 10 tests.
- Generating a safe prime of 2048 bits take at average 71 minutes for 4 tests.
-
An obvious improvement would be to integrate the elliptic curves. This is a notion that came up at the end of the semester and which, respecting the deadline, could not be implemented (and was not required).
-
Using Schnorr signatures for our BlockChain.
-
Group RSA and ElGamal into a parent class to benefit from function heritage (i.e. use object-oriented programming).
Katsumi is licensed under the terms of the MIT Licence and is available for free - see the LICENSE.md file for details.
Here is some useful links for documentation concerning related subjects:
- https://en.wikipedia.org/wiki/Quadratic_residue
- https://en.wikipedia.org/wiki/Cryptographically_secure_pseudorandom_number_generator
- https://andersbrownworth.com/blockchain/
- https://www.random.org/analysis/
- https://en.wikipedia.org/wiki/Hamming_weight
- https://www.keylength.com/ - for choosing appropriated key length's.
- https://blkcipher.pl/assets/pdfs/gcm-spec.pdf - for GCM implementation
To the attention of the GS15 students who will be passing by, say hi to Rémi, then ask him if your project is better than ours. If it is, we owe you a beer, but don't kid yourself, your project won't be better. Good luck! 😉