Nobo (or noisy-bayesian-optimization)

Nobo is a library for optimizing very noisy functions using bayesian optimization. In particular functions p(x) -> [0,1] for which you only observe a random variable V_x ~ Bernoulli(p(x)). This might model A/B testing or a game playing program.

The following example shows how to use Nobo to find the minimum of p(x) = x^2 over [-1, 1] in this situation:

>>> import nobo, skopt, random
>>>
>>> def f(x):
>>>     return int(random.random() < x[0]**2)
>>>
>>> bo = nobo.Optimizer([skopt.utils.Real(-1, 1)])
>>> for j in range(50):
>>>     x = bo.ask(verbose=True)
>>>     bo.tell(x, f(x))
>>>
>>> x, lo, y, hi = bo.get_best()
>>> print(f'Best: {x}, f(x) = {y:.3} +/- {(hi-lo)/2:.3}')
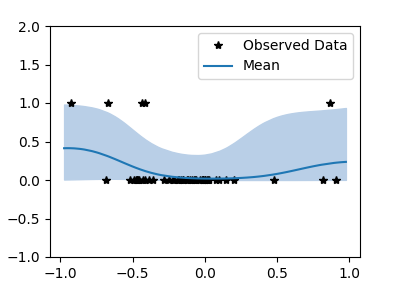
>>> bo.plot()
...
Best: [0.05464264314195355], f(x) = 0.018 +/- 0.0213

Implementation

Nobo uses gpytorch to do Gaussian Process Regression. This has the advantage over the classic sciki-optimize GaussianProcessRegressor that we can specify a non gaussian likelihood such as, in our case, Bernoulli.

The acquisition function used is Lower Confidnce Bound, taking as the next x to investigate the argmin_x mean(x) - log(n)*stddev(x) where n is the number of points already considered.

Chess Tuner

A classic use of Black Box Noisy Optimization is training the hyperparameters of game playing programs. In chess/chess_tuner.py we include a useful tool giving a complete playing and optimization pipeline. An example of usage is:

$ python python -m chess_tuner.chess_tuner sunfish -n 1000 -movetime 40 -conrrency=20
        -book lines.pgn -games-file tune_out.pgn
        -opt eval_roughness 1 30 -opt qs_limit 1 400
        -log-file tune.log -debug tune_debugfile -conf engines.json -result-interval 10
Loaded book with 173 positions
Loading 20 engines
Parsing options
Reading tune.log
Using [26.0, 72.0] => 0.0 from log-file
Using [23.0, 72.0] => 0.0 from log-file
Using [26.0, 140.0] => 0.0 from log-file
Using [21.0, 175.0] => 1.0 from log-file
...
Starting 2 games 113/1000 with {'eval_roughness': 5, 'qs_limit': 79}
Starting 2 games 114/1000 with {'eval_roughness': 11, 'qs_limit': 115}
Starting 2 games 115/1000 with {'eval_roughness': 27, 'qs_limit': 167}
Starting 2 games 116/1000 with {'eval_roughness': 18, 'qs_limit': 176}
Starting 2 games 117/1000 with {'eval_roughness': 13, 'qs_limit': 113}
Starting 2 games 118/1000 with {'eval_roughness': 16, 'qs_limit': 17}
...
Finished game 115 [27, 167] => 1.0 (1-0, 0-1)
Starting 2 games 133/1000 with {'eval_roughness': 6, 'qs_limit': 194}
Finished game 130 [16, 174] => 1.0 (1-0, 0-1)
Starting 2 games 134/1000 with {'eval_roughness': 19, 'qs_limit': 176}
Summarizing best values
Best expectation (κ=0.0): [7, 78] = 0.363 ± 0.424 (ELO-diff 132.3 ± 164.0)
...

Here two (uci or xboard) parameters eval_roughness and qs_limit are optimized. Games are played against the unoptimized engine. For all available options see python -m chess_tuner.chess_tuner --help. The code is a fork of the fastchess chess tuner, which used normal gaussian bayesian optimization, and thus would often converge to the wrong values.

Installation

You need to pip install numpy scipy scikit-optimize gpytorch torch matplotlib. To run the chess tuner you also need pip install chess. You can then git clone git@github.com:thomasahle/noisy-bayesian-optimization.git and run python noisy-bayesian-optimization/chess/chess_tuner.py directly.