Hyperoperators

hyperop is a small library for representing really, really, ridiculously large numbers in pure python. It does so using hyperoperations.

Hyperoperation 0, H0 is the successor function, H0(None, 4) = 5
H1 is addition, H1(2,4) = 2 + (1+1+1+1) = 6
H2 is multiplication (repeated addition), H2(2,4) = 2+2+2+2 = 8
H3 is exponentiation (repeated multiplication), H3(2,4) = 2*2*2*2 = 16
H4 is tetration (repeated exponentiation) H4(2,4) = 2^(2^(2^(2))) = 65536
...
Hyperoperation n is repeated Hyperoperation (n-1)

Fundamentally, hyperop works recursively by applying a fold-right operation:

H[n](x,y) = reduce(lambda x,y: H[n-1](y,x), [a,]*b)

Installation

pip install hyperop

To install the latest version use:

pip install git+https://github.com/thoppe/python-hyperoperators

Examples

from hyperop import hyperop

H1 = hyperop(1)
print(H1(2,3), H1(3,2), H1(5,4))
# >> 5, 5, 9

H3 = hyperop(3)
print(H3(2,3), H3(3,2), H3(5,4))
# >> 8, 9, 625

from math import log
H = hyperop(4)
print(H(2,5))
>>> 200352993040684646497....45587895905719156736

print(log(log(log(log(H(2,5),2.0),2.0),2.0),2.0) == 2)
>>> True

Approximate infinite tetration. Show that sqrt(2)^sqrt(2)^... where the tower continues an infinite amount of times is 2.

H4 = hyperop(4)
print(H4(2**0.5, 200))
# >> 2.0

Calculate the incomprehensibly large, but finite Graham's number:

def GrahamsNumber():
    # This may take awhile...
    g = 4
    for n in range(1,64+1):
        g = hyperop(g+2)(3,3)
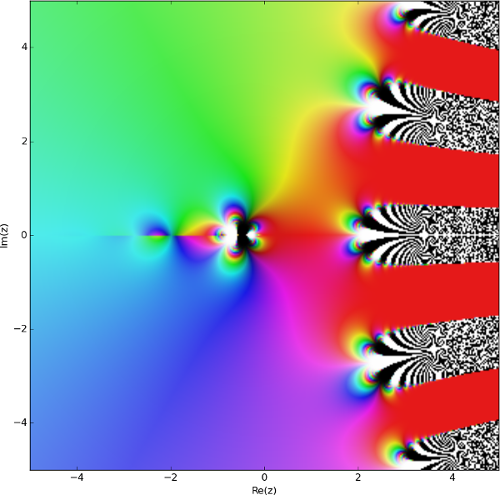
    return g

Plot the phase angle on the complex plane over tetrating four times H4(z,4)

from hyperop import hyperop
import mpmath

H = hyperop(4)
f = lambda z: H(z,4)
mpmath.cplot(f, verbose=True, points=100000)

Bounded hyperoperators

Sometimes, especially in the case of small complex numbers, you only care about numbers that stay bounded during the calculation. That is, you'd only like to keep the result for some bound z such that H[n](a,b) <= z. The class bounded_hyperop does just that:

from hyperop import bounded_hyperop
Hb = bounded_hyperop(4, bound=1000)
print(Hb(2,3), Hb(2,4))
# >> 16 inf

Caveats

Higher order hyperoperations (from tetration and above) are not associative, thus tetration H4(2,4) = 2^(2^(2^(2))) = 65536 is not H4(2,4) != 2^(2*2*2) = 256.

Since tetration is not defined for non-integral heights, the second argument of tetration and both arguments of pentation and above are restricted to non-negative integer values.

Talks & Press

Hyperop was featured in issue #231 of Python Weekly!

This library was first presented at DC's Hack && Tell (Feb. 2016). Talk link.

License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.