Projeto desenvolvido no âmbito da unidade curricular PLOG.
- Tiago Duarte da Silva - up201806516 - Turma 3
- Ricardo Jorge Cruz Fontão - up201806317 - Turma 3
Instalar e correr o SICStus prolog, caso esteja a ser usado o terminal dedicado em windows, aconselhamos a ir a Settings > Font e trocar para uma font monospaced (por exemplo Consolas).
Para correr o jogo em si, corra (re)consult('game.pl') e corra a função play sem argumentos.
- Regras de jogo
- Representação interna do estado de jogo
- Visualização do estado de jogo (intercalar)
- Screenshots
- Lógica de jogo
- Representação do estado de jogo
- Visualização de estado do jogo
- Estrutura de um move
- Lista de jogadas válidas
- Execução de jogadas
- Final de jogo
- Avaliação do tabuleiro
- Jogada do computador
- Loop de Jogo
- Conclusões
- Bibliografia
Chegar com as 3 bolas ao canto do jogador adversário.
- Tabuleiro de 5x5
- 3 bolas para cada jogador
- 8 anéis para cada jogador
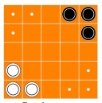
Cada jogador começa por colocar 3 anéis no seu canto e 1 bola em cima de cada anel conforme a imagem.
- Quando um componente entra em jogo, não pode voltar a sair.
- Uma bola pode apenas ser colocada em cima de um anel da mesma cor.
- Adjacente pode ser ortogonalmente ou diagonalmente.
- Quando uma bola chega a um dos espaços finais não pode voltar a sair.
Um turno consiste em dois passos:
- Colocar no tabuleiro ou mexer um dos próprios anéis
- Mexer uma das próprias bolas
Se não for possível uma jogada, o jogador perde automaticamente. No caso de existirem 3 bolas de qualquer cor nos home spaces de um jogador no final do seu turno, ele perderá o jogo.
Nesta fase podemos colocar um anel de fora do tabuleiro ou recolocar um que esteja já em jogo. Só podem ser movidos anéis que estejam expostos (não tenham qualquer bola ou anel por cima). O lugar onde se coloca o anel jogado pode ser qualquer um que não tenha uma bola em cima. Se tiver anéis nessa casa coloca-se por cima deles.
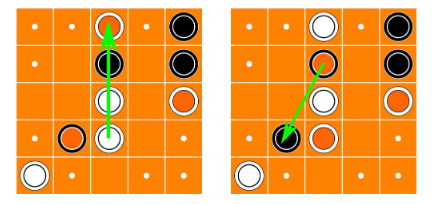
A primeira possibilidade é mexer a nossa bola para uma casa adjacente que tenha um anel nosso exposto em cima.
A segunda opção é "passar" por cima, em linha reta, de quantas bolas adjacentes houver, tendo que aterrar num anel exposto do próprio jogador. De seguida o jogar tem de recolocar qualquer bola que passou por cima que pertença a um adversário para uma posição válida(anel da mesma cor). Se alguma das bolas não poder ser recolocada o salto não pode ser feito.
Se no fim do turno do jogador todas as suas bolas estiverem no canto oposto do início do jogo, esse jogador ganha.
A representação interna do jogo (GameState) consiste de uma lista de 4 elementos:
- O primeiro elemento é uma lista de listas de stacks (listas) em que cada stack representa uma célula do jogo e armazena as peças lá colocadas preservando a sua ordem (ordem crescente de índice corresponde a ordem crescente de altura).
- O segundo elemento é o número de anéis brancos que não estão em jogo.
- O terceiro elemento é o número de anéis pretos que não estão em jogo.
- O quarto elemento representa a quantidade de peças que são representadas de cada célula, de forma a que o jogo fique "legível".
Relativamente a cada peça usamos uma representação númerica diferente, por exemplo, um anel branco pode ser representado pelo número inteiro 1 e um anel preto pelo número inteiro 2.
No caso de uma célula estar vazia a lista que a representa também é vazia.
Representações do estado inicial e de um possível estado intermédio e final:
% 1 : White Ring
% 2 : Black Ring
% 3 : White Ball
% 4 : Black Ball
initial(GameState) :-
GameState = [
[ % Game board
[ [], [], [], [2, 4], [2, 4]],
[ [], [], [], [], [2, 4]],
[ [], [], [], [], []],
[ [1, 3], [], [], [], []],
[ [1, 3], [1, 3], [], [], []]
],
5, % Unplayed white rings
5, % Unplayed black rings
3 % Shown Stack Size
].
mid_game(GameState) :-
GameState = [
[ % Game board
[ [], [], [], [2, 1], [1, 3]],
[ [], [1, 3], [], [2, 4], [2, 4]],
[ [], [1], [2, 1, 3], [2], [1]],
[ [2, 4], [2, 1], [2], [], []],
[ [], [], [], [], []]
],
1, % Unplayed white rings
0, % Unplayed black rings
4 % Shown Stack Size
].
end_game(GameState) :-
GameState = [
[ % Game board
[ [], [], [], [1, 2, 1, 3], [1, 3]],
[ [], [], [], [2, 4], [2, 1, 3]],
[ [], [1], [2, 1], [], []],
[ [2, 4], [2, 1], [2, 1], [], []],
[ [2, 4], [], [], [], []]
],
0, % Unplayed white rings
0, % Unplayed black rings
5 % Shown Stack Size
].A informação relativa a que jogador joga a seguir é guardada em Player:
- 0 -> Branco
- 1 -> Preto
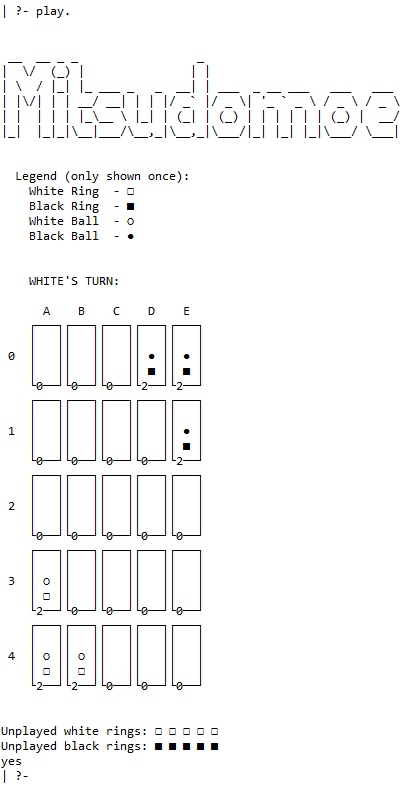
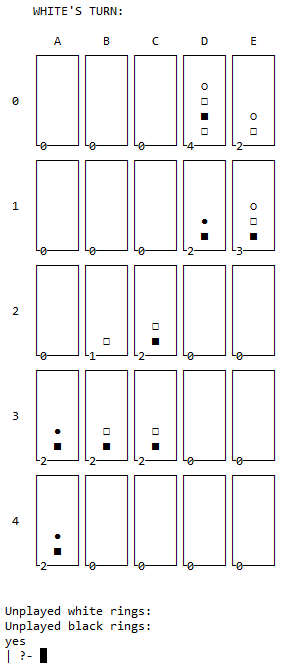
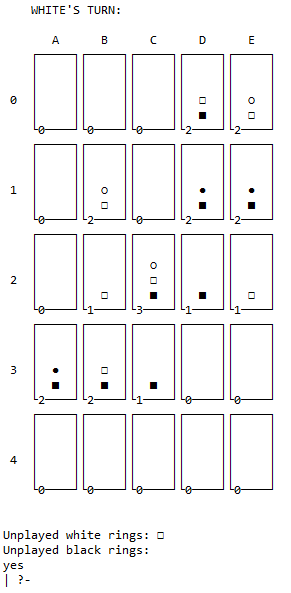
O predicado display_game\2 desenha no ecrã um tabuleiro de qualquer dimensão até 27x27. Para cada linha do tabuleiro é chamado o predicado print_line\4, que é divido em top, mid e bot, desenha as linhas necessárias na consola. Cada célula pode ser identificada por um par número e letra, inspirado pelo sistema do xadrez.
No canto inferior esquerdo de cada célula é ainda mostrado o número total de peças na stack respetiva. Este número pode ser alterado ao longo do jogo e define ainda o tamanho de cada célula (em altura e largura) para o tabuleiro ser sempre de visualização fácil. A largura de cada célula é sempre um número ímpar para garantir que o espaçamento entre os vários elementos é correto.
O predicado print_line_mid\4 é responsável por desenhar as N peças no topo da stack, mas sempre encostadas à base da frame da célula. Para este efeito, o predicado get_stuffed_elem_from_end0\s dá-nos qual o código da peça numa dada posição da stack, mas como que se estivesse stuffed (por exemplo: [1, 2] seria interpretado como [1, 2, 0] para a visualização permanecer correta, mas sem nunca alterar a lista).
Pode ser encontrado aqui.
A visualização do jogo não foi alterada desde o relatório intercalar, portanto pode ser visto aqui, De acordo com o feedback do docente, as células foram expandidas horizontalmente para o tabuleiro ficar menos esticado.
Os menus introduzidos para a seleção de jogadas, os níveis da AI e a seleção do modo de jogo, podem ser encontrados no ficheiro input.pl. Caso seja introduzido um input inválido, a linha inteira será ignorada.
Para a leitura do modo de jogo usamos o predicado read_mode/1, que mostra a mensagem com as opções possíveis e depois lê a opção do utilizador.
Para a leitura da dificuldade da AI, lemos a dificuldade (random ou smart) para a AI uma vez se o modo for Humano vs AI ou duas vezes se o modo for AI vs AI.
Para a leitura de cada jogada e de acordo com a sua estrutura, começamos por perguntar ao utilizador se pretende colocar um anel novo ou mover um que já esteja no tabuleiro, perguntando sempre as coordenadas. De seguida as coordenadas da bola que deseja mover e as coordenadas do destino.
Caso seja necessário dar vault por cima de bolas inimigas, será necessário o utilizador introduzir como as mover. Caso seja necessário mover mais que uma é mostrado as opções e o utilizador escolhe. Caso haja apenas uma bola para deslocar, o programa assume logo qual é e apenas pede ao utilizador o seu destino.
Toda a introdução de coordenadas pode ser feita na forma de "A3" ou "3A", ou seja, coluna e linha ou vice-versa, com as letras maiúsculas ou minúsculas. Os inputs também não necessitam de um ponto final no fim e são resilientes ao ponto de ser extremamente difícil terminar a sua execução por engano.
De forma a representar cada move é usado uma lista de listas, para facilitar eventuais alterações futuras:
As coordenadas são sempre representadas em [Row, Col] e um displace é [Coordenadas Iniciais, Coordenadas Finais].
Move -> [DisplaceRing, DisplaceBall, [Displaces], Player]
DisplaceRing -> Displace do anel a mexer (Coordenadas iniciais são [-1,-1] se a jogada for colocar um anel novo em jogo)
DisplaceBall -> Displace da bola a mexer
[Displaces] -> Displaces às bolas inimigas se ocorrer um vault sobre elas (vazia caso contrário)
Player -> Jogador que realiza a jogada (white/black)
A geração de jogadas válidas está implementada usando o predicado get_valid_move/3, que gera uma jogada possível. O predicado valid_moves/3 apenas contém um findall/3 de get_valid_move/3.
A geração de uma jogada está dividida em 3 partes:
- Se o jogador tiver anéis por colocar, pôr um anel em qualquer casa sem uma bola no topo. Para cada anel exposto, movê-lo para qualquer casa sem uma bola no topo.
- Simular a fase de mover o anel, para garantir que a informação que mais tarde necessitamos é correta.
- Para cada bola do jogador tentar movê-la para cada casa que tenha um anel exposto.
- Caso tenhamos dado vault por cima de bolas inimigas realocá-las.
Para gerar cada parte (ex: escolher uma bola ou uma casa para colocar o anél) é usado o predicado get_stack_if/3 que recebe um predicado e todos os seus argumentos (à exceção do último) e devolve a posição da primeira stack do tabuleiro para a qual o predicado é verdade. Com backtracking irá percorrer o tabuleiro inteiro e gerar todas as coordenadas onde o predicado é verdadeiro.
Caso haja bolas inimigas para mover, o processo é um pouco diferente:
-
O predicado get_enemy_relocation/4 gera uma e uma só vez cada outcome possível. Um outcome é definido como o resultado final, isto é, onde ficam as bolas inimigas no final da jogada.
-
Cada outcome é tratado como um conjunto de posições e é gerado através das combinações de todas as posições possíveis, as bolas a mover e os anéis inimigos expostos, excetuando o conjunto completo das bolas a mover. Esta operação é efetuada no predicado get_outcome/3.
Para garantir que geramos todas as possibilidades corretas, é necessário ter em atenção que é possível deslocar as bolas das posições {A, B, C} para {D, A, B}. Como a ordem de mover as bolas ser arbitrária, podemos mover A para D, depois B para onde estava A e finalmente C para onde estava B.
Assim sabemos que no pior caso teremos
8C3 - 1 = 56outcomes. 8 posições possíveis excetuando o caso em que as bolas ficam todas nas suas posições antigas, pois é impossível. -
Dado um outcome qualquer e as bolas que é necessário mover conseguimos inferir pelo menos uma ordem de movimentos que leva ao outcome. O predicado get_relocations_from_outcome/3.
Esta operação pode ser descrita de seguinte forma: Seja 'B' o conjunto de bolas a mover e 'O' o conjunto de posições do outcome:
- P é o conjunto de posições das bolas com prioridade a mover, isto é, bolas que já estejam numa das posições do outcome, pois têm que ser movidas primeiro
- R é o conjunto de posições das bolas sem prioridade
- F é o conjunto de posições das posições livres para mover a bola
P = B ∩ O R = B \ P F = P \ P- Movemos todas as bolas prioritárias para uma das posições livres e adicionamos a posição original de cada ao conjunto de posições livres.
- Movemos as restantes bolas para as restantes posições livres, adicionando a posição original de cada ao conjunto de posições livres.
- Juntar as duas listas de deslocamentos para obter as recolocações ordenadas de forma válida
Graças à logica descrita acima, geramos todas as jogadas possíveis que levam a um resultado diferente uma e uma só vez.
O nosso predicado move/3 está divido em 3 partes.
Numa primeira parte fazemos uma chamada ao predicado new_move/5 que decompõe um move nas suas partes (DisplaceRing, DisplaceBall, Displaces, Player).
De seguida, temos a fase de movimento do anel em que usamos o predicado move_ring_phase/4. Este predicado por sua vez chama o predicado place_new_ring/4 ou move_ring/4 dependendo se queremos mexer um anel já em jogo ou colocar um novo.
Por fim usamos o predicado move_ball_phase/5 que move tanto a bola especificada no move como os possíveis Displaces gerados por algum vault. Este predicado funciona usando os predicados move_ball/5 que move uma bola e retorna os Displaces a fazer se for um vault e relocate_balls/5 para tratar de quaisquer bolas que possam ter de ser realocadas por causa de um vault (indicadas pelo predicado anterior).
Para verificarmos o final de jogo usamos o predicado game_over/3.
A primeira condição verificada é se as casas do inimigo ficaram ocupadas todas com bolas do jogador, com recurso ao predicado check_enemy_cells/2. Neste caso o jogador que executou a jogada ganha.
De seguida, verificamos se as casas iniciais do jogador que executou a jogada estão ocupadas com bolas de qualquer cor (no final da sua própria jogada). Esta verificação é feita para prevenir jogo passivo. Neste caso o inimigo ganha.
Por fim, verificamos se o oponente ficou sem jogadas (por exemplo se não tiver mais anéis para colocar em jogo e nenhum dos seus está exposto). Para verificar este caso fazemos uma chamada a get_valid_move/3 com o inimigo e caso ela falhe o autor da jogada é declarado como vencedor. Será de relembrar que o predicado mencionado acima gera apenas uma jogada válida (se possível), portanto é bastante mais eficiente do que verificar se a lista de jogadas válidas é vazia.
Se nenhum dos casos anteriores se verificar, o predicado unifica Winner com none.
A seguir ao predicado game_loop/3 é usado o predicado handle_winner/5 que, baseado no vencedor, mostra a mensagem de vitória ou faz a chamada 'recursiva' do predicado game_loop/4 se este não existir.
Para que a AI desenvolvida possa escolher o melhor move num certo momento foi criado o predicado value/4, que retorna o valor para de um dado GameState.
Em primeiro lugar, é verificado se existem 3 bolas de qualquer cor nas nossas posições iniciais do jogador. Neste caso a AI iria "suicidar-se", logo damos a esta jogada um valor muito alto, que é avaliado como sendo uma jogada extremamente má.
De seguida se as casas do inimigo contiverem as 3 bolas do jogador. Se isto acontecer estamos perante uma jogada vencedora, logo damos-lhe um valor negativo de valor absoluto muito alto de forma a que esta jogada seja escolhida de certeza.
Se nenhuma das condições anteriores se aplicar passamos à verificação normal das jogadas.
O valor de um tabuleiro consiste em calcular a soma das médias da distância de cada bola a cada célula do oponente (objetivo). Quanto menor for este valor melhor é considerada a jogada.
Valor do Tabuleiro = Média(dist(B1, C1), dist(B1, C2), dist(B1,C3)) + Média(dist(B2, C1), dist(B2, C2), dist(B2,C3)) + Média(dist(B3, C1), dist(B3, C2), dist(B3,C3))
B -> Bola
C -> Casa final do oponente
A AI implementada tem duas dificuldades: smart e random.
Na dificuldade random, o predicado choose_move/4 usa o predicado valid_move/3 e depois escolhe um membro aleatório do ListOfMoves.
Para impedir que a AI se 'suicidasse' consistentemente durante os primeiros 10 turnos, foi implementada uma verificação extra usando random_select que vai extraíndo aleatóriamente uma jogada válida e no caso de levar a um 'suicídio' continua a extração. Caso se esgotem as jogadas possíveis admite derrota e usa random_member/2 para escolher uma derrota sobre a lista original.
Na dificuldade smart o predicado choose_move/4 usa o predicado valid_move/3 para gerar ListOfMoves com todos os moves possíveis. De seguida usamos um predicado criado por nós chamado min_map/3 que retorna o elemento de uma lista para o qual o valor de um predicado é mínimo, neste caso, a jogada ótima.
O predicado auxiliar passado ao min_map/3 é lambda_evaluate_move/4, que simula e calcula o valor de um move. Atualmente a decisão da melhor jogada é bastante rápida, mas é usado um sleep(1) para permitir visualizar melhor as jogadas da AI.
Para determinar o valor de um move fazemos uso do predicado value/4. No entanto, em vez de apenas calcularmos o valor do GameState após um move para nós, também calculamos qual o seu valor para o inimigo de forma a tentar maximizar o valor para nós e minimizar o valor para o adversário. A fórmula usada é a seguinte:
Valor de um Move = Valor para o Jogador + Valor para o Oponente * 0.5
De forma a que a AI não fique determinista e se torne um pouco mais interessante, a este valor ainda adicionamos um valor aleatório, ou seja, a fórmula passa a ser:
Valor de um Move = Valor para o Jogador + Valor para o Oponente * 0.5 + random(-0.25, 0.25)
O nosso loop de jogo encontra-se num predicado chamado actual_game_state/4 que contém os seguinte passos:
- Mostrar o estado atual do jogo no ecrã.
- Chamada de pick_move para a escolha de jogada. Se for a AI a jogar a jogada é pedida a choose_move e se for um humana a jogada é pedida através read_move ao terminal do Sicstus.
- Caso seja humano, chamada de repeat tal que, caso o jogador dê input a uma jogada inválida, a possamos voltar a pedir.
- Depois é validada e efetuada essa jogada. Em caso de sucesso cria-se o GameState seguinte.
- Depois verificamos se a jogada efetuada acaba o jogo com recurso a game_over e a handle_winner.
- Caso não haja vencedor, handle_winner irá chamar o predicado game_loop que apenas tem como objetivo alternar quem é a jogar se for AI vs Humano ou trocar os níveis de dificuldade se for AI vs AI, de forma a usar a dificuldade e modo certo em actual_game_loop.
O objetivo deste projeto era desenvolver na linguagem Sicstus Prolog um jogo de tabuleiro que incluísse representação gráfica, suporte para modos de jogo como por exemplo AI vs Humano ou AI vs AI e ainda tanto uma AI simples como outra aleatória. Todos os objetivos foram concluídos com sucesso.
Relativamente a known issues pode referir-se que a fórmula de valorização de GameStates podia ser melhorada possivelmente para incluir diferentes estratégias, por exemplo, defender as próprias casas ou até bloquear rings do oponente.
Por fim, melhorias possíveis para o futuro seria a implementação de uma AI que calculasse o valor das suas jogadas com vários níveis de profundidade, ou seja, ver até mais do que uma jogada no futuro (embora envolva calcular um pelo menos 8 milhões de jogadas válidas). Outra possibilidade seria alterar a quantidade de elementos mostrados por stack no terminal, visto já estar previsto no código do estado de jogo e da visualização. Por fim poderíamos usar tabuleiros maiores do que 5x5 apesar destes não serem referidos nas intruções do jogo, visto que são suportados pela nossa implementação.
Este trabalho contribuiu significativamente para o nosso entendimento da linguagem Prolog e dos seus detalhes.