max-separation-as-inductive-bias: A Python repository from tkasarla

Introduction

This repository is the official implementation of the arxiv preprint Maximum Class Separation as Inductive Bias in One Matrix.

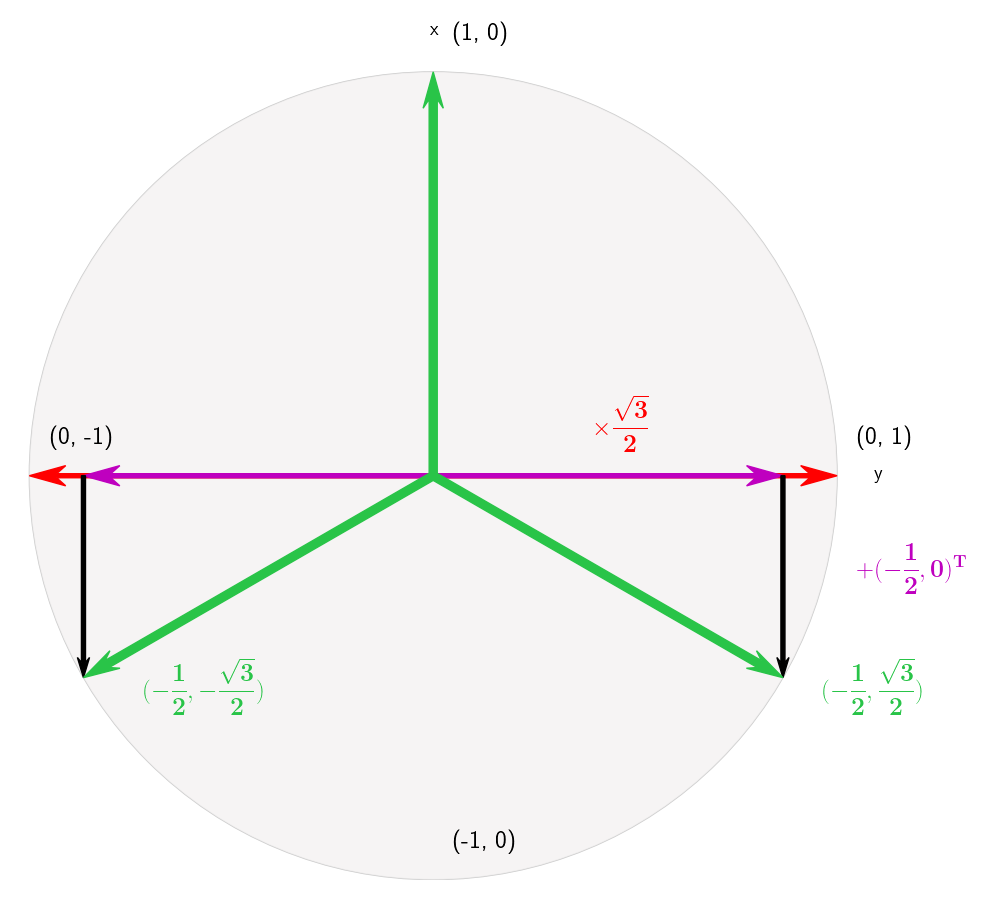
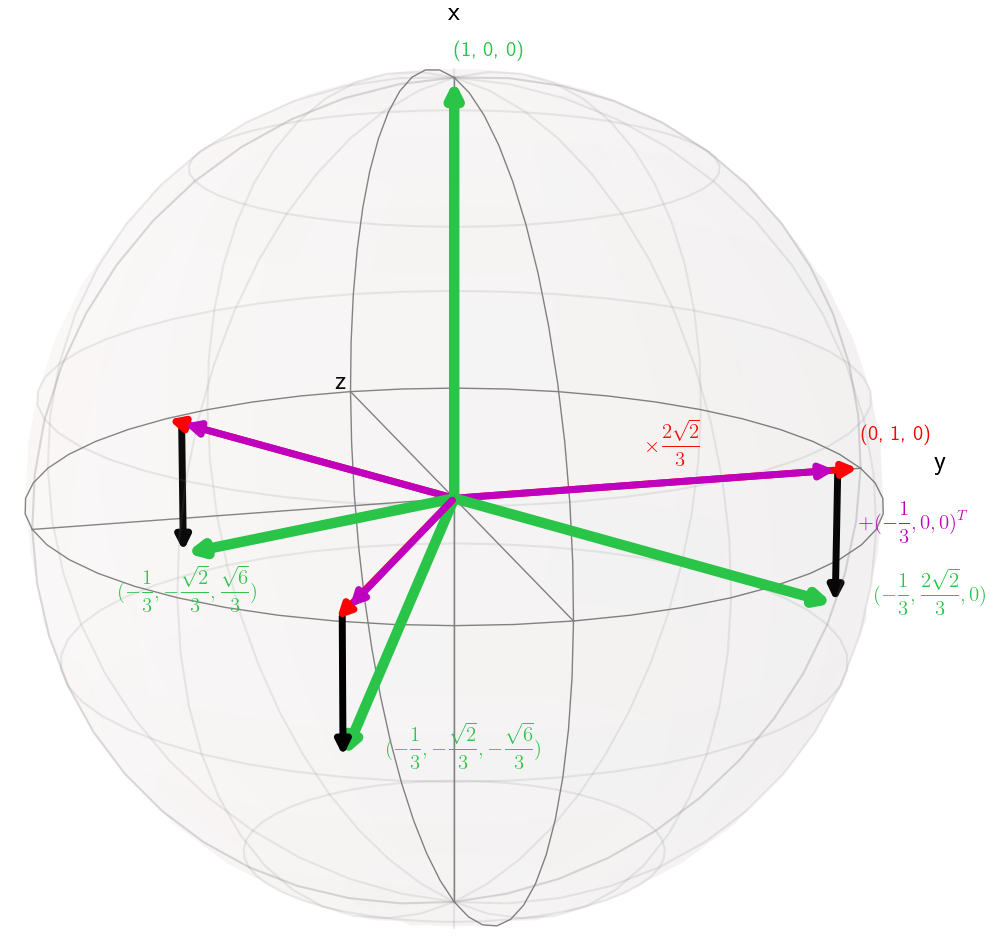
In our paper, we outline a closed form solution for separating $k+1$ class vectors on $k$ output dimensions. The proposed solution allows us to construct the matrix recursively.

The angle between any two class vectors is $-1/k$.

$$\begin{align} P_1&=\begin{pmatrix}1&-1\end{pmatrix} \in \mathbb R^{1\times2} \newline \newline P_k&=\begin{pmatrix}1&-\frac{1}{k}\mathbf1^T \newline \mathbf0&\sqrt{1-\frac1{k^2}} P_{k-1}\end{pmatrix} \in \mathbb R^{k\times(k+1)} \end{align}$$

Recursive update from 2 to 3 classes Recursive update from 3 to 4 classes

Requirements

To install requirements:

pip install -r requirements.txt

Create the Matrix with Maximum Class Separation

Generating the class vectors that are maximally separated from each other is the main contribution of our work.

Change the value of nr_classes in create_max_separated_matrix.py to match the total number of classes in your dataset.

Then to generate the matrix and save it to a numpy file, run:

python create_max_separated_matrix.py

After the npy file is saved, you can load it into your code (for examples check the training codes in LT_CIFAR folder). Alternatively, you can also load the matrix into code realtime by calling the function create_prototypes() in your code.

Results

For CIFAR-10, run create_max_separated_matrix.py and save prototypes-10.npy; for CIFAR-100, run and save prototypes-100.npy. For reproducing results of Table 1 in the paper, follow the README in LT_CIFAR.

TODO: update instructions on reproducing rest of the tables in the paper

Citation

Please consider citing this work using this BibTex entry

@article{kasarla2022maximum,
  title={Maximum Separation as Inductive Bias in One Matrix},
  author={Kasarla, Tejaswi and  and Burghouts, Gertjan J and van Spengler, Max and van der Pol, Elise and Cucchiara, Rita and Mettes, Pascal},
  journal={arXiv preprint arXiv:2206.08704},
  year={2022}
}