A tool for calculating necesaary tiles and unnecessary tiles for winning hands in Japanese mahjong.
- Necessary tiles:
- the tiles needed to win with least number of exchanges.
- decrease the shanten number when one of them is drawn.
- called "yuukouhai" or "ukeire" in Japanese.
- Unnecessary tiles:
- the tiles unneeded to win with least number of exchanges.
- keep the shanten number unchanged when one of them is discarded.
- called "yojouhai" in Japanese.
- Prepare a
std::vector<int>array representing a hand.
- The
nth element stores the number ofnth tiles.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| Manzu | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Pinzu | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Souzu | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Jihai | 27 (East) | 28 (South) | 29 (West) | 30 (North) | 31 (White) | 32 (Green) | 33 (Red) |
- For example, if you have manzu tiles (1, 2, 3), pinzu tiles (2, 4, 5, 7, 7, 9), and jihai tiles (East, West, White, White, White), define the following array.
std::vector<int> hand = {
1,1,1,0,0,0,0,0,0, //Manzu
0,1,0,1,1,0,2,0,1, //Pinzu
0,0,0,0,0,0,0,0,0, //Souzu
1,0,1,0,3,0,0 //Jihai
};- Calculate the shanten number, necessary tiles and the unnecessary tiles.
std::tuple<int,int,std::int64_t,std::int64_t> CalshtDW::operator()(const std::vector<int>& hand, int m, int mode)NOTE: Normally, substitute the value obtained by dividing the number of tiles by 3 into
m.
NOTE:
modespecifies for which winning pattern calculate shanten number. When the pattern is "General Form",modeis 1, when "Seven Pairs": 2, "Thirteen Orphans": 4. When calculating the Shanten number for multiple winning patterns, specify the logical sum of them.
NOTE: This method returns the value of shunten number + 1, mode, necessary tiles, unnecessary tiles. The mode indicates which winning pattern (General Form, Seven Pairs, Thirteen Orphans) has the minimum shunten number. Each valid/unnecessary tile is represented by a 64-bit integer. Whether 1 or 0 of the
i-th bit indicates whether thei-th tile is a necessary tile (or an unnecessary tile) or not.
For example, calculate the necessary tiles and unneccessary tiles of the hand defined above. It requires one of manzu tiles (1 to 9) or one of jihai tiles (East, West) for winning, however one of manzu tiles (2, 4, 5, 7, 9) or one of jihai tiles (East, West, White) is uneeded. The source code is as follows:
#include <iostream>
#include <bitset>
#include <vector>
#include "calsht_dw.hpp"
int main()
{
CalshtDW calsht;
// Set the location of shanten tables
calsht.initialize(".");
std::vector<int> hand = {
1,1,1,0,0,0,0,0,0,// manzu
0,1,0,1,1,0,2,0,1,// pinzu
0,0,0,0,0,0,0,0,0,// souzu
1,0,1,0,3,0,0// jihai
};
auto [sht, mode, disc, wait] = calsht(hand, 4, 7);
std::cout << sht << std::endl;
std::cout << mode << std::endl;
std::cout << std::bitset<34>(disc) << std::endl;
std::cout << std::bitset<34>(wait) << std::endl;
return 0;
}Output:
3
1
0010101000000000101011010000000000
0000101000000000111111111000000000
This program simultes single player mahjong. In each round, it discards one of unnecessary tiles, and then maximize the number of necessary tiles.
- Debug mode
$ mkdir build
$ cd build
$ cmake .. -DCMAKE_BUILD_TYPE=Debug
$ make
- Release mode
$ mkdir build
$ cd build
$ cmake .. -DCMAKE_BUILD_TYPE=Release
$ make
NOTE: A compiler compatiable with C++11 or higher is needed.
$ ./sample [number of rounds (e.g. 1000000)]
$ cat result.txt
Number of Tiles 14
Total 1000000
Time (msec.) 106499
Turn Shanten Number (-1 - 6) Hora Tempai Exp.
0 4 689 23224 194623 439207 285376 55254 1623 4e-06 0.000693 3.1576
1 36 3139 60055 312301 436206 169174 18856 233 3.6e-05 0.003175 2.76561
2 165 9550 118653 409619 368079 87961 5939 34 0.000165 0.009715 2.42371
3 575 22236 193284 461052 278799 42243 1805 6 0.000575 0.022811 2.12924
4 1585 43455 270484 467989 196448 19497 539 3 0.001585 0.04504 1.87492
5 3557 73558 341680 439988 132134 8916 167 0 0.003557 0.077115 1.651
6 7014 111731 397628 393033 86425 4115 54 0 0.007014 0.118745 1.45269
7 12342 155439 437312 337357 55610 1918 22 0 0.012342 0.167781 1.2743
8 19769 202505 460160 281105 35463 991 7 0 0.019769 0.222274 1.11299
9 29749 250970 466746 229544 22484 502 5 0 0.029749 0.280719 0.96557
10 42291 298561 460318 184296 14284 247 3 0 0.042291 0.340852 0.830474
11 57229 343412 444338 145635 9257 128 1 0 0.057229 0.400641 0.706667
12 74977 383949 420945 114180 5875 74 0 0 0.074977 0.458926 0.592249
13 94703 420040 392750 88629 3832 46 0 0 0.094703 0.514743 0.486985
14 116313 450680 362048 68448 2487 24 0 0 0.116313 0.566993 0.390188
15 140202 475546 330180 52435 1622 15 0 0 0.140202 0.615748 0.299774
16 165530 494708 298847 39820 1087 8 0 0 0.16553 0.660238 0.21625
17 192032 508775 268240 30169 780 4 0 0 0.192032 0.700807 0.138902
-
The first line shows the number of hand tiles, the second line shows the number of games, and the third line shows the execution time (milliseconds).
-
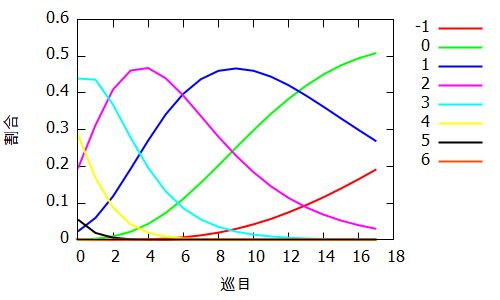
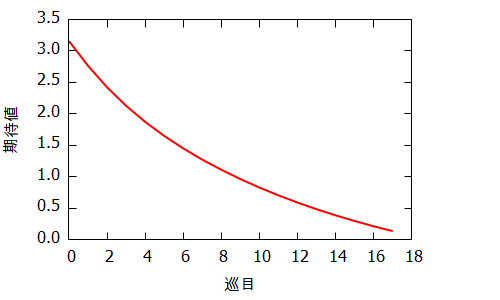
The sixth line onward shows the ratio of each shanten number (-1 to 6), winning ratios, tempai ratios, expected values of shanten numbers from left to right. The final line shows that the winning rate in single player mahjong is about 19%.
-
The graph belows shows the ratios and expected values of shanten number in each round.
Enable THREE_PLAYER.
Example:
$ cmake .. -DCMAKE_BUILD_TYPE=Release -DTHREE_PLAYER=on
Build tables of parameters required for calculating necesaary tiles and unnecessary tiles. Make "index_dw_h.txt" and "index_dw_s.txt".
$ ./mkind2.out
GNU General Public License v3.0.