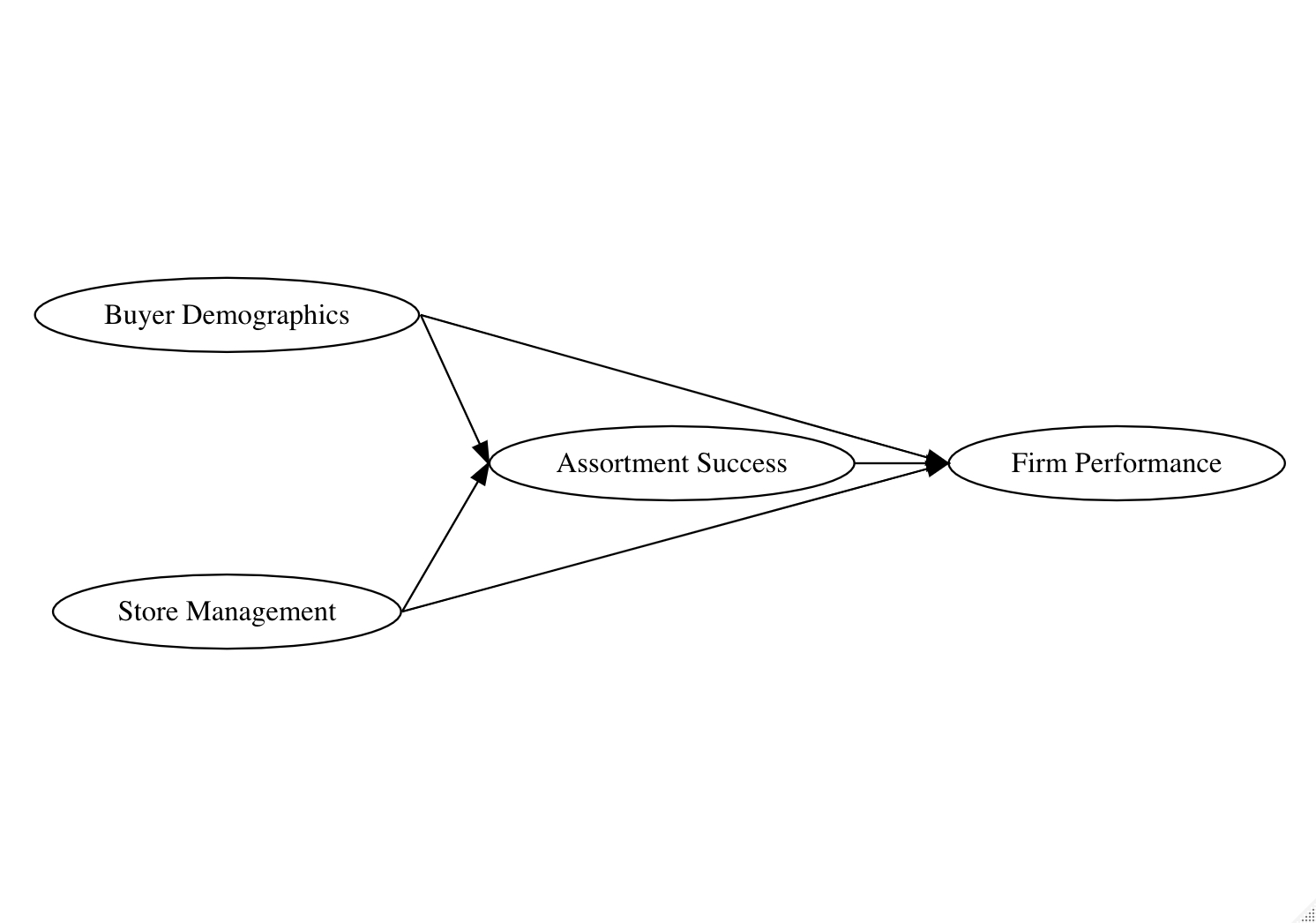
Most causal relationships in machine learning are direct, i.e. all the features predict with no causal relationship to each other. But what about more complicated causal relationships, such as this?
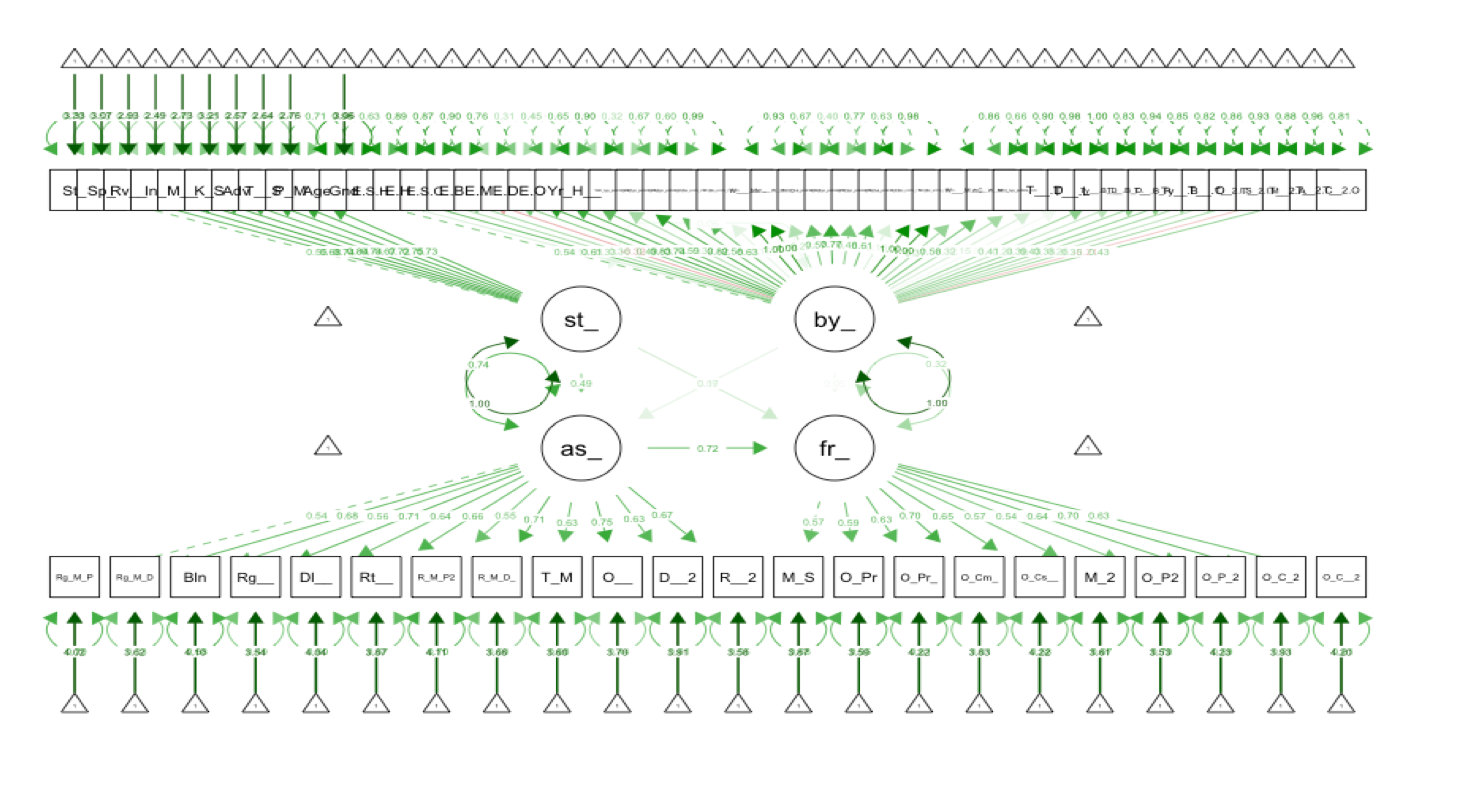
Structural equation modeling provides a means of estimating such relationships. In the example of my research, co-authored with Professors Youngjin Bahng and Doris Kincaid, the model from that diagram was estimated as an SEM model:
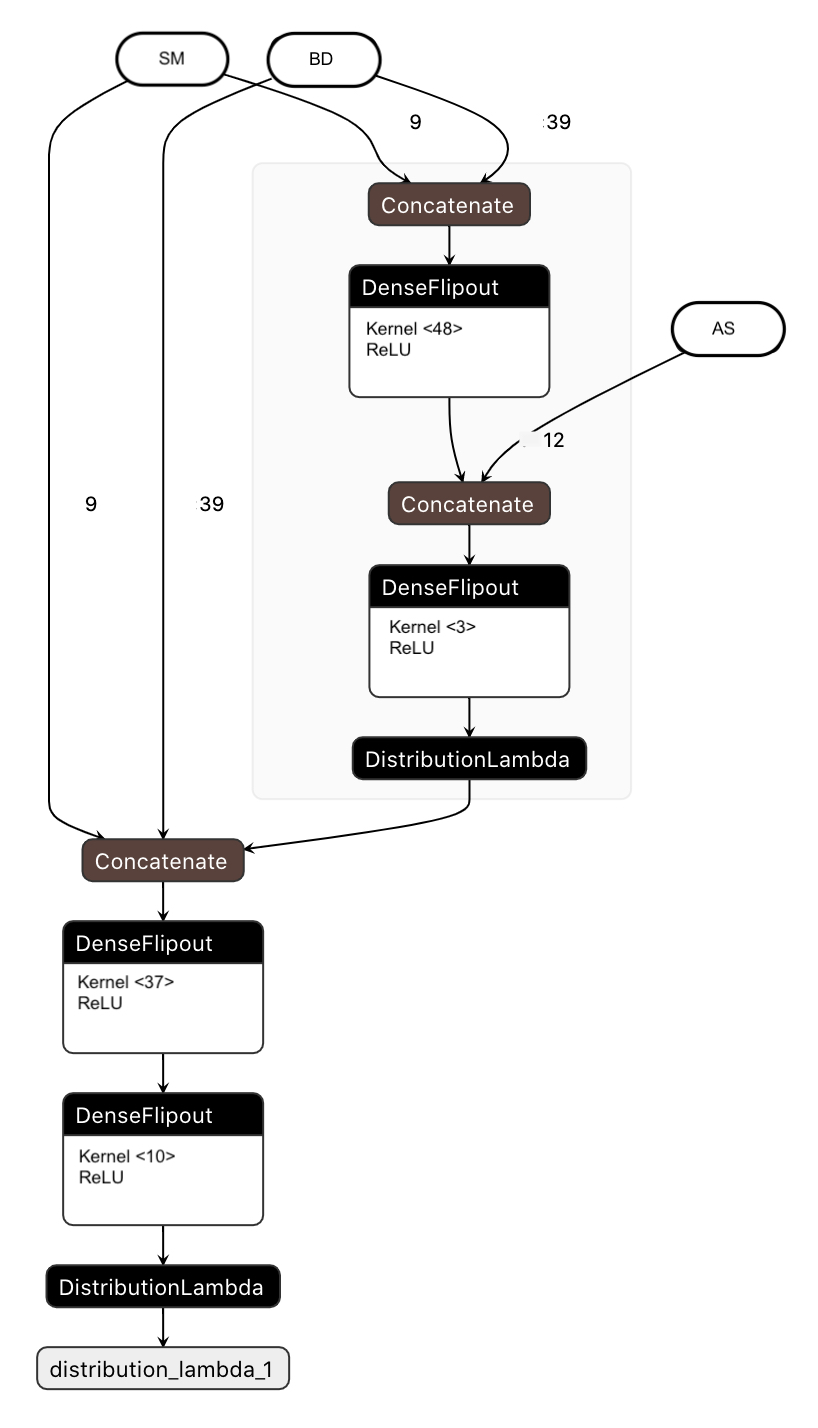
In my presentation at the 2021 ASA Symposium on Data Science and Statistics (full paper), I take that structural model and turn it into the following causal Bayesian neural network:
Why? Considering the intrinsic properties of the causal Bayesian neural network, the processing of tuning such a neural network can reveal much about the relationship between the features and firm performance. If hyperparameter tuning chooses neural network layer densities that are wider than the number of features in a particular node, then that indicates greater aleotoric uncertainty, and that prediction might improve with the addition of other features. In domains such as alternative data for investments and other areas of finance, that can indicate causal indicators that could use additional research.
Extrinsically, the neural network provides a prediction interval with upper and lower bounds that provides an estimate of the amount of uncertainty in prediction. This research shows that removing the SEM node with the weakest causal connection to firm performance speeds up the time to finding that estimate when uncertainty is added to the neural network using the Kullback-Leibler divergence. This opens up the possibility of estimating SEM in this manner after each epoch in a manner similar to Dropout in neural networks, though this depends on SEM path weights and applies to nodes/edges instead.
This code uses version 0.7.0 of Tensorflow-probability and Scikit-Learn to organize the experiments.