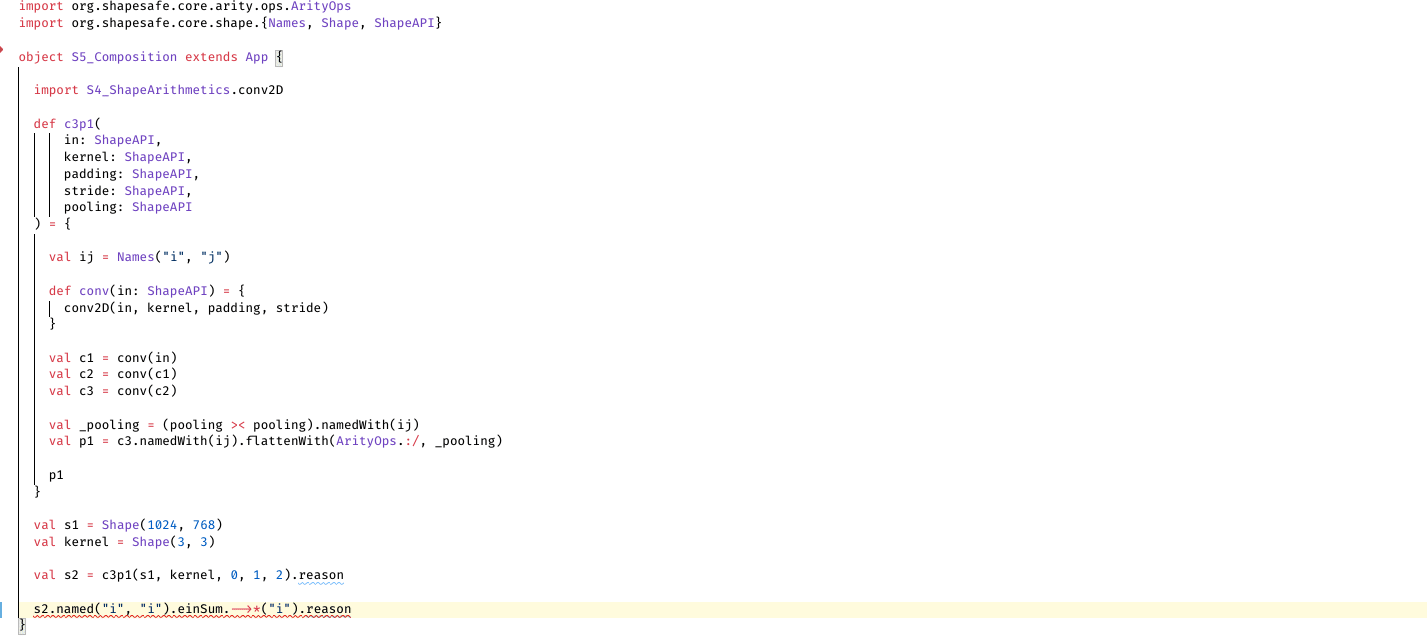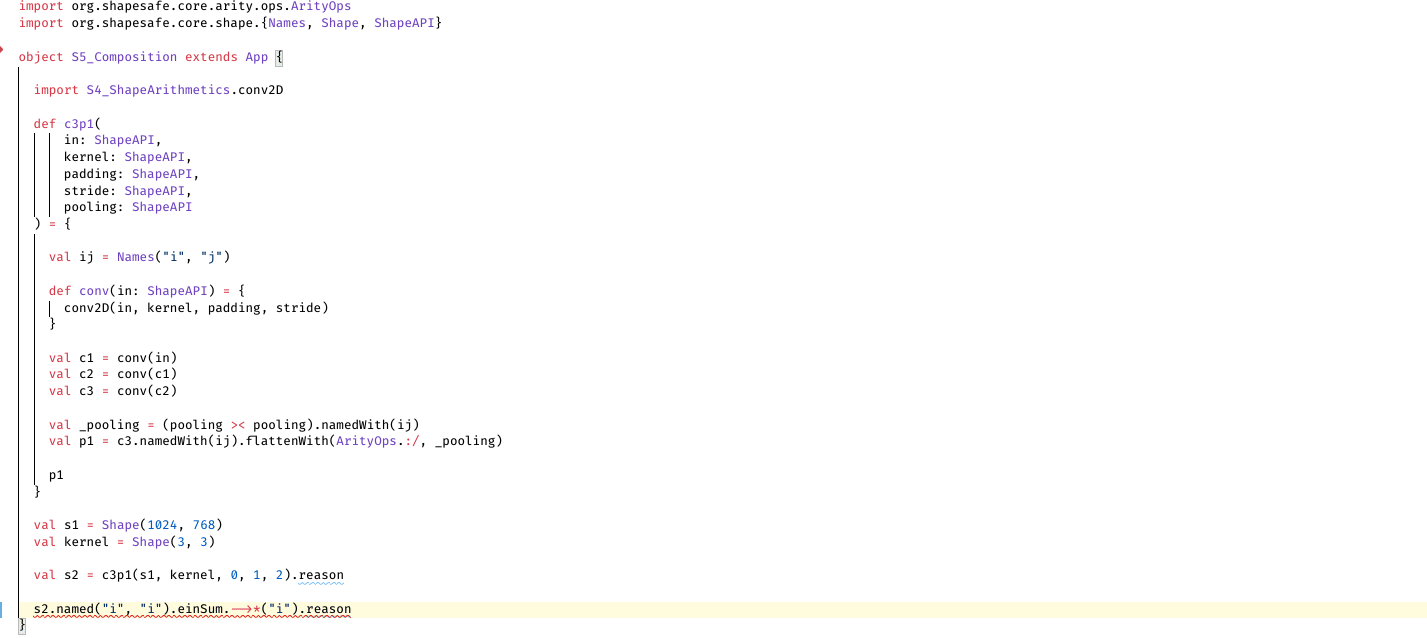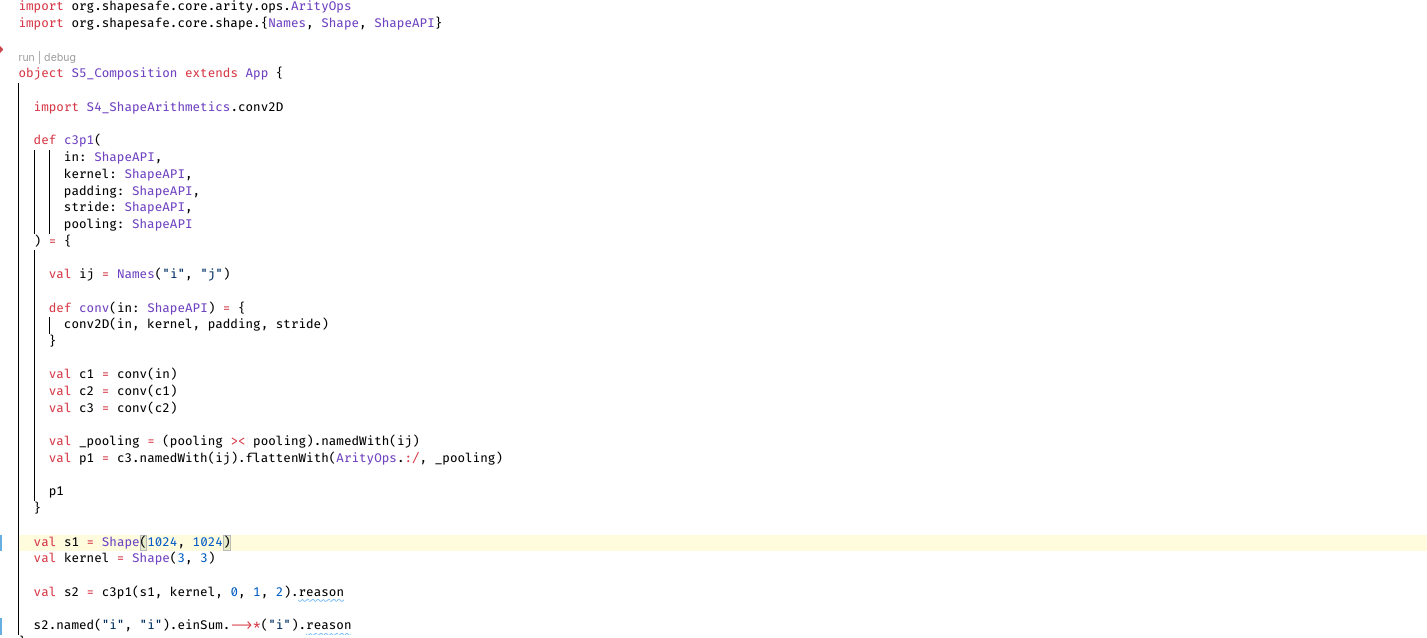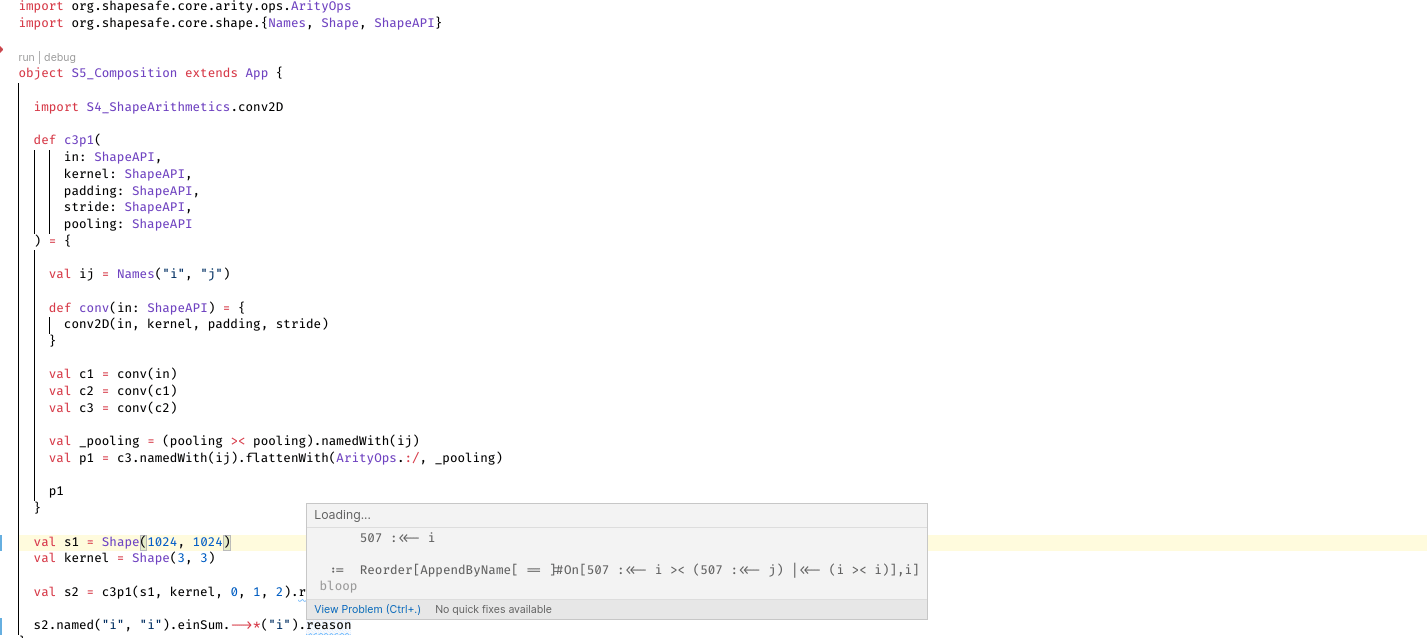
shapesafe is the one-size-fits-all compile-time verifier for numerical linear algebra on JVM, obvious shape and indexing errors in tensor operations are captured by scala's typing system.
Shapesafe allows programs to actively prove themselves while being written. The following capabilities are enabled in release v0.1.0:
tensor contractions & operations that depends on index equality, (all cases of EinSum, dot/cross/matrix/hadamard product)
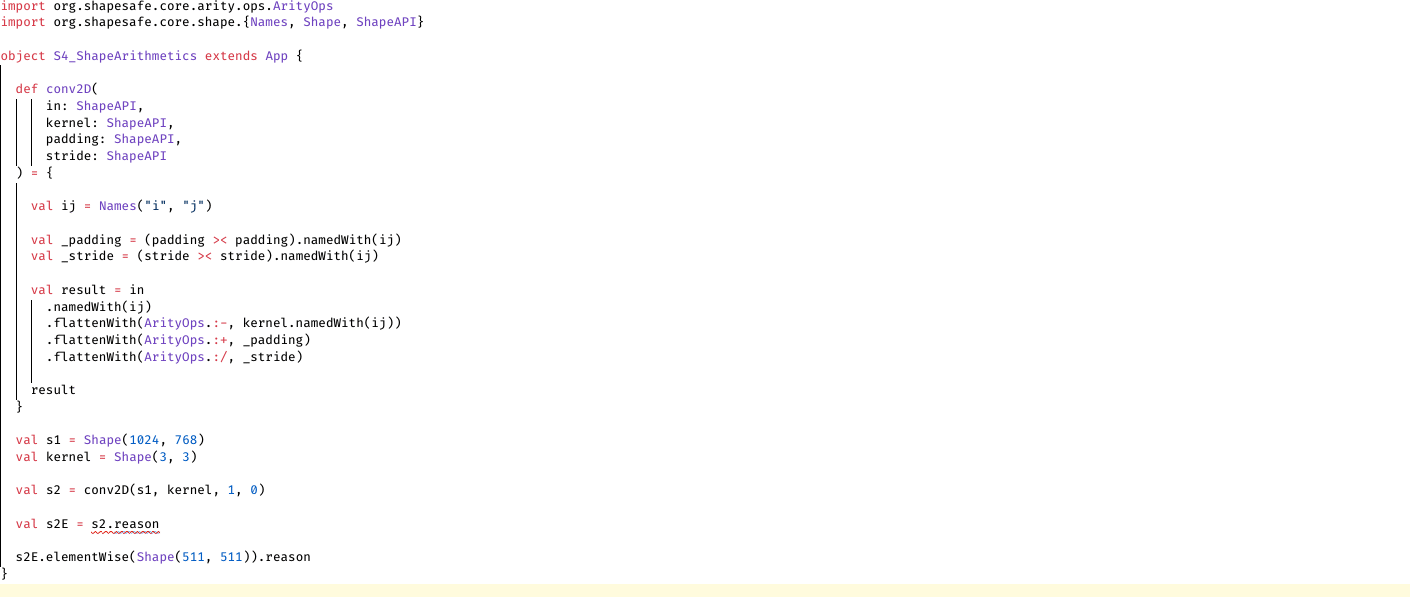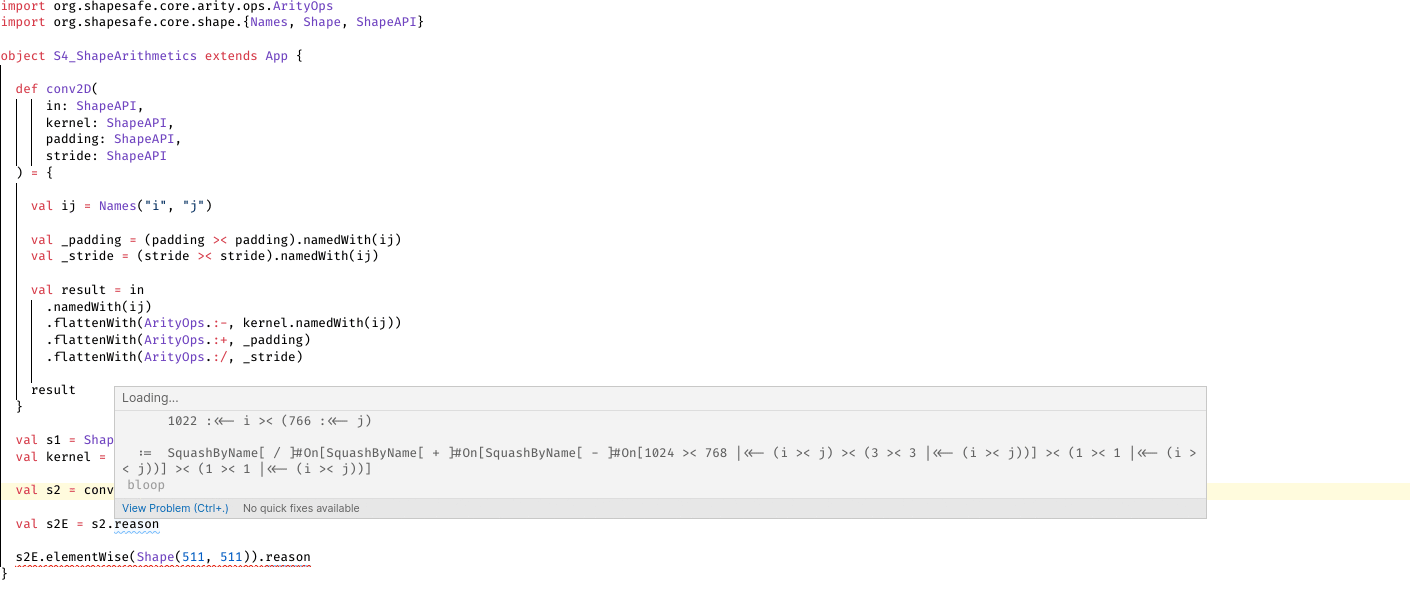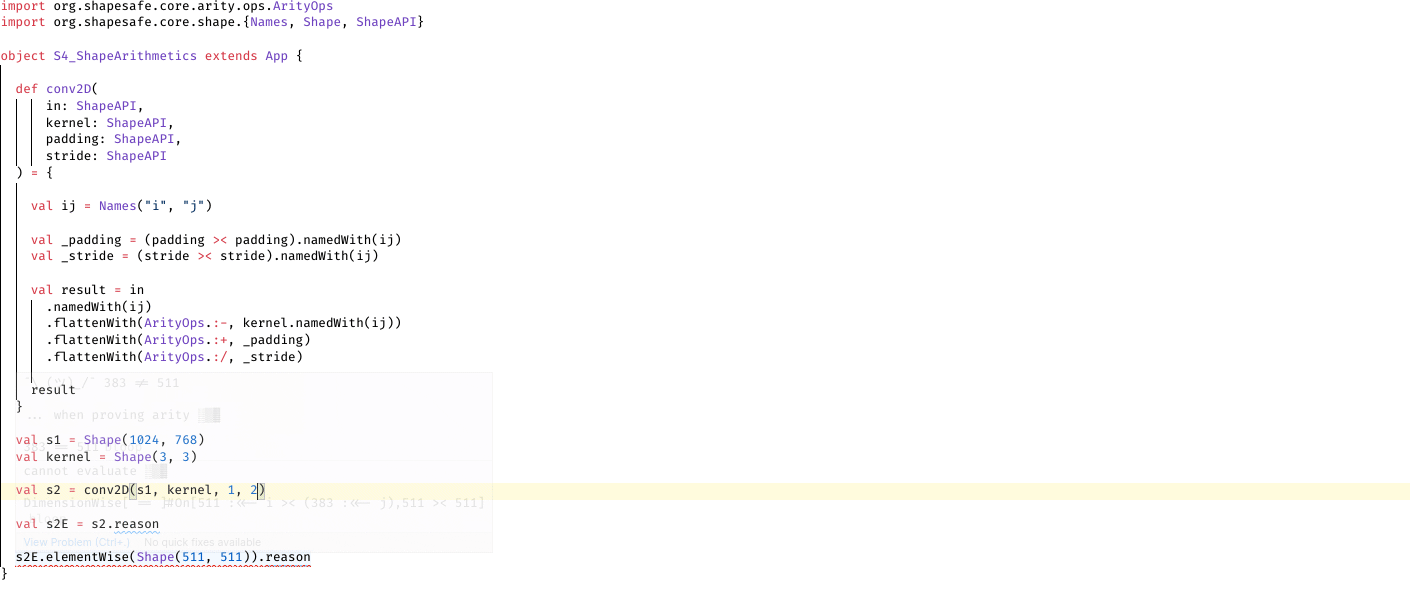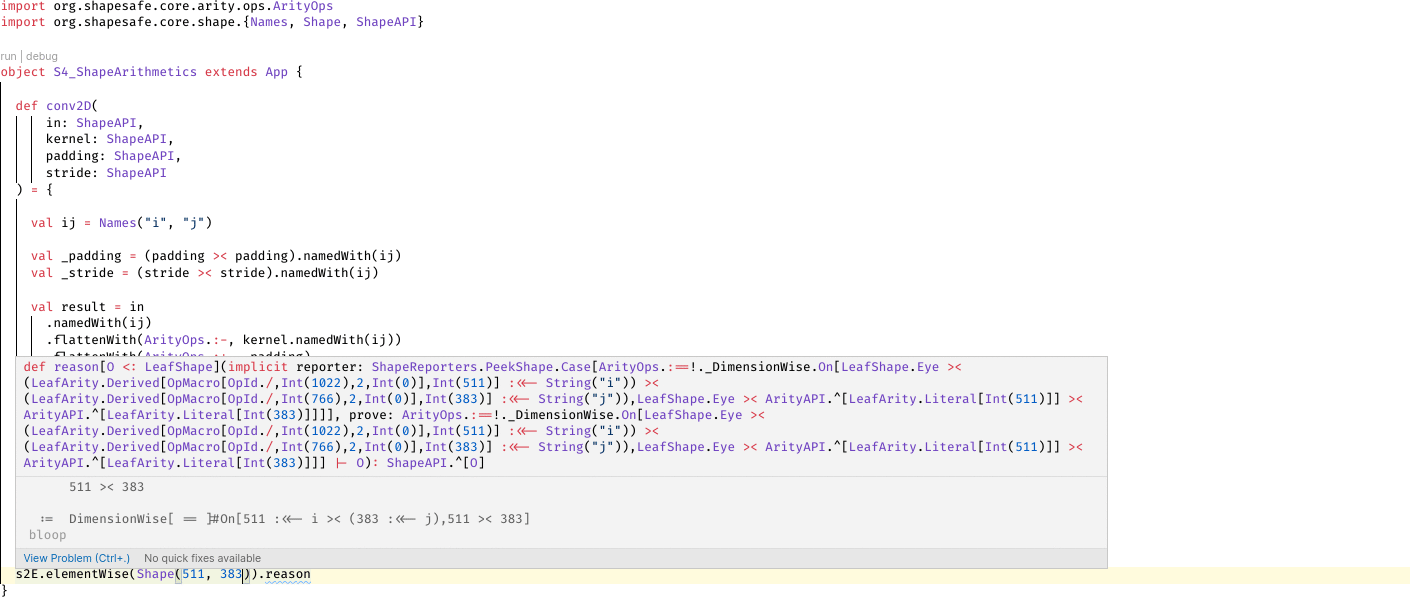
operations that depends on shape arithmetics (convolution, direct sum, kronecker product, flatten/reshape)
These screenshots can be reproduced by compiling our showcases in Visual Studio Code + Scala (Metals) plugin:
It is not a tensor computing library! Instead, it is designed to be embedded into existing libraries to enable less error-prone prototyping (see Roadmap for possible augmentations).
shapesafe started as an experiment to understand intuitionistic type theory used in compiler design, it minimally depends on singleton-ops and shapeless.
Support for scala-2.13 is always guaranteed, supports for scala-2.12 or scala-js should only be enforced intermittently and upon request, please create (or vote for) tickets to backport for a specific compiler.
| branch \ profile | Scala-2.13 | Scala-2.13 w/ splain plugin |
|---|---|---|
| master | ||
| 0.1.4 | ||
| 0.1.3 | ||
| 0.1.2 | ||
| 0.1.1 | ||
| 0.1.0 | ||
| dev (latest WIP) |
-
Setup
shapesafe-corein your scala project using your favourite dependency manager. Replace the version number with that of the latest compatible release -
Compile our Casually Written Tutorial and learn the basics by reading code and errors.
- The shapesafe-demo project provides a reference setup using sbt
- Our Scastie snippet (courtesy of EPFL Scala Center) uses the same setup but can run in browser
- Part 1 - Static Reasoning, Arity Operations
- Part 2 - Shape Operations
- Part 3 - Tensor Typing
- (if the environment timeout please comment out part of the source code and try again)
- Symbolic reasoning for variable dimensions, using Ring/Field axioms and natural deduction
- Type-checking for EinOps
- DJL integration
- DL4j & ND4j integration
- breeze integration (only tensors to up to rank-2 is required)
In POSIX shell, run ./dev/make-all.sh
Guaranteed to be working by Continuous Integration
You must have installed a JDK that supports Gradle 7+ before the compilation
It can be observed immediately in the tutorial that calling functions in shapesafe requires no implicit summoning of type class. In fact, their return types are represented as computation graphs rather than computed Arities or Shapes. As a trade-off, errors in these computation graphs can't be detected as-is:
val a = Shape(1, 2)
val b = Shape(3, 4)
val s1 = (a >< b).:<<=*("i", "j")
s1.peek
// [INFO] 1 >< 2 >< (3 >< 4) :<<= (i >< j)This is a deliberate design which allows complex operand compositions to be defined with no boilerplate (see example above and TutorialPart1/StaticReasoning).
Detection of errors only happens once the expression is evaluated (by explicitly calling .eval or .reason), which summons all algebraic rules like a proof assistant:
s1.eval
// [ERROR] Dimension mismatch
// ...In the above example, calling eval instructs the compiler to summon a series of type classes as lemmata to prove / refute the correctness of the expression:
| lemma | expression | |
|---|---|---|
| (1 >< 2) >< (3 >< 4) :<<= (i >< j) | ||
| (prove outer product) | = | 1 >< 2 >< 3 >< 4 :<<= (i >< j) |
| (refute naming of tensor: Dimension mismatch) | ! |
Evidently, eval can only be used iff. each shape operand in the expression (in the above example a and b) is
either already evaluated, or can be evaluated in the same scope. This is the only case when implicit arguments has to be
declared by the user.
At this moment, all algebraic rules are defined to manipulate the following 2 types of expressions:
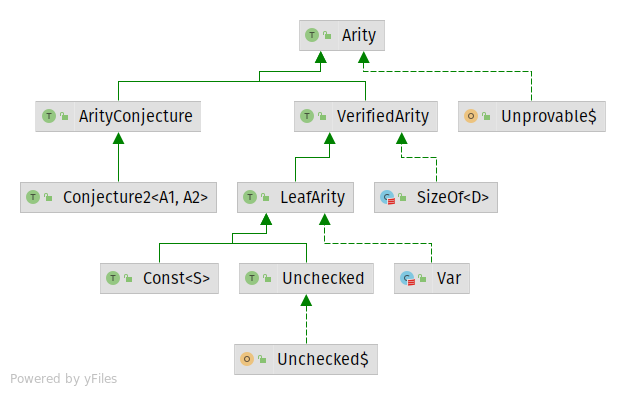
- Arity - describing 1D vectors:
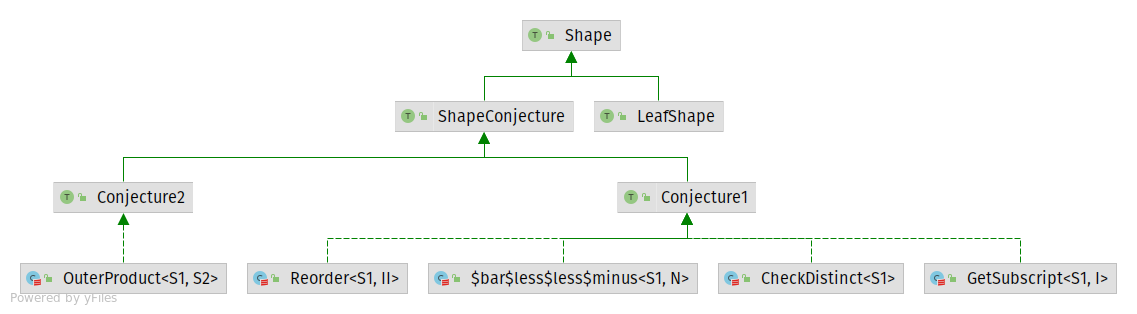
- Shape - describing ND tensors:
Shapesafe works most efficiently if dimensions of all tensors are either constants (represented
by shapesafe.core.arity.Const), or unchecked (represented by shapesafe.core.arity.Unchecked, meaning that it has no
constraint or symbol, and should be ignored in validation). In practice, this can reliably support the majority of
applied linear algebra / ML use cases. Support for symbolic algebra for shape variables (represented
by shapesafe.core.arity.Var) will be gradually enabled in future releases.
Most features in shapeless & singleton-ops are taken over by native compiler features:
- shapeless.Witness → singleton type
- shapeless.Poly → polymorphic function
- singleton.ops.== → inline conditions & matches
- singleton.ops._ → scala.compiletime.ops.*
- shapeless.HList → Tuple
- shapeless.record → Programmatic Structural Types
... but some are still missing:
- Product to Tuple conversion, plus its variants:
- shapeless.NatProductArgs
- shapeless.SingletonProductArgs
- ecosystem: Apache Spark, CHISEL, LMS, typelevel stack, and much more
Scala 3/dotty appears to be vastly more capable as a "proof assistant", with 15~20x speed improvement over Scala 2 on implicit search. This seems to indicate that shapesafe could only achieve large scale, production-grade algebraic verification after the upgrade is finished. At this moment (with Scala 2.13), if the implicit search on your computer is too slow, consider breaking you big operand composition into multiple small ones, and evaluate in-between as often as possible.
- Slide in SBTB2021: https://github.com/tribbloid/shapesafe-demo/raw/main/__presentations/SBTB2021/slide.pdf
- Prof. Dmytro Mitin at National Taras Shevchenko University of Kyiv
- Oron Port et al. maintainers of singleton-ops
- Mile Sabin et al. maintainers of shapeless
- Torsten Schmits et al. maintainers of splain
- Breandan Considine, maintainer of Kotlin∇
This project is heavily influenced by Kotlin∇ (see discussion here) and several pioneers in type-safe ML:
- Evan Spark for showing the possibility first
- Tongfei Chen et al. for Nexus
- Dougal Maclaurin et al. for Dex
- Prof. Austin Huang et al. for HaskTorch
- Maxime Kjaer et al. for tf-dotty
Many have answered critical questions that have guided how the project evolves:
- Torsten Scholak - API, compiler, gradual typing
- Alex Merritt - API, IR, documents
- Cameron Rose - API
- Arseniy Zhizhelev - Scala 3 upgrade
- Ryan Orendorff - Automated theorem proving