This repository contains the source code for the paper Learning Similarity Metrics for Numerical Simulations by Georg Kohl, Kiwon Um, and Nils Thuerey, published at ICML 2020.
LSiM is a metric intended as a comparison method for dense 2D data from numerical simulations. It computes a scalar distance value from two inputs that indicates the similarity between them, where a higher value means they are more different. Simple vector space metrics like an L1 or L2 distance are suboptimal comparison methods, as they only consider pixel-wise comparisons and cannot capture structures on different scales or contextual information. Even though they represent improvements, the commonly used structural similarity (SSIM) and peak signal-to-noise ratio (PSNR) suffer from similar problems.
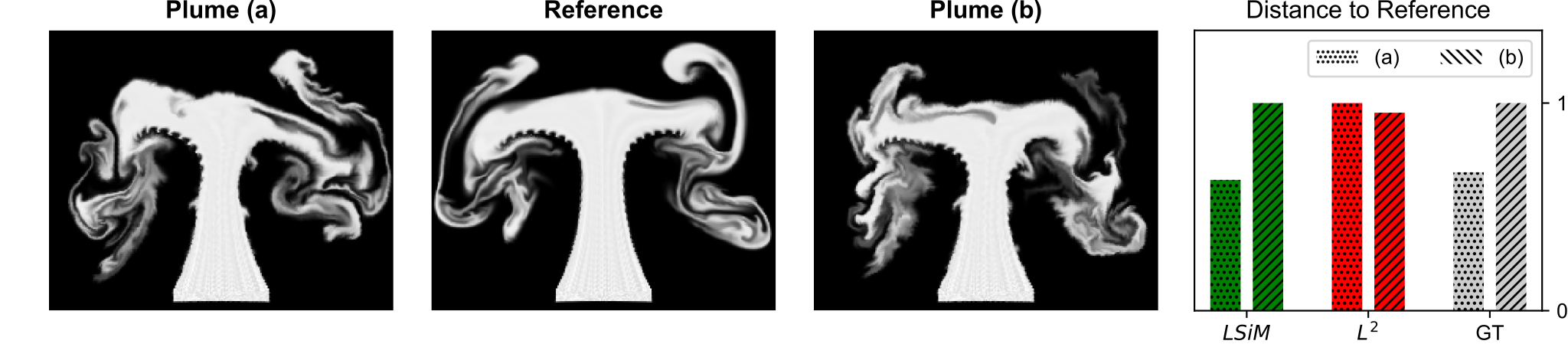 Instead, LSiM extracts deep feature maps from both inputs and compares them. This means similarity on different scales and recurring structures or patterns are considered for the computation. This can be seen in the figure above, where two smoke plumes with different amounts of noise added to the simulation are compared to a reference without any noise. The normalized distances (lower means more similar) on the right indicate that LSiM (green) correctly recovers the ground truth change (GT, grey), while L2 (red) yields a reversed ordering. Furthermore, LSiM guarantees the mathematical properties of a pseudo-metric, i.e., given any three data points A, B, and C the following holds:
Instead, LSiM extracts deep feature maps from both inputs and compares them. This means similarity on different scales and recurring structures or patterns are considered for the computation. This can be seen in the figure above, where two smoke plumes with different amounts of noise added to the simulation are compared to a reference without any noise. The normalized distances (lower means more similar) on the right indicate that LSiM (green) correctly recovers the ground truth change (GT, grey), while L2 (red) yields a reversed ordering. Furthermore, LSiM guarantees the mathematical properties of a pseudo-metric, i.e., given any three data points A, B, and C the following holds:
- Non-negativity: Every computed distance value is in [0,∞]
- Symmetry: The distance A→B is identical to the distance B→A
- Triangle inequality: The distance A→B is shorter or equal to the distance via a detour (first A→C, then C→B)
- Identity of indiscernibles (relaxed): If A and B are identical the resulting distance has to be 0
Further information is available at our project website. To compare scalar or vectorial 3D data, you can have a look at our volumetric metric VolSiM that was specifically designed for this data domain. Feel free to contact us if you have questions or suggestions regarding our work or the source code provided here.
In the following, Linux is assumed as the OS but the installation on Windows should be similar. First, clone this repository to a destination of your choice.
git clone https://github.com/tum-pbs/LSIM
cd LSIM
We recommend to install the required python packages (see requirements.txt) via a conda environment (using miniconda), but it may be possible to install them with pip (e.g. via venv for separate environments) as well.
conda create --name LSIM_Env --file requirements.txt
conda activate LSIM_Env
If you encounter problems with installing, training, or evaluating the metric, let us know by opening an issue.
To evaluate the metric on two numpy arrays arr1, arr2 you only need to load the model and call the computeDistance method. Supported input shapes are [width, height, channels] or [batch, width, height, channels], with one or three channels.
from LSIM.distance_model import *
model = DistanceModel(baseType="lsim", isTrain=False, useGPU=True)
model.load("Models/LSiM.pth")
dist = model.computeDistance(arr1, arr2)
# resulting shapes: input -> output
# [width, height, channel] -> [1]
# [batch, width, height, channel] -> [batch]The inputs are automatically normalized and interpolated to the standard network input size of 224x224 by default. Since the model is fully convolutional different input shapes are possible, and we determined that the metric still works well for spatial input dimensions between 128x128 - 512x512. Outside this range the model performance can drop significantly, and too small inputs can cause issues as the feature extractor needs to reduce the input dimensions.
The input processing can be modified via the optional parameters interpolateTo and interpolateOrder, that determine the resulting shape and interpolation order (0=nearest, 1=linear, 2=cubic). Set both to None to disable the interpolation.
The resulting numpy array dist contains distance values with shape [1] or [batch] depending on the shape of the inputs. If the evaluation should only use the CPU, set useGPU=False. A more detailed example is shown in distance_example.py; to run it use:
python Source/distance_example.py
To evaluate the metric using TensorFlow, loading the model weights from PyTorch into a suitable TensorFlow model implementation is recommended. An example using TensorFlow 1.14 and Keras is shown in convert_to_tf.py. To install TensorFlow in addition to the requirements mentioned above and run the example, use:
conda install tensorflow=1.14
python Source/convert_to_tf.py
The data (3.9 GB .zip file) can be downloaded via any web browser, ftp, or rsync here: https://doi.org/10.14459/2020mp1552055. Alternatively, a direct command line download is possible with:
wget "https://dataserv.ub.tum.de/s/m1552055/download?files=LSIM_2D_Data.zip" -O LSIM_2D_Data.zip
It is recommended to check the archive for corruption, by comparing the SHA512 hash of the downloaded data with the content of the checksums file provided by the data server. If the hashes do not match, restart the download or try a different download method.
sha512sum LSIM_2D_Data.zip
wget "https://dataserv.ub.tum.de/s/m1552055/download?files=checksums.sha512" -O checksums.sha512
Once the download is complete, unzip the file with unzip LSIM_2D_Data.zip. Basic information about the individual data sets can be found in the included README_DATA.txt file, and a more detailed description is provided in paper.
To compare the performance of different metrics on the data, use the metric evaluation in eval_metrics.py:
python Source/eval_metrics.py
It loads multiple metrics in inference mode to compute distances on different data sets, and then evaluates them via the Pearson correlation coefficient or Spearman's ranking correlation (see mode option). The script computes and stores the resulting distances as a numpy array and the corresponding correlation values as a CSV file in the Results directory. The stored distances can be reused for different final evaluations via the loadFile option. Running the metric evaluation without changes should result in values similar to Table 1 in the paper (small deviations due to minor changes in the evaluation are expected, and the optical flow experiment is not included due to compatibility issues).
The necessary steps to re-train the metric from scratch can be found in training.py:
python Source/training.py
Running the training script without changes should result in a model with a performance close to our final LSiM metric (when evaluated with the metric evaluation discussed above). But of course, minor deviations due to the random nature of the model initialization and training procedure may cause performance fluctuations.
Backpropagation, e.g., in the context of training a GAN is straightforward by integrating the DistanceModel class that derives from torch.nn.Module in a new network. Load the trained model weights from the Models directory with the load method in DistanceModel on initialization (see Basic Usage above), and freeze all trainable weights of the metric if required. In this case, the metric model should be called directly instead of using computeDistance to perform the comparison operation. An example for this process based on a simple Autoencoder is shown in backprop_example.py:
python Source/backprop_example.py
If you use the LSiM metric or the data provided here, please consider citing our work:
@inproceedings{kohl2020_lsim,
author = {Kohl, Georg and Um, Kiwon and Thuerey, Nils},
title = {Learning Similarity Metrics for Numerical Simulations},
booktitle = {Proceedings of the 37th International Conference on Machine Learning},
volume = {119},
pages = {5349--5360},
publisher = {PMLR},
year = {2020},
month = {7},
url = {http://proceedings.mlr.press/v119/kohl20a.html},
}
This work was supported by the ERC Starting Grant realFlow (StG-2015-637014). This repository also contains the image-based LPIPS metric from the perceptual similarity repository for comparison.