#everystreet algorithm

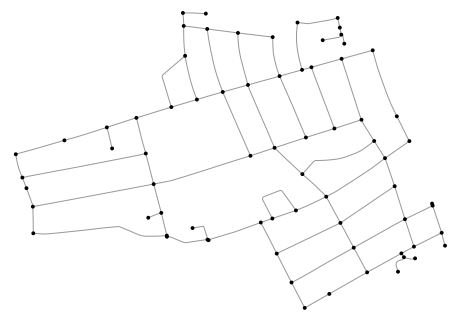
Over the COVID-19 lockdown many runners and cyclist found themselves captured within their cities. Some of them ended up running or spinning endless hours on virtual races such as Zwift, but some as e.g. Mark Beaumont [1] decided to join #everystreet challenge. Every street is a challenge originated by Rickey Gates [2, 3] who run every single street in city of San Francisco in fall 2018 which took him 46 days and run 1,303 miles.

Inspired by Mark Beaumont who did this challenge over the lockdown in Edinburgh, place where I spend the lockdown, and literally everyone else who managed to accomplish this challenge (I would have never had the patience and motivation to run that much in the city) I said to myself that I am a mathematician and software engineer more then a runner or cyclist. So, I ask myself, what is the optimal route? Is there any algorithm which can generate such route?

For more details see the theoretical summary
The app itself can be find: www.everystreetchallenge.com
Jupyter notebook with The Grange example

Every street challenge

Rules of every street challenge are run or cycle every single street of given (metropolitan) area which is usually a city or a neighborhood. Till this point the rules are simple and clear, but the problem is the street definition. How do we define a street? Do we include pedestrian paths, parks or motorways? For simplicity, we consider a street network of edges and nodes (interception of two or more edges and dead-end roads) accessible by car*. Assuming that runner can run oneway roads in both direction, we do not consider road direction. In order to find such network we used Open Street Map API [4].

Chinese postman problem

Finding a route for #everystreet challenge is basically a well-known problem of the chinese postman, called after Chinese mathematician Kuan Mei-Ko. (Also known as Postman Tour or Route Inspection Problem) The problem is to find the shortest closed path (or circuit) such that visits every edge of a (closed and undirected) graph.

from libs.tools import *
from libs.graph_route import plot_graph_route

import networkx as nx
import osmnx as ox
import matplotlib.pyplot as plt

from network import Network
from network.algorithms import hierholzer

We used OSMnx as a source for geographical data. As an example, we chose an Edinburgh neighborhood of the Grange. In order to avoid heavy traffic we specify OSMnx query and limit the highway selection.

CUSTOM_FILTER = (
    '["highway"]["area"!~"yes"]["highway"!~"bridleway|bus_guideway|bus_stop|construction|'
    'cycleway|elevator|footway|motorway|motorway_junction|motorway_link|escalator|proposed|'
    'construction|platform|raceway|rest_area|path|service"]["access"!~"customers|no|private"]'
    '["public_transport"!~"platform"]["fee"!~"yes"]["foot"!~"no"]["service"!~"drive-through|'
    'driveway|parking_aisle"]["toll"!~"yes"]'
)

location = "The Grange, Edinburgh, Scotland"
org_graph = ox.graph_from_place(location, custom_filter=CUSTOM_FILTER)

""" Simplifying the original directed multi-graph to undirected, so we can go both 
    ways in one way streets """
graph = ox.utils_graph.get_undirected(org_graph)
fig, ax = ox.plot_graph(graph, node_zorder=2, node_color="k", bgcolor="w")

Algorithm

In this work, we used algorithm proposed by Edmonds, J. and Johnson [5], which states as follow:

Find all nodes with odd degree
Calculate the sortest distance between all odd-degree nodes
Create a complete weighted graph of all odd-degree nodes, as weights we use distances from step 2.
Find minimal matching in the complete weighted graph
Add matched pairs into original graph
Find the Eulerian circuit using Hierholzer [10] algorithm

👉 For more details see the theoretical summary.

# Finds the odd degree nodes and minimal matching
odd_degree_nodes = get_odd_degree_nodes(graph)
pair_weights = get_shortest_distance_for_odd_degrees(graph, odd_degree_nodes)
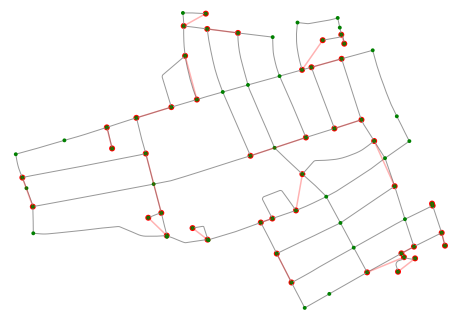
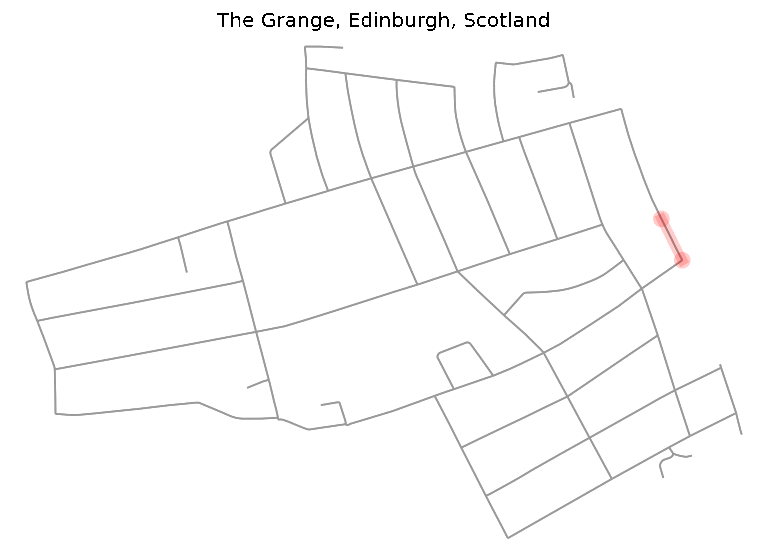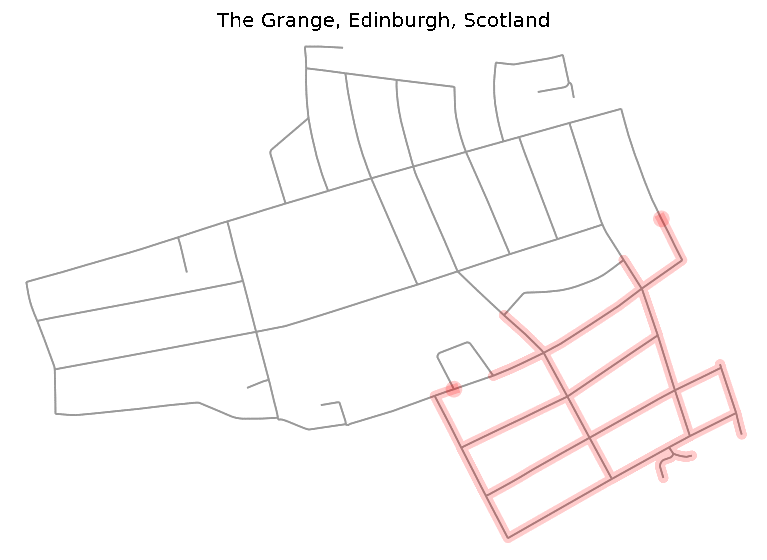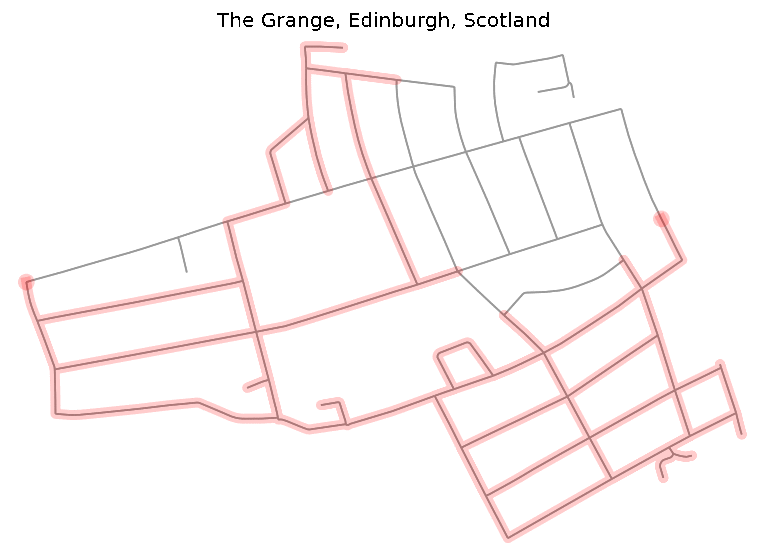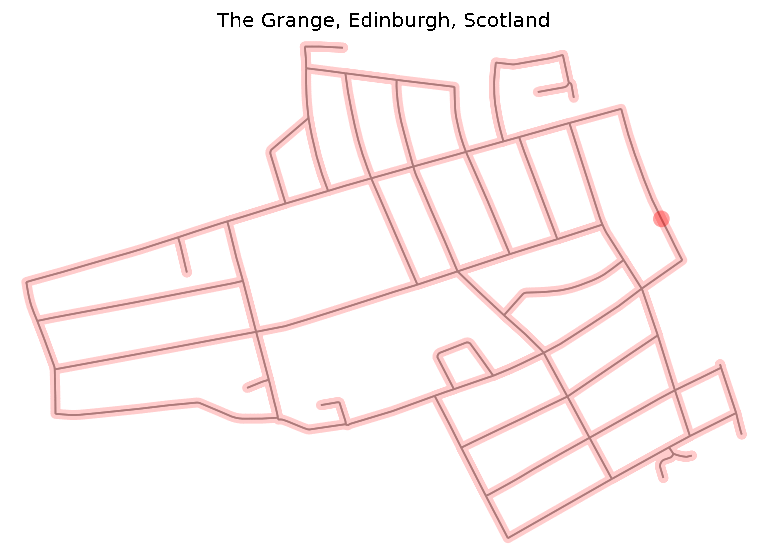
matched_edges_with_weights = min_matching(pair_weights)

Result of minimal matching plotted into original graph (red edges).

fig, ax = plt.subplots(figsize=(8, 8), facecolor='black', frameon=False)
for v, u, w in matched_edges_with_weights:
    x = graph.nodes[v]["x"], graph.nodes[u]["x"]
    y = graph.nodes[v]["y"], graph.nodes[u]["y"]
    ax.plot(x, y, c='red', alpha=0.3)
    ax.scatter(x, y, c='red', edgecolor="none")

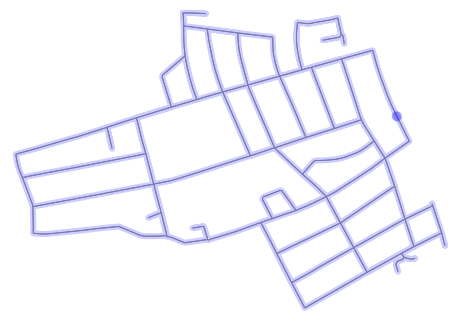
fig, ax = ox.plot_graph(graph, node_zorder=2, node_color='g', bgcolor='k', ax=ax)

Counting the final_path with Hierholzer algorithm and plotting on map. As we can see all edges were visited.

# List all edges of the extended graph including original edges and edges from minimal matching
single_edges = [(u, v) for u, v, k in graph.edges]
added_edges = get_shortest_paths(graph, matched_edges_with_weights)
edges = map_osmnx_edges2integers(graph, single_edges + added_edges)

# Finds the Eulerian path
network = Network(len(graph.nodes), edges, weighted=True)
eulerian_path = hierholzer(network)
converted_eulerian_path = convert_integer_path2osmnx_nodes(eulerian_path, graph.nodes())
double_edge_heap = get_double_edge_heap(org_graph)

# Finds the final path with edge IDs
final_path = convert_path(graph, converted_eulerian_path, double_edge_heap)

fig, ax = plot_graph_route(org_graph, final_path, route_linewidth=6, node_size=0, bgcolor="w", route_alpha=0.2, route_color="w")```

In order to see how the runner should accomplish the route on the map, we created a simple GIF.

for i, e in enumerate(final_path, start=1):
    fig, ax = plot_graph_route(org_graph, final_path[:i], route_linewidth=6, node_size=0, bgcolor="w", route_alpha=0.2)
    ax.set_title(location)
    fig.savefig(f"/img_{i}.png", dpi=120, bbox_inches="tight")

If you would like to generate GPX file with the route, follow Issue #6 (comment)

Usage

In order to run it locally you need to install it on Python +3.8:

pip install -r requirements.txt  # Using pip
poetry install  # or by using Poetry

Feel more that free to use, modify and copy the code, just follow the licence and cite it:

@misc{Kerekrety2020,
  author = {Kerekrety, M},
  title = {#everystreet algorithm},
  year = {2020},
  publisher = {GitHub},
  journal = {GitHub repository},
  howpublished = {\url{https://github.com/matejker/everystreet}}
}

References

[1] Beaumont M. (2020), Strava Profile, https://www.strava.com/athletes/8288853
[2] Gates R. (2019), Every Single Street with Rickey Gates, https://www.everysinglestreet.com/why
[3] Turner K. (2019), Every Single Street, Strava stories, https://blog.strava.com/every-single-street-17484/
[4] Open Street Map (2020), http://openstreetmap.org
[5] Edmonds, J. and Johnson, E.L (1973), Matching, Euler tours and the Chinese postman. Mathematical Programming 5, 88124 https://doi.org/10.1007/BF01580113
[6] Bondy J. A. and Murty U. S. R. (1976), Graph theory with applications, ISBN 0333177916
[7] Diestel. R, (2005), Graph Theory Graduate Texts in Mathematics, Springer
[8] Erben, M., (1652), Knigsberg 1651, https://en.wikipedia.org/wiki/Knigsberg#/media/File:Image- Koenigsberg, Map by Merian-Erben 1652.jpg
[9] Euler L. (1741), Commentarii academiae scientiarum Petropolitanae, Vol- ume 8, pp. 128-140. https://scholarlycommons.pacific.edu/euler-works/53/
[10] Fleischner H. (2016), Algorithms in Graph Theory, https://www.dbai.tuwien.ac.at/staff/kronegger/misc/ AlgorithmsInGraphTheory Script.pdf
[11] Cormen, T. H. (2001), Introduction to algorithms, Cambridge, Mass: MIT Press.
[12] Galil Z. (1986), Efficient algorithms for finding maximum matching in graphs, https://www.semanticscholar.org/paper/Efficient-algorithms-for- finding-maximum-matching-Galil/ef1b31b4728615a52e3b8084379a4897 b8e526ea
[13] Edmonds J. (2008), Weighted maximum matching in general graphs, http://jorisvr.nl/files/graphmatching/20130407/mwmatching.py

twesleyb/everystreet