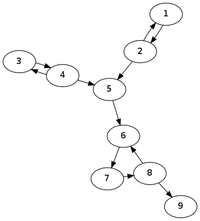
Tarjan's algorithm takes as input a directed (possibly cyclic!) graph and returns as output its strongly connected components in a topological order.
>>> tarjan({1:[2],2:[1,5],3:[4],4:[3,5],5:[6],6:[7],7:[8],8:[6,9],9:[]})
[[9], [8, 7, 6], [5], [2, 1], [4, 3]]
In various cases, dependencies might be cyclic and a group of interdependant actions must be executed simultaneously. It is not uncommon that the simulataneous execution is costly. With Tarjan's algorithm, one can determine an efficient order in which to execute the groups of interdependant actions.
Using Tarjan's algorithm, one can efficiently compute the transitive closure of a graph. (Given a graph G, the transitive closure of G is a graph that contains the same vertices and contains an edge from v to w if and only if there is a path from v to w in G.)
The transitive closure is implemented in tarjan.tc:
>>> tc({1:[2],2:[1,5],3:[4],4:[3,5],5:[6],6:[7],7:[8],8:[6,9],9:[]})
{1: (1, 2, 5, 6, 7, 8, 9),
2: (1, 2, 5, 6, 7, 8, 9),
3: (3, 4, 5, 6, 7, 8, 9),
4: (3, 4, 5, 6, 7, 8, 9),
5: (8, 9, 6, 7),
6: (8, 9, 6, 7),
7: (8, 9, 6, 7),
8: (8, 9, 6, 7),
9: ()}
Given a graph of groups, one can use the transitive closure to determine all indirect members of a group. (Someone is an indirect member of a group, if it is a member of a group that is a member of a group that ... is a member of the group.)
Simply execute
easy_install tarjan
or from this source distribution, run
python setup.py install