/DataScience

Data Science cheat sheet

Statistics

Probability

Expected Value (expectation, mathematical expectation, EV, average, mean value, mean, or first moment)

Arithmetic mean of all the values of the random variable eventually converges to the expected value.

Univariate discrete random variable

Univariate continuous random variable. f the probability distribution of X admits a probability density function f(x), then the expected value can be computed as

Calculating the expected value of a random variable is similar to finding the mean of the whole possible values of the variable (even if it is infinite).

Variance

In probability variance is an expectation of the squared deviation of random variable X from its mean (expected value) .

For discrete random variable

Variance is the square of the standard deviation.

Standard deviation

Standard deviation is a measure of dispersion in data. The standard deviation of a random variable, statistical population, data set, or probability distribution is the square root of its variance. A useful property of the standard deviation is that, unlike the variance, it is expressed in the same units as the data.

Distributions

Normal distribution

Data Visualization

Box plot

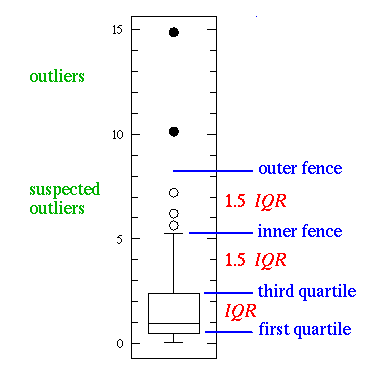
The simplest possible box plot displays the full range of variation (from min to max), the likely range of variation (the IQR), and a typical value (the median). Not uncommonly real datasets will display surprisingly high maximums or surprisingly low minimums called outliers. John Tukey has provided a precise definition for two types of outliers:

  • Outliers are either 3×IQR (inter quartile range) or more above the third quartile or 3×IQR or more below the first quartile.
  • Suspected outliers are are slightly more central versions of outliers: either 1.5×IQR or more above the third quartile or 1.5×IQR or more below the first quartile. If either type of outlier is present the whisker on the appropriate side is taken to 1.5×IQR from the quartile (the "inner fence") rather than the max or min, and individual outlying data points are displayed as unfilled circles (for suspected outliers) or filled circles (for outliers). (The "outer fence" is 3×IQR from the quartile.)

Statistical Models

Regression

Simple Linear Regression

Simple linear model estimates the relation between the dependent and independent variables as a straight line. Simple linear regression model says that the observed value of x differs from its population mean μ by an amount equal to ε. Here ε is an error term which describes the effect on y of all factors other than x.

Here

  1. is the mean value of the dependent variable y when the value of the independent variable is x.
  2. Beta-zero zero is the y-intercept. Beta-zero is the mean value of y when x is equal to 0.
  3. Beta-one is the slope. Beta-one is the change in the mean value of y with an increase of x.
  4. ε is an error term which describes the effect on y of all factors other than x.

Simple linear regression model has to make several assumptions about the error term ε.

Given the population of potential errors at an exact value of X.

  1. The population has mean 0.
  2. The population has variance which is constant for any value of X.
  3. The population is distributed normally.
  4. Any value of the error term ε is statistically independent from other values.

These assumptions imply that since the error term ε is distributed normally and independent from any other values, the itself is distributed normally.

Least squares point estimates (LSPE)

LSPE technique allows to estimate beta-zero and beta-one values by minimizing the sum of the squared distances between Y and .

In simple words, the MSE error of the least squares prediction function is minimized in regards to parameters b0 and b1.

Classification

Nearest Neighbor

Based on the distances between example and training data set. The closest training example votes for the class of the test example. May be based on L1 or L2 distances, etc. Shows good accuracy when data is low-dimensional. No training required. Computationally expensive at the test time.

K-Nearest Neighbor

k closest training examples vote for the class of the test example.

Applying kNN in practice:

  • Normalize the features to have zero mean and unit variance.
  • If data is very high-dimensional, consider using a dimensionality reduction technique such as PCA or even Random Projections.
  • If kNN classifier is running too long, consider using an Approximate Nearest Neighbor library (e.g. FLANN) to accelerate the retrieval (at cost of some accuracy).

Model validation & evaluation

Validation

  1. Cross-validation. Splitting training data into n folds in order to validate the model's accuracy on the different folds and average the results. The model is trained on n - 1 folds each time and validated over the last fold. If the number of validation examples is low, it is better to use cross-validation. Otherwise, single 10-50% validation split is preferred.

Neural networks

Layers

Embedding

Embedding layer represents each instance of the input population as a vector in the output dimension.

W("cat")=(0.2, -0.4, 0.7, ...) 
W("mat")=(0.0, 0.6, -0.1, ...)

These vectors are the optimization parameters of the layer. An interesting side-effect of the embedding is that the layer can learn complex relationships between instances of the input population.

t-SNE visualization of the embedding space

Optimizers

  1. Gradient descent - first-order optimization algorithm to find a local minimum of the function. Based on taking iterative steps towards the opposite direction of the function's gradient at the current position.
  2. Batch gradient descent - gradient of the cost function is calculated by averaging gradients of cost function applied to each individual training example.
  3. Stochastic gradient descent - gradient of the cost function is estimated by computing it over a relatively small sample of data. One epoch of training means that all training inputs were used (our network has seen all the training data).
  4. Hessian technique - descent step is calculated by multiplying gradient on the inverted Hessian matrix of second derivatives (which contains more information about gradient). This leads to fewer steps needed to achieve local minimum. However, this requires heavy matrix calculations.
  5. Momentum-based gradient descent - some sort of an accumulation of the descent is introduced. Much like the real velocity. There is also a friction factor (called momentum coefficient).
  6. Adam ??

Activations

  1. Perceptron - the activation is whether 0 or 1

  2. Sigmoid - 1 / (1 + exp(-z)) [0; 1]

  3. Tanch - (1+tanh(z/2))/2 [-1; 1] Allows negative activations. May perform better if model has negative inputs

  4. ReLU - max(0, z). - Never saturates while z>0. Stops learning if z<0. Known to perform better in image classification.

    Advantages:

    • Biological plausibility: One-sided, compared to the antisymmetry of tanh.
    • Sparse activation: For example, in a randomly initialized network, only about 50% of hidden units are activated (having a non-zero output).
    • Efficient gradient propagation: No vanishing or exploding gradient problems.
    • Efficient computation: Only comparison, addition and multiplication.
    • Scale-invariant: max(0,ax)=a*max(0,x)

    For the first time in 2011, the use of the rectifier as a non-linearity has been shown to enable training deep supervised neural networks without requiring unsupervised pre-training. Rectified linear units, compared to sigmoid function or similar activation functions, allow for faster and effective training of deep neural architectures on large and complex datasets.

    Problems:

    • Non-differentiable at zero: however it is differentiable anywhere else, including points arbitrarily close to (but not equal to) zero.
    • Non-zero centered
    • Unbounded : Could potentially blow up.
    • Dying Relu problem: Relu neurons can sometimes be pushed into states in which they become inactive for essentially all inputs. In this state, no gradients flow backward through the neuron, and so the neuron becomes stuck in a perpetually inactive state and "dies." In some cases, large numbers of neurons in a network can become stuck in dead states, effectively decreasing the model capacity. This problem typically arises when the learning rate is set too high.

  5. Softplus - A smooth approximation to the rectifier. f(x)=ln(1+e^x)