This repository contains Lua implementations of some 2D computational geometry algorithms that I developed during my master's degree classes oriented by Prof. Waldemar Celes, such as:
- Enclosing Circle
- Convex Hull
- Dual Graph Mesh
- Delaunay Triangulation
It also includes the matplotlua, a Lua binding to the matplotlib library.
It is organized as follows:
.
├── algorithms/ # Implementations of the algorithms.
├── datasets/ # Datasets used in the examples.
├── examples/ # Usage examples for each algorithm.
├── figures/ # Output directory for results (images and animations).
├── matplotlua/ # matplotlua library.
└── reports/ # Reports on the algorithms implementations.
# Lua deps
apt install lua5.3 lua-cjson lua-argparse
# Python deps (only necessary for plotting)
apt install python-is-python3 python3-matplotlib
# imagemagick (only necessary to generate step by step animations)
apt install imagemagick-6.q16
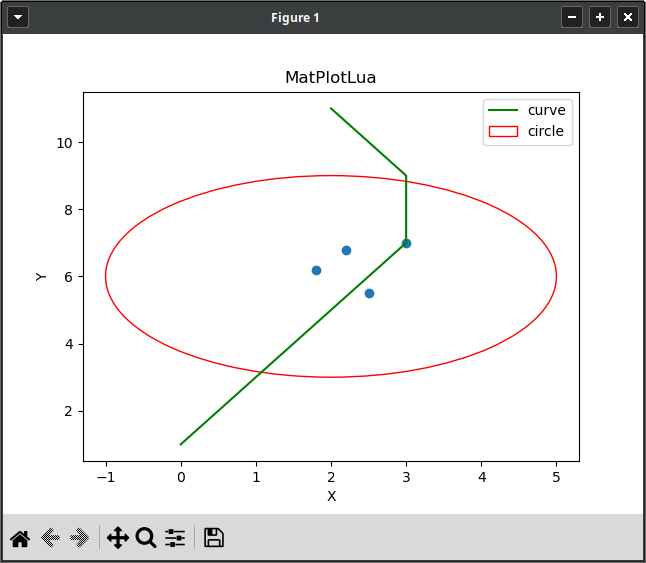
matplotlua is a (very basic) Lua binding to the matplotlib library.
It keeps the plot state in a Lua table until a call to Plot.plot() or Plot.figure() is made. When this happens, the state is dumped to JSON format and piped to a Python script that generates the plot using matplotlib.
(There is probably a better way of doing this, and suggestions are welcome!)
The library is self-contained in the matplotlua/ directory and can be used independently of this repository. It can draw points, lines, curves, polygons and graphs.
A simple usage is shown in matplotlua/main.lua and a more advanced one (including gif generation using imagemagick) can be found in examples/convex_hull.lua (see the -h).
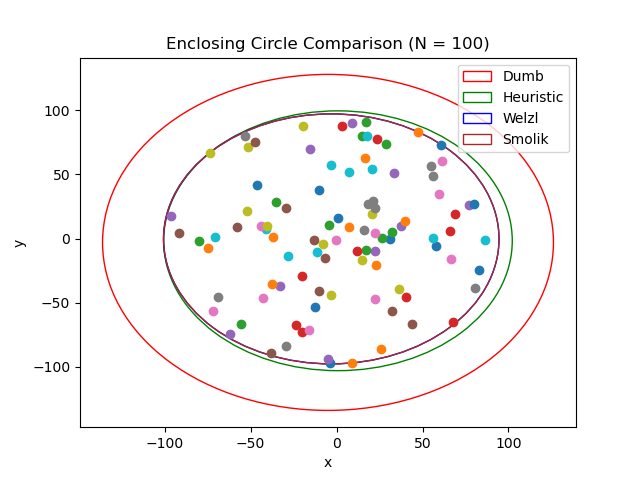
Enclosing circle algorithms find the smallest circle that contains all the points in a set. This is useful for many applications, such as collision detection.
More on the enclosing circle problem here.
Available algorithms:
- Dumb algorithm - O(n), poor results;
- Brute Force - O(n^4), optimal results;
- Heuristic - O(n), good results, but not optimal;
- Welzl's algorithm - O(n) (statistically), optimal results;
- Smolik's algorithm - O(n) (statistically), optimal results, fastest method.
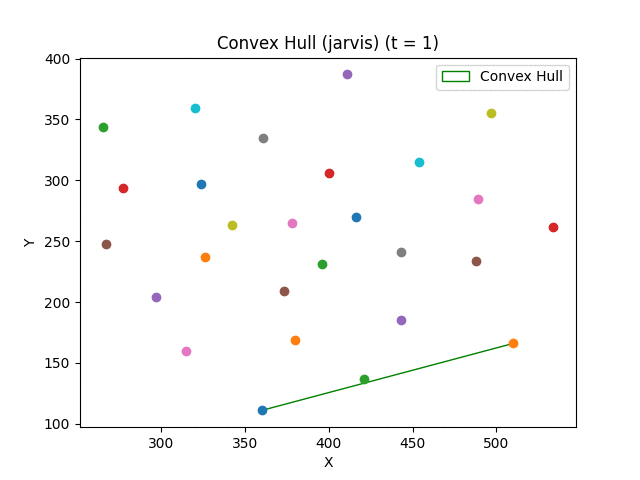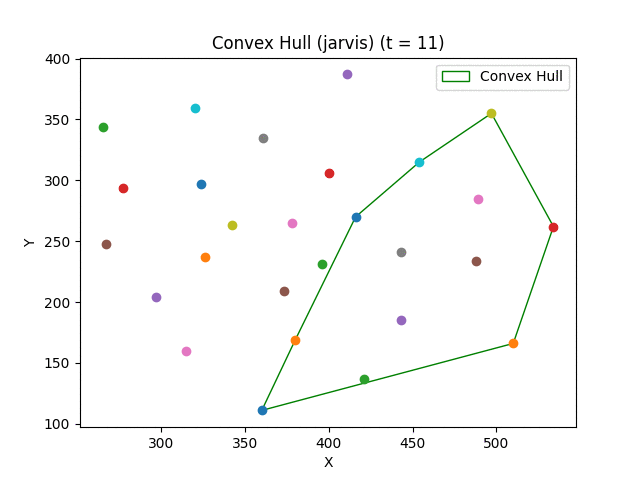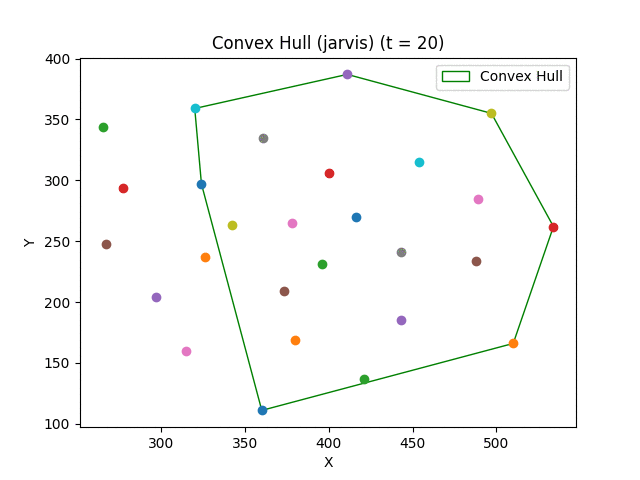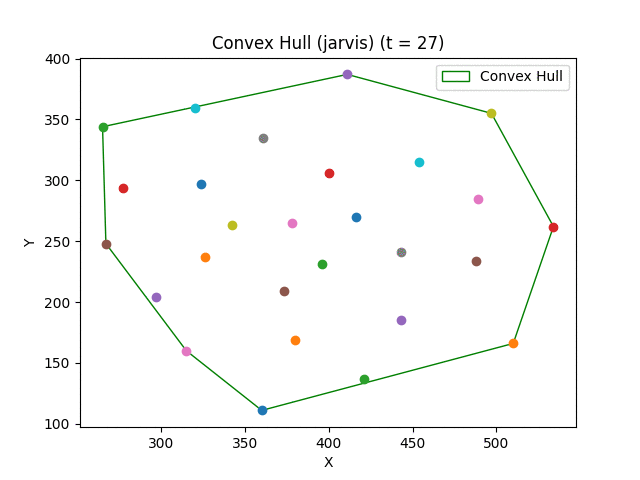
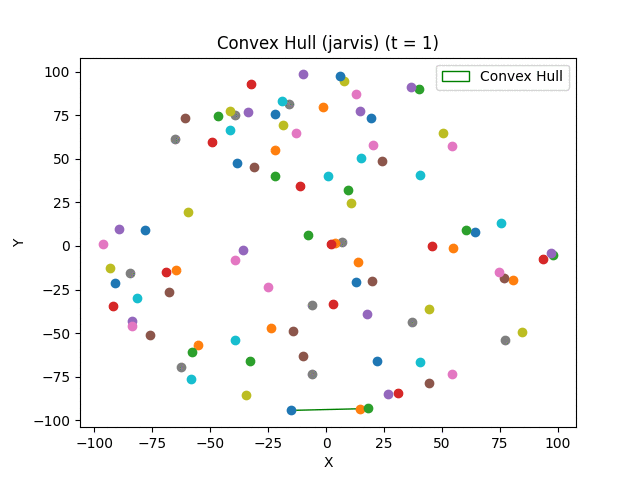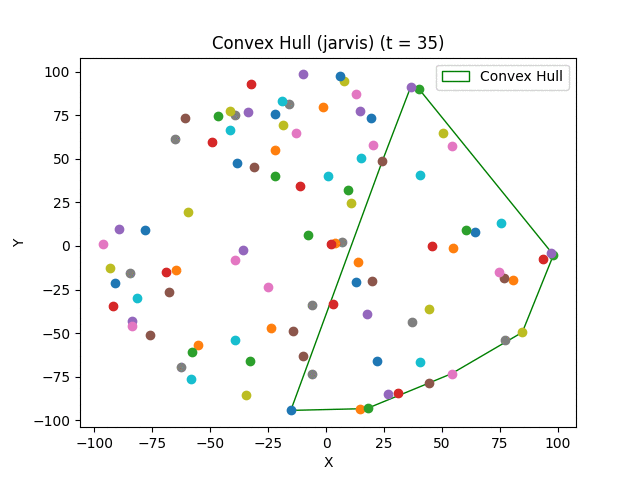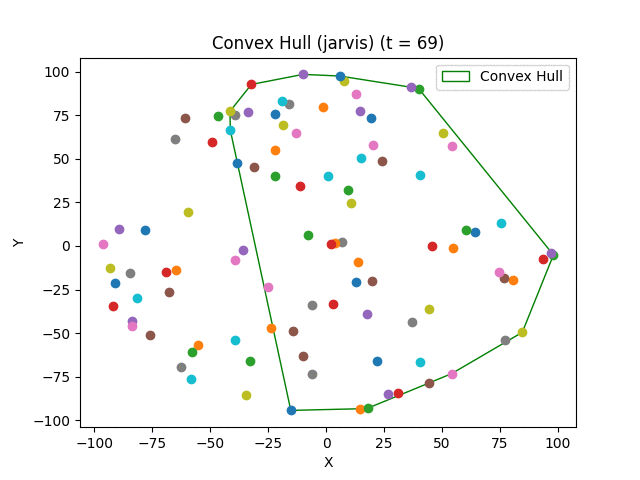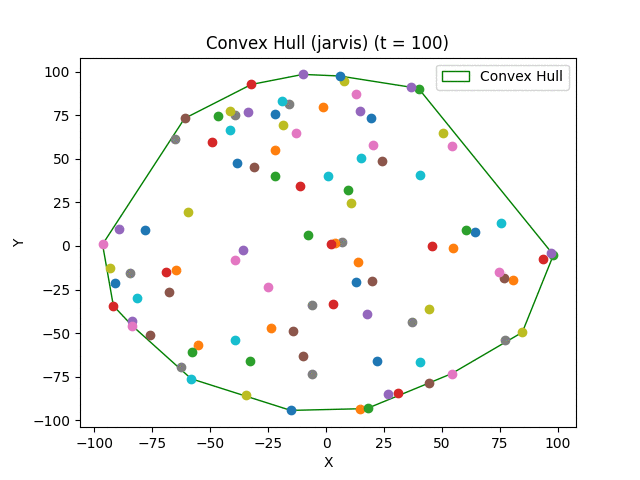
Convex hull algorithms find the smallest convex polygon that contains all the points in a set.
More on the convex hull problem here.
Available algorithms:
- Jarvis March (Gift Wrapping) - O(nh) where h is the number of points in the hull;
- Skala's algorithm - O(n) in practice for most cases.
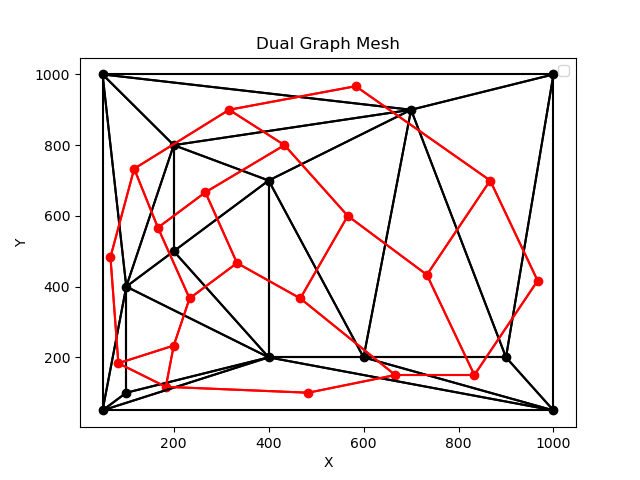
A dual graph mesh is a graph where the vertices are the faces of the original graph and the edges are the shared edges between the faces. This is useful for mesh processing algorithms, including Delunay triangulation. This repository contains a very simple implementation of a dual graph mesh.
More on the dual graph mesh problem here.
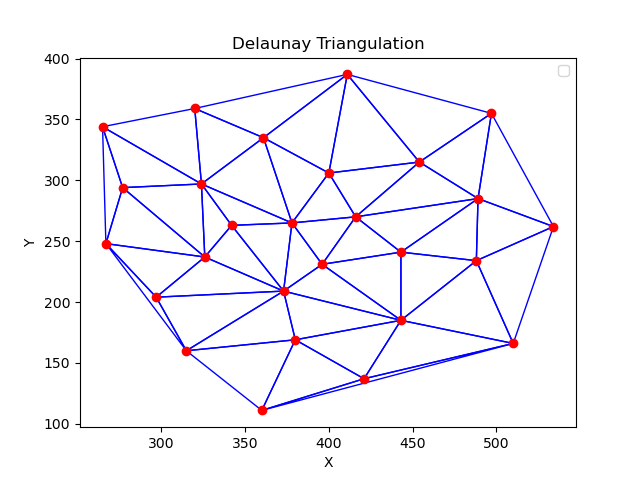
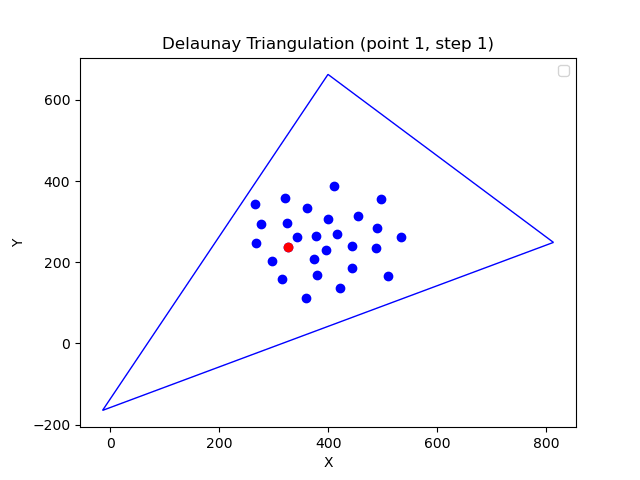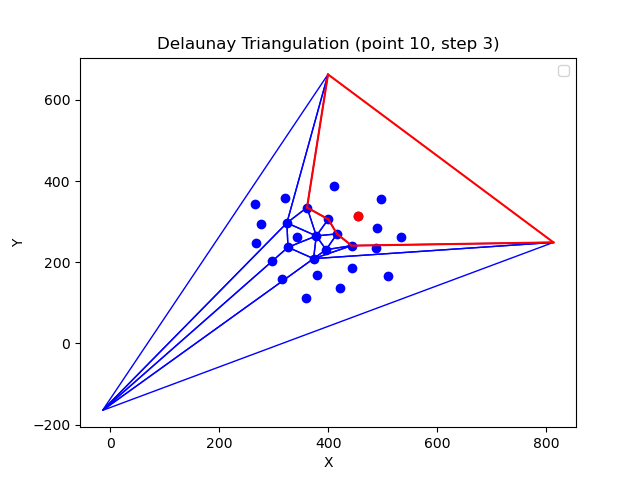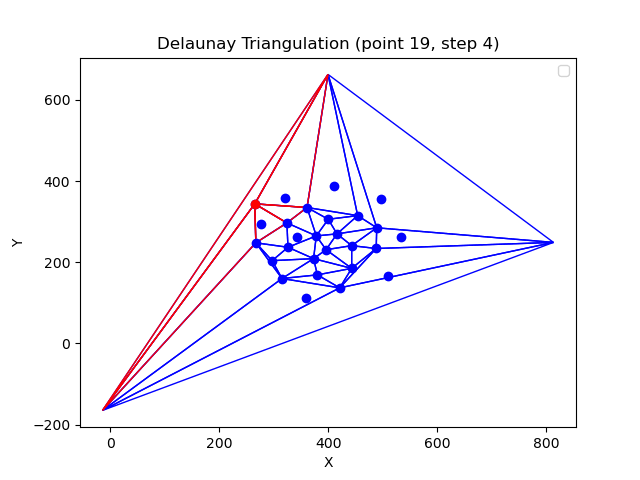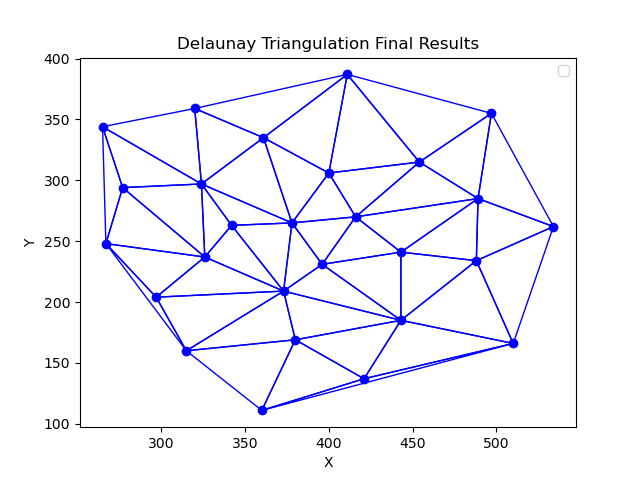
Delunay triangulation is a triangulation of a set of points such that no point is inside the circumcircle of any triangle.
More on the Delaunay triangulation problem here.
Available algorithms:
- Bowyer-Watson - O(n^2) in this implementation. Could be O(nlogn) using a topological data structure.
Some examples can generate step by step animations of the algorithms. To do so, you need to have imagemagick installed and follow the help message of the example.
-
Delaunay Bowyer-Watson algorithm step by step:
-
Convex Hull Jarvis algorithm step by step:
More animations can be found in the figures/ directory.