vathymut/dsos

Dataset shift with outlier scores

D-SOS: Dataset shift with outlier scores

Overview

dsos tests for no adverse shift based on outlier scores. Colloquially, these tests check whether the new sample is not substantively worse than the old sample, not if the two are equal as tests of equal distributions do. dsos implements a family of two-sample comparison which assumes that we have both a training set, the reference distribution, and a test set.

Installation

The package is under active development. From GitHub (which includes recent improvements), install with:

# install.packages("remotes")
remotes::install_github("vathymut/dsos")

The package is also on CRAN, although the CRAN release may lag behind GitHub updates. From CRAN, install the package with:

install.packages("dsos")

Quick Start

Simulate outlier scores to test for no adverse shift when the null (no shift) holds. First, we use the frequentist permutation test:

library(dsos)
set.seed(12345)
n <- 6e2
os_train <- rnorm(n = n)
os_test <- rnorm(n = n)
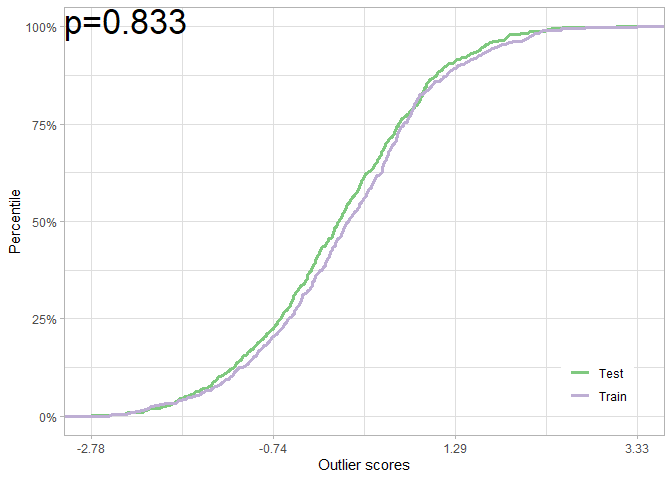
null_pt <- pt_from_os(os_train, os_test)
plot(null_pt)

We can also use the (faster) asymptotic test:

null_at <- at_from_os(os_train, os_test)
plot(null_at)

Doing the same exercise the Bayesian way (with Bayes factors):

null_bf <- bf_from_os(os_train, os_test)
# plot(null_bf)
as_pvalue(null_bf$bayes_factor)
#> [1] 0.903

In all cases, we fail to reject the null of no adverse shift. Note how we can convert a Bayes factor into a $p$-value.

We can repeat this exercise when there is an adverse shift. Again, with the permutation test:

os_shift <- rnorm(n = n, mean = 0.2)
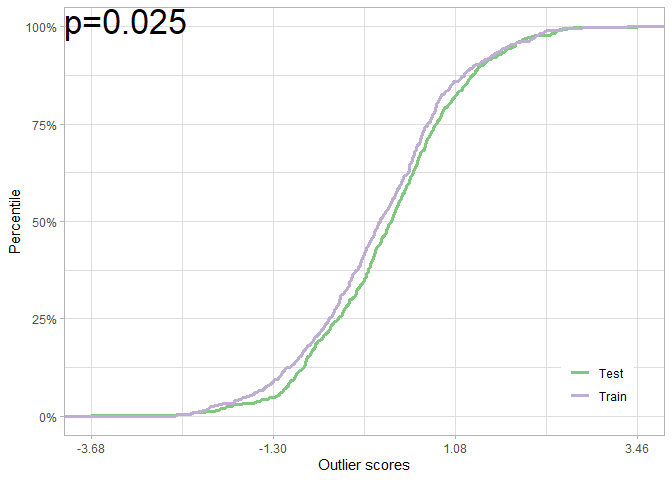
shift_pt <- pt_from_os(os_train, os_shift)
plot(shift_pt)

Once more, with the asymptotic test:

shift_at <- at_from_os(os_train, os_shift)
plot(shift_at)

Doing it the Bayesian way (with Bayes factors):

shift_bf <- bf_from_os(os_train, os_shift)
# plot(shift_bf)
as_pvalue(shift_bf$bayes_factor)
#> [1] 0.0215

We would reject the null of no adverse shift in all cases: the test set is worse off relative to the reference (training) scores.

The function bf_compare is handy: it computes and contrasts Bayes factors for the frequentist and Bayesian approach.

shift_all <- bf_compare(os_train, os_shift)
shift_all
#> $bayes_perm
#> [1] 37.46154
#> 
#> $bayes_noperm
#> [1] 43.44444
#> 
#> $frequentist
#> [1] 30.25

Reference

To cite this work, please refer to the paper. Sample Bibtex is below:

@inproceedings{kamulete2022test,
  title     = {Test for non-negligible adverse shifts},
  author    = {Vathy M. Kamulete},
  booktitle = {The 38th Conference on Uncertainty in Artificial Intelligence},
  year      = {2022},
  url       = {https://openreview.net/forum?id=S5UG2BLi9xc}
}

I gave a talk introducing the dsos R package at useR! 2022 during the ‘Unique Applications and Methods’ track. It is a 15-minute crash course, focused on interpretation. I also wrote a blog post to motivate the need for tests of adverse shift.