FindBounce is a Mathematica package that computes the bounce configuration needed to compute the false vacuum decay rate with multiple scalar fields.
We kindly ask the users of the package to cite the two papers that describe the working of the FindBounce package: the paper with the original proposal by Guada, Maiezza and Nemevšek (2019) and the software release manual by Guada, Nemevšek and Pintar (2020).
To use the FindBounce package you need Mathematica version 10.0 or later.
The package is released in the .paclet file format that contains the code, documentation and other necessary resources.
Download the latest .paclet file from the repository "releases" page
to your computer and install it by evaluating the following command in the Mathematica:
(* Path to .paclet file downloaded from repository "releases" page. *)
PacletInstall["full/path/to/FindBounce-X.Y.Z.paclet"]This will permanently install the FindBounce package to $UserBasePacletsDirectory.
Mathematica will always use the latest installed version of the package and all installed versions
can be enumerated by evaluating PacletFind["FindBounce"].
You can get more detailed information about the package with PacletInformation["FindBounce"].
All versions can be uninstalled with:
PacletUninstall["FindBounce"]After installing the paclet, load it in the Mathematica session with Needs.
To access the documentation, open the notebook interface help viewer and search for "FindBounce".
The first time after package installation, sometimes Mathematica needs to
be restarted to update the documentation search index.
Needs["FindBounce`"]To begin, let us define a single field potential, find its extrema and plot it.
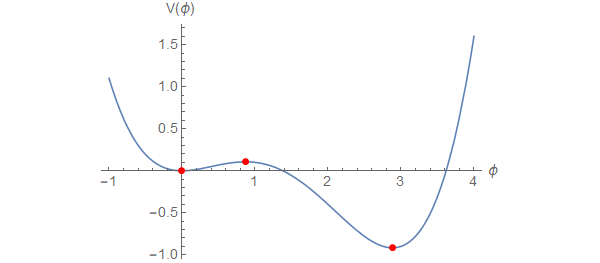
potential[x_] := 0.5 x^2 - 0.5 x^3 + 0.1 x^4;
extrema = Block[{x}, x /. NSolve[D[potential[x], x] == 0, x]]
(* {0., 0.867218, 2.88278} *)
pts = Transpose[{extrema, potential /@ extrema}]
Plot[
potential[x],
{x, -1, 4},
Epilog -> {Red, PointSize[Large], Point[pts]}
]Now we simply evaluate the FindBounce function on this potential going from one minimum to the other.
The results are stored in a BounceFunction object, that stores the results of the calculation
and properties of the solution, like the Euclidean action.
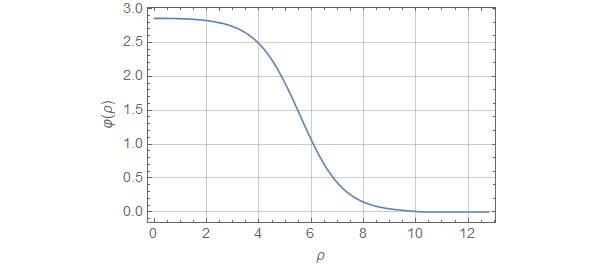
bf = FindBounce[potential[x], {x}, { extrema[[1]], extrema[[3]] }]
(* BounceFunction[...]*)
bf["Action"]
(* 1515.5 *)
bf["Dimension"]
(* 4 *)The field configuration can also be easily plotted with BouncePlot function.
BouncePlot[bf]We define a two field potential V with known minima locations and
calculate its bounce configuration. Option "MidFieldPoint" defines
the point which is included in the initial path.
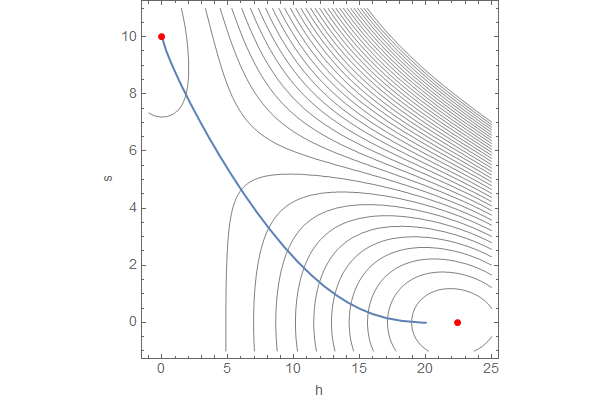
V[h_,s_]:= -100 h^2 + 0.1 h^4 - 60 s^2 + 0.3 s^4 + 3 h^2 s^2;
minima = {{0.,10.},{22.4,0.}};
bf = FindBounce[V[h,s],{h,s}, minima, "MidFieldPoint"-> {6.,6.}]Then we plot potential with contours, locations of minima (red points) and the final trajectory of the bounce field.
{rInit,rFin} = MinMax@bf["Radii"];
Show[
ContourPlot[
V[h,s],{h,-1,25},{s,-1,11},
Contours->40,
ContourShading->None,
ContourStyle->Gray,
Epilog->{PointSize[Large],Red,Point[minima]}
],
ParametricPlot[Through@bf["Bounce"][r],{r,rInit,rFin}]
]We can also plot the final bounce field configuration for both fields.
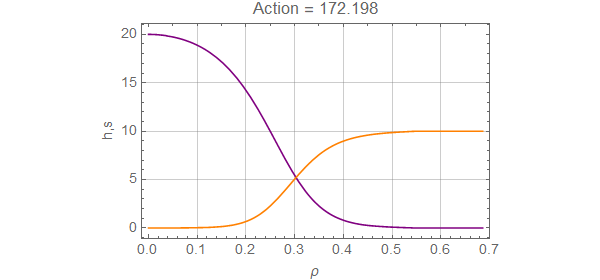
BouncePlot[bf,
PlotLabel-> Row[{"Action = ",bf["Action"]}],
PlotStyle-> {Purple, Orange},
]Please use the repository "issues" page to submit bugs or feature ideas.
If you find this package useful, feel free to send feedback by email to victor.guada(at)ijs.si.
Pull requests to this repository are welcome.
For major changes, please open an issue first to discuss what you would like to change.
Instructions on building the .paclet file from source code can be found in CONTRIBUTING.md file.