This repository contains JavaScript based examples of many popular algorithms and data structures.
Each algorithm and data structure has its own separate README with related explanations and links for further reading (including ones to YouTube videos).
Read this in other languages: 简体中文, 繁體中文
A data structure is a particular way of organizing and storing data in a computer so that it can be accessed and modified efficiently. More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data.
B - Beginner, A - Advanced
BLinked ListBQueueBStackBHash TableBHeapBPriority QueueATrieATreeABinary Search TreeAAVL TreeARed-Black TreeASegment Tree - with min/max/sum range queries examplesAFenwick Tree (Binary Indexed Tree)
AGraph (both directed and undirected)ADisjoint Set
An algorithm is an unambiguous specification of how to solve a class of problems. It is a set of rules that precisely define a sequence of operations.
B - Beginner, A - Advanced
- Math
BFactorialBFibonacci NumberBPrimality Test (trial division method)BEuclidean Algorithm - calculate the Greatest Common Divisor (GCD)BLeast Common Multiple (LCM)AInteger PartitionBSieve of Eratosthenes - finding all prime numbers up to any given limitBIs Power of Two - check if the number is power of two (naive and bitwise algorithms)ALiu Hui π Algorithm - approximate π calculations based on N-gons
- Sets
BCartesian Product - product of multiple setsAPower Set - all subsets of a setAPermutations (with and without repetitions)ACombinations (with and without repetitions)BFisher–Yates Shuffle - random permutation of a finite sequenceALongest Common Subsequence (LCS)ALongest Increasing SubsequenceAShortest Common Supersequence (SCS)AKnapsack Problem - "0/1" and "Unbound" onesAMaximum Subarray - "Brute Force" and "Dynamic Programming" (Kadane's) versions
- Strings
ALevenshtein Distance - minimum edit distance between two sequencesBHamming Distance - number of positions at which the symbols are differentAKnuth–Morris–Pratt Algorithm - substring searchARabin Karp Algorithm - substring searchALongest Common Substring
- Searches
- Sorting
BBubble SortBSelection SortBInsertion SortBHeap SortBMerge SortBQuicksort - in-place and non-in-place implementationsBShellsortACounting SortARadix Sort
- Trees
BDepth-First Search (DFS)BBreadth-First Search (BFS)
- Graphs
BDepth-First Search (DFS)BBreadth-First Search (BFS)ADijkstra Algorithm - finding shortest path to all graph verticesABellman-Ford Algorithm - finding shortest path to all graph verticesADetect Cycle - for both directed and undirected graphs (DFS and Disjoint Set based versions)APrim’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graphBKruskal’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graphATopological Sorting - DFS methodAArticulation Points - Tarjan's algorithm (DFS based)ABridges - DFS based algorithmAEulerian Path and Eulerian Circuit - Fleury's algorithm - Visit every edge exactly onceAHamiltonian Cycle - Visit every vertex exactly onceAStrongly Connected Components - Kosaraju's algorithmATravelling Salesman Problem - shortest possible route that visits each city and returns to the origin city
- Uncategorized
An algorithmic paradigm is a generic method or approach which underlies the design of a class of algorithms. It is an abstraction higher than the notion of an algorithm, just as an algorithm is an abstraction higher than a computer program.
- Brute Force - look at all the possibilities and selects the best solution
AMaximum SubarrayATravelling Salesman Problem - shortest possible route that visits each city and returns to the origin city
- Greedy - choose the best option at the current time, without any consideration for the future
AUnbound Knapsack ProblemADijkstra Algorithm - finding shortest path to all graph verticesAPrim’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graphAKruskal’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graph
- Divide and Conquer - divide the problem into smaller parts and then solve those parts
BBinary SearchBTower of HanoiBEuclidean Algorithm - calculate the Greatest Common Divisor (GCD)APermutations (with and without repetitions)ACombinations (with and without repetitions)BMerge SortBQuicksortBTree Depth-First Search (DFS)BGraph Depth-First Search (DFS)
- Dynamic Programming - build up a solution using previously found sub-solutions
BFibonacci NumberALevenshtein Distance - minimum edit distance between two sequencesALongest Common Subsequence (LCS)ALongest Common SubstringALongest Increasing subsequenceAShortest Common SupersequenceA0/1 Knapsack ProblemAInteger PartitionAMaximum SubarrayABellman-Ford Algorithm - finding shortest path to all graph vertices
- Backtracking - similarly to brute force, try to generate all possible solutions, but each time you generate next solution you test
if it satisfies all conditions, and only then continue generating subsequent solutions. Otherwise, backtrack, and go on a
different path of finding a solution. Normally the DFS traversal of state-space is being used.
AHamiltonian Cycle - Visit every vertex exactly onceAN-Queens ProblemAKnight's Tour
- Branch & Bound - remember the lowest-cost solution found at each stage of the backtracking search, and use the cost of the lowest-cost solution found so far as a lower bound on the cost of a least-cost solution to the problem, in order to discard partial solutions with costs larger than the lowest-cost solution found so far. Normally BFS traversal in combination with DFS traversal of state-space tree is being used.
Install all dependencies
npm install
Run all tests
npm test
Run tests by name
npm test -- -t 'LinkedList'
Playground
You may play with data-structures and algorithms in ./src/playground/playground.js file and write
tests for it in ./src/playground/__test__/playground.test.js.
Then just simply run the following command to test if your playground code works as expected:
npm test -- -t 'playground'
▶ Data Structures and Algorithms on YouTube
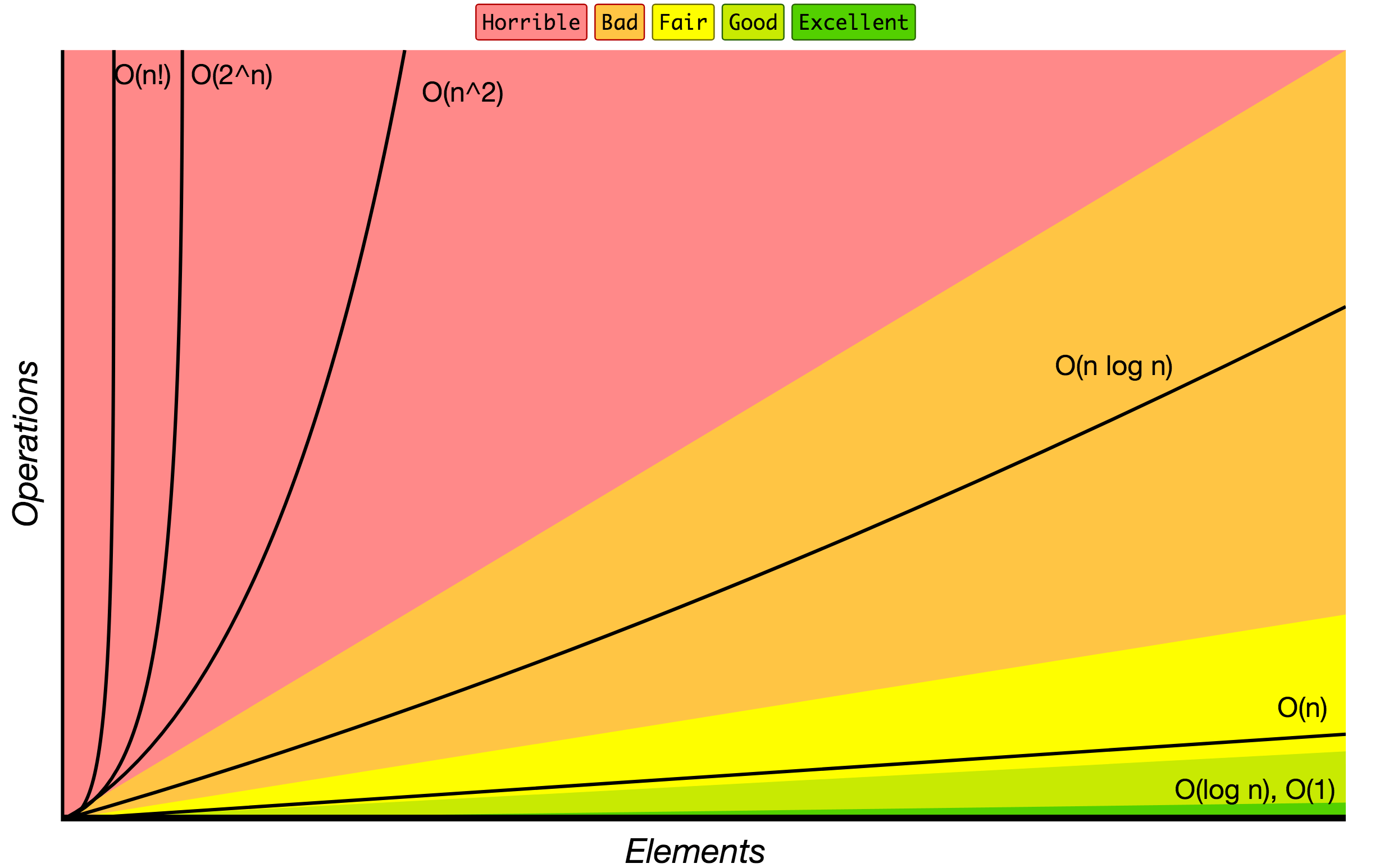
Order of growth of algorithms specified in Big O notation.
Source: Big O Cheat Sheet.
Below is the list of some of the most used Big O notations and their performance comparisons against different sizes of the input data.
| Big O Notation | Computations for 10 elements | Computations for 100 elements | Computations for 1000 elements |
|---|---|---|---|
| O(1) | 1 | 1 | 1 |
| O(log N) | 3 | 6 | 9 |
| O(N) | 10 | 100 | 1000 |
| O(N log N) | 30 | 600 | 9000 |
| O(N^2) | 100 | 10000 | 1000000 |
| O(2^N) | 1024 | 1.26e+29 | 1.07e+301 |
| O(N!) | 3628800 | 9.3e+157 | 4.02e+2567 |
| Data Structure | Access | Search | Insertion | Deletion | Comments |
|---|---|---|---|---|---|
| Array | 1 | n | n | n | |
| Stack | n | n | 1 | 1 | |
| Queue | n | n | 1 | 1 | |
| Linked List | n | n | 1 | 1 | |
| Hash Table | - | n | n | n | In case of perfect hash function costs would be O(1) |
| Binary Search Tree | n | n | n | n | In case of balanced tree costs would be O(log(n)) |
| B-Tree | log(n) | log(n) | log(n) | log(n) | |
| Red-Black Tree | log(n) | log(n) | log(n) | log(n) | |
| AVL Tree | log(n) | log(n) | log(n) | log(n) |
| Name | Best | Average | Worst | Memory | Stable | Comments |
|---|---|---|---|---|---|---|
| Bubble sort | n | n^2 | n^2 | 1 | Yes | |
| Insertion sort | n | n^2 | n^2 | 1 | Yes | |
| Selection sort | n^2 | n^2 | n^2 | 1 | No | |
| Heap sort | n log(n) | n log(n) | n log(n) | 1 | No | |
| Merge sort | n log(n) | n log(n) | n log(n) | n | Yes | |
| Quick sort | n log(n) | n log(n) | n^2 | log(n) | No | |
| Shell sort | n log(n) | depends on gap sequence | n (log(n))^2 | 1 | No | |
| Counting sort | n + r | n + r | n + r | n + r | Yes | r - biggest number in array |
| Radix sort | n * k | n * k | n * k | n + k | Yes | k - length of longest key |