Variational Homoencoder

This is a simple PyTorch implementation for training a Variational Homoencoder, as in the paper:
The Variational Homoencoder: Learning to learn high capacity generative models from few examples

Watch the oral presentation here (UAI 2018)

This code is written to be generic, so it should apply easily to different domains and network architectures. It also extends easily to a variety of generative model structures, including the hierarchical and factorial latent variable models shown in the paper. The code covers the stochastic subsampling of data used during training (Algorithm 1), as well as the reweighting of KL terms in the training objective.

Thanks to pixel-cnn-pp for the PyTorch PixelCNN++ implementation used in example_pixelcnn.py

Feel free to email me at lbh@mit.edu with any questions

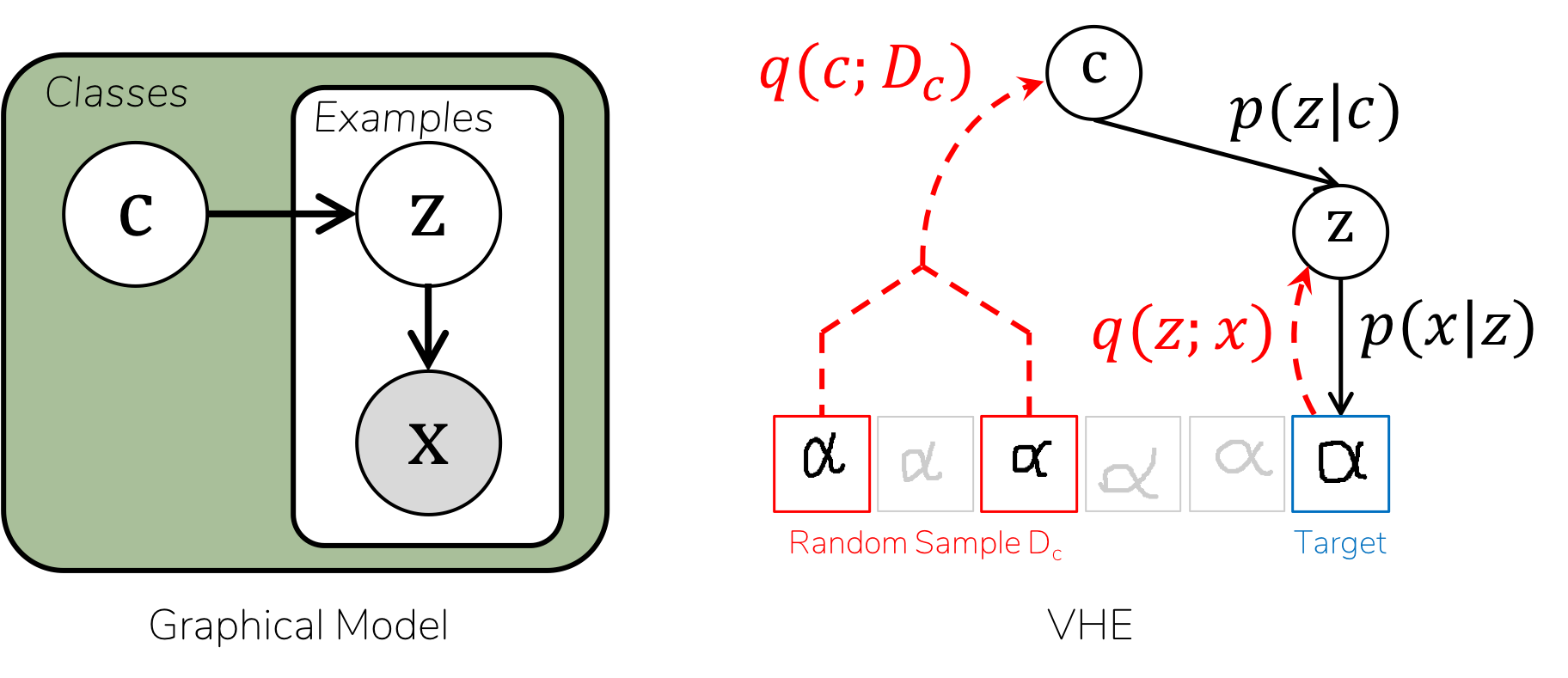
Variational Homoencoder for class-structured datasets

PixelCNN model

example_pixelcnn.py trains a Variational Homoencoder on omniglot using a hierarchical pixelcnn architecture:

How to use

example_czx.py provides a toy example of a model where data are partitioned into classes.

Each class will get its own latent variable c, with a Gaussian prior
Each element will get its own latent variable z, with a Gaussian prior
The likelihood p(x|c,z) will be a Gaussian distribution, with parameters given by a linear neural network.
Encoders are q(z|x) and q(c|D) are both linear

Step 1.

Define every distribution (encoders, decoders, prior) as an nn.Module which implements:

def forward(self, [inputs,] *args, <variable>=None)

Arguments:

First argument is inputs for an encoder (batch * |D| * ...)
<variable> is the random variable to be scored/sampled by the distribution
args are latent variables on which <variable> depends

Returns:

A tuple: (value, log_prob)
If <variable> is None: sample value
Otherwise: value = <variable>

import torch
from vhe import VHE, DataLoader

class Px(nn.Module): # p(x|c,z)
    def __init__(self):
        super().__init__()
        ... #Define any params

    def forward(self, c, z, x=None):
        mu, sigma = ...
        dist = torch.distributions.normal.Normal(mu, sigma) 
        
        if x is None: x = dist.rsample() # Sample x if not given
        log_prob = dist.log_prob(x).sum(dim=1) # Should be a 1D vector with nBatch elements
        return x, log_prob

class Qc(nn.Module): # q(c|D)
    def __init__(self): ...

    def forward(self, inputs, c=None):    
        # inputs is a (batch * |D| * ...) size tensor, containing the support set D
        ...
        return c, log_prob

class Qz(nn.Module): # q(z|x,c)
    def __init__(self): ...

    def forward(self, inputs, c, z=None):
        # inputs is a (batch * 1 * ...) size tensor, containing the input example x
        ...
        return z, log_prob

Step 2.

Create a VHE module from the encoder and decoder modules. All variables use an isotroptic Gaussian prior by default, but may also be specified.

model = VHE(encoder=[Qc(), Qz()], decoder=Px()) #Use default prior c,z ~ N(0, 1)
# or: model = VHE(encoder=[Qc(), Qz()], decoder=Px(), prior=...)

Step 3.

Create a DataLoader to sample data for training.

data_loader = DataLoader(data=data,
        labels={"c":class_labels, # The class label for each element in data
                "z":range(len(data))},  # A unique label for each element in data
        k_shot={"c":5, "z":1}, # Number of elements given to each encoder
        batch_size=batch_size)

Step 4.

Train using the variational lower bound model.score(...)

optimiser = optim.Adam(vhe.parameters(), lr=1e-3)
for epoch in range(...):
    for batch in data_loader:
        optimiser.zero_grad()
        log_prob = model.score(inputs=batch.inputs, sizes=batch.sizes, x=batch.target)
        (-log_prob).backward() # Negative to get loss
        optimiser.step()

vitchyr/vhe