Phased LSTM implementation in Tensorflow

Welcome to the Tensorflow implementation of the recently introduced Phased LSTM by Neil et. al @ NIPS 2016

You can find here the original implementation from Daniel Neil (in Theano)

Results

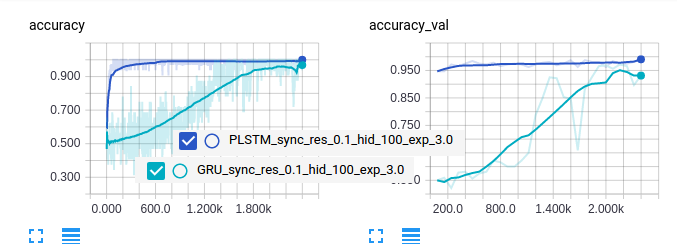
Here is the results of frequency discrimination at high resolution sampling (described in the paper): in dark blue you see PLSTM that converges way faster then GRU (in light blue)

Implementation

Here I implemented the PLSTM in a plug-and-play fashion such that if you wanna use it in one of your models you can switch from LSTMCell/GRUCell to PhasedLSTMCell.

The core of the PLSTM is

    tau = vs.get_variable(
        "T", shape=[self._num_units],
        initializer=random_exp_initializer(0, self.tau_init), dtype=dtype)

    r_on = vs.get_variable(
        "R", shape=[self._num_units],
        initializer=init_ops.constant_initializer(self.r_on_init), dtype=dtype)

    s = vs.get_variable(
        "S", shape=[self._num_units],
        initializer=init_ops.random_uniform_initializer(0., tau.initialized_value()), dtype=dtype)
        # for backward compatibility (v < 0.12.0) use the following line instead of the above
        # initializer = init_ops.random_uniform_initializer(0., tau), dtype = dtype)

    tau_broadcast = tf.expand_dims(tau, dim=0)
    r_on_broadcast = tf.expand_dims(r_on, dim=0)
    s_broadcast = tf.expand_dims(s, dim=0)

    r_on_broadcast = tf.abs(r_on_broadcast)
    tau_broadcast = tf.abs(tau_broadcast)
    times = tf.tile(times, [1, self._num_units])

    # calculate kronos gate
    phi = tf.div(tf.mod(tf.mod(times - s_broadcast, tau_broadcast) + tau_broadcast, tau_broadcast),
                 tau_broadcast)
    is_up = tf.less(phi, (r_on_broadcast * 0.5))
    is_down = tf.logical_and(tf.less(phi, r_on_broadcast), tf.logical_not(is_up))

    k = tf.select(is_up, phi / (r_on_broadcast * 0.5),
                  tf.select(is_down, 2. - 2. * (phi / r_on_broadcast), self.alpha * phi))

then the kronos gate is applied to the cell simply by

        c = k * c + (1. - k) * c_prev
        m = k * m + (1. - k) * m_prev

PhasedLSTMCell has the same parameters set has the LSTMCell plus, here I report the default parameters (as indicated by the paper)

The slope in the off period of the gate

   alpha=0.001

The initial value of r_on

        r_on_init=0.05

The parameter for the initial sampling of tau

        tau_init=6.

tau is sampled as ~exp(uniform(0, tau_init))

Notes for backward compatibility (v < 0.12.0)

The current implementation uses Tensorflow 0.12.0. If you don't wanna update Tensorflow (BTW you should :)) I inserted in the code some commented lines to be backward compatible.

In PLSTM

    initializer=init_ops.random_uniform_initializer(0., tau.initialized_value()), dtype=dtype)
    # for backward compatibility (v < 0.12.0) use the following line instead of the above
    # initializer = init_ops.random_uniform_initializer(0., tau), dtype = dtype)

In the unit test

    sess.run(init)
    # for backward compatibility (v < 0.12.0) use the following line instead of the above
    # initialize_all_variables(sess)

Remember also to change the summaries calls, that is:

    tf.summary.scalar -> tf.scalar_summary 
    tf.summary.histogram -> tf.histogram_summary 
    tf.summary.FileWriter -> tf.train.SummaryWriter 
    tf.summary.merge -> tf.merge_summary

Paper's Task

I implemented the first task described in the paper, that is frequency discrimination. The network is presented with sine waves and has to discriminate between waves of a target range of frequencies (e.g. 5-6 Hz) and waves outside of this range. Furthermore there are three different ways in which you can sample these sine waves:

Low resolution (1 ms)
High resolution (0.1 ms)
Asynchronously

The 3 ways are implemented and you can select them with the flags.

Update 20-12-2016

Added a builder for multilayer PLSM

    outputs = multiPLSTM(_X, lens, n_layers, n_hidden, n_input)

Contact

Let me know if you encounter any problem: enea.ceolini@gmail.com

+Enea