BerTSP

Formulating Neural Sentence Ordering as the Asymmetric Traveling Salesman Problem (INLG'21)

Authors: Vishal Keswani and Harsh Jhamtani

This repository describes the code for our work on Neural Sentence Ordering as ATSP presented at the 14th International Conference on Natural Language Generation.

Abstract [PDF]

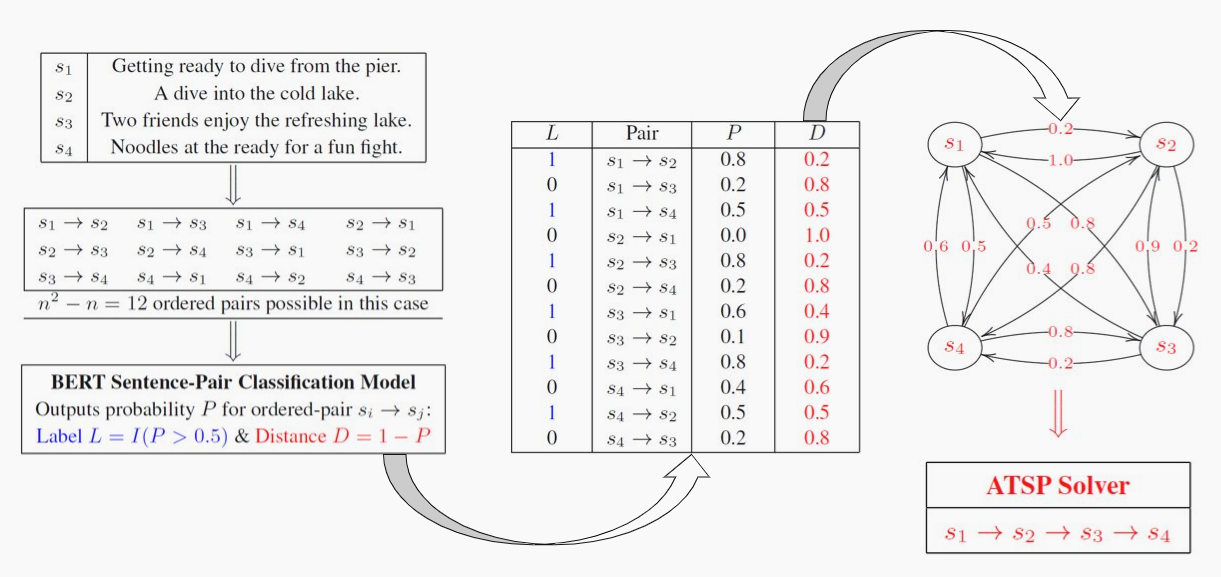
The task of Sentence Ordering refers to rearranging a set of given sentences in a coherent ordering. Prior work (Prabhumoye et al., 2020) models this as an optimal graph traversal (with sentences as nodes, and edges as local constraints) using topological sorting. However, such an approach has major limitations – it cannot handle the presence of cycles in the resulting graphs and considers only the binary presence/absence of edges rather than a more granular score. In this work, we propose an alternate formulation of this task as a classic combinatorial optimization problem popular as the Traveling Salesman Problem (or TSP in short). Compared to the previous approach of using topological sorting, our proposed technique gracefully handles the presence of cycles and is more expressive since it takes into account real-valued constraint/edge scores rather than just the presence/absence of edges. Our experiments demonstrate improved handling of such cyclic cases in resulting graphs. Additionally, we highlight how model accuracy can be sensitive to the ordering of input sentences when using such graphsbased formulations. Finally, we note that our approach requires only lightweight fine-tuning of a classification layer built on pre-trained BERT sentence encoder to identify local relationships.

Datasets

SIND (only SIS is relevant): https://visionandlanguage.net/VIST/dataset.html
NIPS, AAN, NSF abstracts: https://ojs.aaai.org/index.php/AAAI/article/view/11997

Requirements

This code works with the latest versions (8/21).

python
torch
transformers
tensorboardX

Code

Given a set of unordered sentences, we calculate the probability of each 'ordered' sentence-pair using BertForSequenceClassification. We construct a matrix with these probabilities which serves as input for the Traveling Salesman Problem. Since sentence A followed by sentence B has a different input representation than sentence B followed by sentence A, the matrix is asymmetric. We then solve the ATSP via exact and heuristic methods.

The code is based on this repo by @shrimai.
The trained BERT models for calculating sentence-pair probabilities are also available in this repo.

1. Directory structure used

2. Data preparation

Prepare data for training, development and testing:

python prepare_data_modified.py --data_dir ../sis/ --out_dir ../sind_data/ --task_name sind

python prepare_data_modified.py --data_dir ../nips/ --out_dir ../nips_data/ --task_name nips

Output: train.tsv, dev.tsv,test_TopoSort.tsv, test_TSP.tsv

When using trained models, prepare data for testing only:

python prepare_data_modified.py --data_dir ../nips/ --out_dir ../nips_data/ --task_name nips --test_only

Output: test_TopoSort.tsv, test_TSP.tsv

3. Training the sentence-pair classifier

Training custom models:

mkdir ../sind_bert

python model_modified.py --data_dir ../sind_data/ --output_dir ../sind_bert/ --do_train --do_eval --per_gpu_eval_batch_size 16

Output: checkpoint-2000, checkpoint-4000, etc

4. Inference from the sentence-pair classifier

Running inference using trained models:

python model_modified.py --data_dir ../sind_data/ --output_dir ../sind_bert/ --do_test --per_gpu_eval_batch_size 16

Output: test_results_TopoSort.tsv, test_results_TSP.tsv

Running inference using custom trained models:

python model_modified.py --data_dir ../sind_data/ --output_dir ../sind_bert/checkpoint-X/ --do_test --per_gpu_eval_batch_size 16

Output: test_results_TopoSort.tsv, test_results_TSP.tsv

5. Decoding the order via graph traversal

Parameters:

file_path: (required) path to input data directory
decoder: (default - TopoSort) TopoSort/TSP
indexing: (default - reverse) correct/reverse/shuffled
subset: (default - all) cyclic/non_cyclic/all
tsp_solver: (default - approx) approx/ensemble/exact
exact_upto: (default - 8) if exact or ensemble is chosen, upto how many sentences (or sequence length) should exact tsp be used, recommended upto 8 in general (upto 10 for small datasets)

Examples:

python graph_decoder.py --file_path ../nips_data/

python graph_decoder.py --file_path ../nips_data/ --decoder TSP

python graph_decoder.py --file_path ../nips_data/ --decoder TSP --indexing reverse --subset cyclic --tsp_solver ensemble --exact_upto 6

BibTeX

Use the following to cite the paper or code.

@inproceedings{keswani-jhamtani-2021-formulating,
    title = "Formulating Neural Sentence Ordering as the Asymmetric Traveling Salesman Problem",
    author = "Keswani, Vishal  and
      Jhamtani, Harsh",
    booktitle = "Proceedings of the 14th International Conference on Natural Language Generation",
    month = aug,
    year = "2021",
    address = "Aberdeen, Scotland, UK",
    publisher = "Association for Computational Linguistics",
    url = "https://aclanthology.org/2021.inlg-1.13",
    pages = "128--139",
    abstract = "The task of Sentence Ordering refers to rearranging a set of given sentences in a coherent ordering. Prior work (Prabhumoye et al., 2020) models this as an optimal graph traversal (with sentences as nodes, and edges as local constraints) using topological sorting. However, such an approach has major limitations {--} it cannot handle the presence of cycles in the resulting graphs and considers only the binary presence/absence of edges rather than a more granular score. In this work, we propose an alternate formulation of this task as a classic combinatorial optimization problem popular as the Traveling Salesman Problem (or TSP in short). Compared to the previous approach of using topological sorting, our proposed technique gracefully handles the presence of cycles and is more expressive since it takes into account real-valued constraint/edge scores rather than just the presence/absence of edges. Our experiments demonstrate improved handling of such cyclic cases in resulting graphs. Additionally, we highlight how model accuracy can be sensitive to the ordering of input sentences when using such graphs-based formulations. Finally, we note that our approach requires only lightweight fine-tuning of a classification layer built on pretrained BERT sentence encoder to identify local relationships.",
}

vkeswani/BerTSP