___ ___
/ /\ / /\
/ /::\ / /:/
/ /:/\:\ / /:/
/ /::\ \:\ / /::\____
/__/:/\:\_\:| /__/:/\:::::\
\ \:\ \:\/:/ \__\/~|:|~~~~ ___ ___ ___
\ \:\_\::/ | |:| ___ / /\ / /\ / /\
\ \:\/:/ | |:| /__/\ / /::\ / /::\ / /::\
\__\::/ |__|:| \ \:\ / /:/\:\ / /:/\:\ / /:/\:\
~~ \__\| \__\:\ / /::\ \:\ / /::\ \:\ / /::\ \:\
/ /::\ /__/:/\:\_\:\ /__/:/\:\ \:\ /__/:/\:\ \:\
/ /:/\:\ \__\/~|::\/:/ \ \:\ \:\_\/ \ \:\ \:\_\/
/ /:/__\/ | |:|::/ \ \:\ \:\ \ \:\ \:\
/__/:/ | |:|\/ \ \:\_\/ \ \:\_\/
\__\/ |__|:|~ \ \:\ \ \:\
\__\| \__\/ \__\/
This program implements a derivative of BK-Tree data structure described in "Some Approaches to Best-Match File Searching" paper of W. A. Burkhard and R. M. Keller. For more information about the paper, see
@article{362025,
author = {W. A. Burkhard and R. M. Keller},
title = {Some approaches to best-match file searching},
journal = {Commun. ACM},
volume = {16},
number = {4},
year = {1973},
issn = {0001-0782},
pages = {230--236},
doi = {http://doi.acm.org/10.1145/362003.362025},
publisher = {ACM},
address = {New York, NY, USA},
}
In the implementation, I have used below structure to store values in the nodes:
struct node {
distance: Metric distance between current node and its parent.
value : Value stored in current node.
nodes : Nodes collected under this node.
}
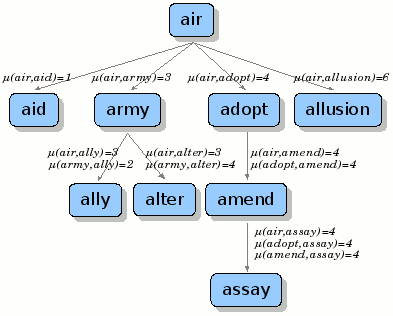
See below figure for an example.
During every search phase, instead of walking through nodes via
j = {j, j+1, j-1, j+2, j-2, ...}
= {0, (-1)^i+1 * ceil(i/2)}, i = 1, 2, 3, ...
as described in the original paper, program sorts nodes according their relative distance to value being searched:
distance = d(searched-value, current-node-value)
sort(nodes, lambda(node) { abs(distance - distance-of(node)) }
There is no restriction on the type of the value which will be stored in the tree, as long as you supply appropriate metric function.
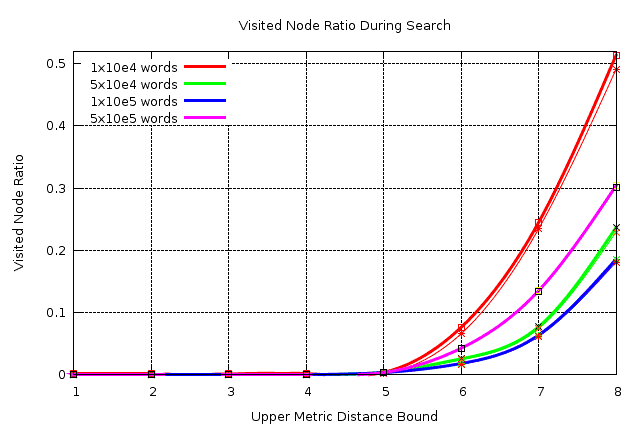
Here is the results of a detailed test performed using BK-TREE package.
In every test, 100 random words are searched in the randomly created word databases. Words stored in the database are varying from 5 characters upto 10 characters.
| DB Size (words) | Threshold (distance) | Scanned Node % | Found Node % |
|---|---|---|---|
| 10,000 | 1 | 0.110 | 0.0100 |
| 2 | 0.110 | 0.0100 | |
| 3 | 0.110 | 0.0100 | |
| 4 | 0.160 | 0.0300 | |
| 5 | 0.370 | 0.1100 | |
| 6 | 7.600 | 6.5800 | |
| 7 | 24.460 | 23.4300 | |
| 8 | 51.360 | 49.0900 | |
| 50,000 | 1 | 0.0022 | 0.0020 |
| 2 | 0.0023 | 0.0021 | |
| 3 | 0.0251 | 0.0030 | |
| 4 | 0.0408 | 0.0127 | |
| 5 | 0.3943 | 0.3196 | |
| 6 | 2.5430 | 2.3869 | |
| 7 | 7.6876 | 7.3874 | |
| 8 | 23.6635 | 22.9339 | |
| 100,000 | 1 | 0.0012 | 0.0010 |
| 2 | 0.0012 | 0.0011 | |
| 3 | 0.0013 | 0.0017 | |
| 4 | 0.0231 | 0.0085 | |
| 5 | 0.3383 | 0.2998 | |
| 6 | 1.7957 | 1.7079 | |
| 7 | 6.3571 | 6.1654 | |
| 8 | 18.5599 | 18.0996 | |
| 500,000 | 1 | 0.0027 | 0.0002 |
| 2 | 0.0029 | 0.0002 | |
| 3 | 0.0039 | 0.0011 | |
| 4 | 0.0012 | 0.0081 | |
| 5 | 0.3444 | 0.3213 | |
| 6 | 0.4244 | 0.4201 | |
| 7 | 13.4834 | 13.3619 | |
| 8 | 30.3728 | 30.1665 |
How this table should be interpreted? The lower the difference between the third and fourth columns, the less redundant node visit performed. And the stability of this difference (which means no fluctuations in the difference) indicates the stability of the convergence.
Here is the graph of above results.
Here is an example about how to used supplied interface.
(defpackage :bk-tree-test (:use :cl :bk-tree))
(in-package :bk-tree-test)
(defvar *words* nil)
(defvar *tree* (make-instance 'bk-tree))
;; Build *WORDS* list.
(with-open-file (in "/home/vy/lisp/english-words.txt")
(loop for line = (read-line in nil nil)
while line
do (push
(string-trim '(#\space #\tab #\cr #\lf) line)
*words*)))
;; Check *WORDS*.
(if (endp *words*)
(error "*WORDS* is empty!"))
;; Fill the *TREE*.
(mapc
(lambda (word)
(handler-case (insert-value word *tree*)
(duplicate-value (ctx)
(format t "Duplicated: ~a~%" (value-of ctx)))))
*words*)
;; Let's see that green tree.
(print-tree *tree*)
;; Test BK-Tree.
(time
(mapc
(lambda (result)
(format t "~a ~a~%" (distance-of result) (value-of result)))
(search-value "kernel" *tree* :threshold 2)))
;; Test brute levenshtein.
(time
(loop with target-word = "kernel"
with results = (sort
(mapcar
(lambda (word)
(cons (levenshtein target-word word) word))
*words*)
#'<
:key #'car)
repeat 50
for (distance . value) in results
while (<= distance 2)
do (format t "~a ~a~%" distance value)))For performance reasons, LEVENSHTEIN function coming with the package has some limitations both on the input string and penalty costs.
(deftype levenshtein-cost ()
"Available penalty costs."
'(integer 0 7))
(deftype levenshtein-input-length ()
"Maximum distance a comparison can result."
`(integer 0 ,(- most-positive-fixnum 7)))Just in case, configure these variables suitable to your needs.