walkingalchemy/calculating-distance-data-science-pilot

Calculating distance

Learning Objectives

• Understand how to use the pythagorean theorem to calculate the distance between two points
• Become familiar with terminology like right angle, hypotenuse, and inverses

Introduction

Previously, we used visualizations to see the closest customers to our salesperson, Bob. Now using a simple graph works fine when Molly only has one salesperson. However, as the business grows to have more salespeople, or when it becomes more difficult to just see who is further away, we need a more formalized approach. So let's attempt to calculate the distance between Bob and a customer.

Once again, here are the locations of Bob and our customers:

Name	Avenue #	Block #
Bob	4	8
Suzie	1	11
Fred	5	8
Edgar	6	13
Steven	3	6
Natalie	5	4

And here are these locations in the form of a scatter plot.

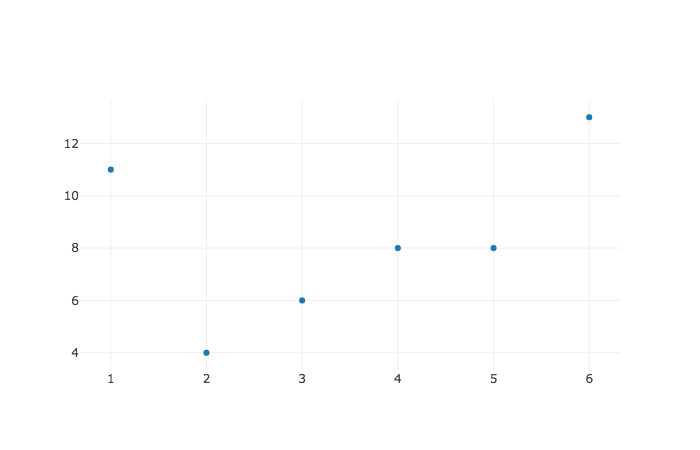
Now, there are no labels in this particular plot, but we should be able to make sense of it anyway. Our table says that Bob is located at avenue 4 and block 8, and when we look at where the x-axis reaches 4 and the y-axis reaches 8, we see a marker right there - that's Bob.

Now our next task is to calculate the distance between Bob, at $(4, 8)$ and a specific customer, the customer at $(3, 6)$. In the general form, we can layout our problem by saying we want to calculate the distance between $(x_1, y_1)$ and $(x_2, y_2)$. And we can assume we are calculating our distance that avenues and blocks are the same length, so we can just calculate our distance in terms of blocks.

Those numbers at the bottom of $x$ and $y$ are used to say that we are referring to our first $x$ and $y$ values with one point, $(x_1, y_1)$ and our second $x$ and $y$ values of $x_2$ and $y_2$.

Calculating distance

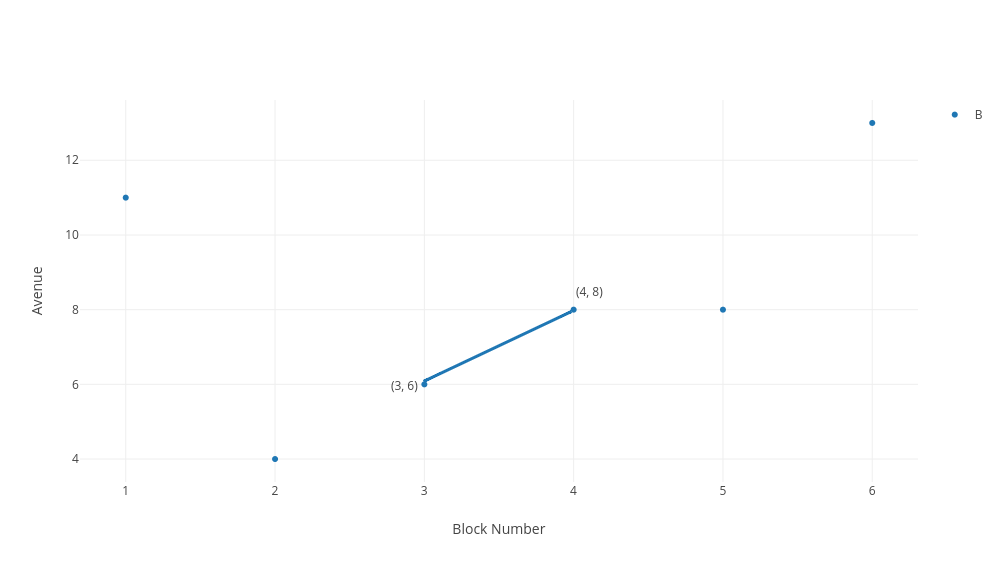
Here's our first approach at calculating distance. To go from our first point of 8th street and 4th avenue to our second point of 6th street and 3rd avenue, we simply go two blocks down and one block to the left for a distance of three blocks.

Now that's a good start, but it's not how mathematicians would calculate distance between points. The definition of distance is the length of shortest path between two points. So imagine, if it helps, that we made our deliveries with the help of a drone. So then what is the shortest path one could take from (4, 8) to (3,6)? We won't prove it, but one single straight line between any two points is the shortest path between them. Here, the shortest path between (4,8) and (3, 6) is a straight diagonal line between them.

That blue diagonal line between the two points is the shortest path between the two points. That is, the distance. Now we need to calculate the length of that line.

Bring in the Pythagoros

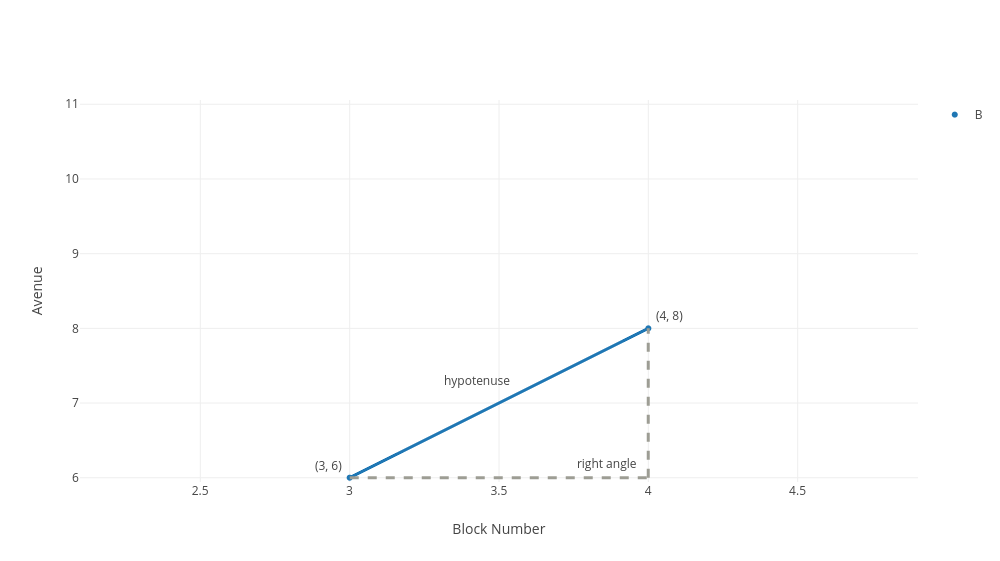
Ok, to calculate that line, we imagine it forms the longest side of a right triangle. With the right triangle spanning horizontally from the lowest x-value to the highest x-value, 3 to 4, and vertically from the lowest y-value to the highest y-value, 6 to 8. Doing this above, you can see we have a nice triangle.

Formally, a right triangle is any triangle where one of the angles is 90 degrees -- also called the right angle. But you can also just know that, if one of the sides is perfectly vertical and the other is perfectly horizontal, then we have a right triangle. What's great about right triangles is that it is easy to calculate the length of the sides of a right triangle. And once we calculate the longest side of the right triangle, we have our distance between the two points.

Ok, this is the formula for calculating the lengths of the sides of a right triangle:

$$ a^2 + b^2 = c^2 $$

Let's break this formula down. In the formula above, $a$ and $b$ are the shorter sides of right triangle -- called the legs -- and $c$ is the longest side of the right triangle -- the **hypotenuse **. So our formula says that the length of the first leg squared plus the length of the second leg square equals the length of the hypotenuse squared.

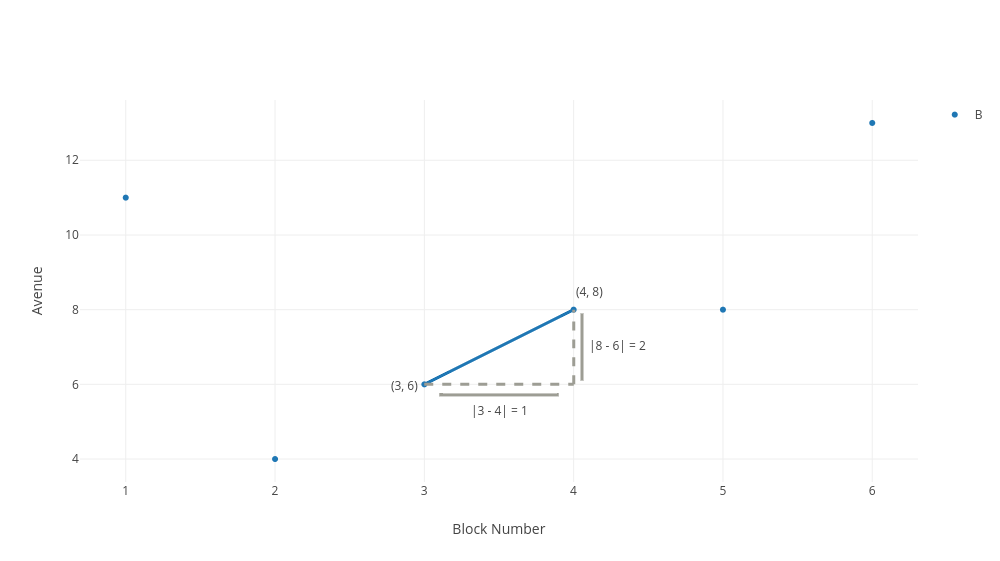
This is great because we already have the information to figure out the length of our two legs, and with that we will have filled in the information needed to find the hypotenuse. We calculate the length of the horizontal side by subtracting our first x-value from our second x-value, then taking the absolute value. We calculate the length of the vertical side by subtracting the first y-value from the second y-value then taking the absolute value.

So in our formula of:

$$ a^2 + b^2 = c^2 $$ we have that: $$a = (x_1 - x_2) = \mid 3 - 4 \mid = 1 $$ $$b = (y_1 - y_2) = \mid 8 - 6 \mid = 2 $$

$$ c^2 = (x_1 - x_2)^2 + (y_1 - y_2)^2 = 1^2 + 2^2 = 5 $$

So simply by plugging in data, we can see that five equals the length of the hypotenuse, squared. And solving for our hypotenuse we have

$c = \sqrt{5}$

Writing $\sqrt{5}$ as a distance is perfectly fine. However, if you would rather see this in decimal form, simply plug the $\sqrt{5}$ into a calculator (or type "sqrt 5" into Google's search bar) and you will get 2.23. So that is the distance between our two points. We have solved it!

Squares, Square Roots, and Inverses

Squares - Squaring something simply means multiplying something by itself. So for example, 5 squared equals 5 $\times$ 5. Four squared equals 4 $\times$ 4. We denote four squared with the a raised number 2, as in $4^2$. The two is the number of times we are multiplying four by itself.

Square Roots - Now we can go from a number's square back to the original square with the square root. For example, the square of 4 is 4 $\times$ 4, which equals 16. And the square root of 16 should undo the operation of squaring, so the square root of 16 equals four, and we denote the square root of 16 as $\sqrt{16}$.

**Inverses ** - In mathematics, we the inverse is anything that undoes the operation. So the inverse of squaring is taking the square root. The inverse of multiplying by ten is dividing by ten. Here is a question:

What is the inverse of putting shoes on?

Well, just think of the definition - inverse means undoing the operation, and the undoing putting shoes on is taking shoes off.

Moving to the general form

Now that we have seen how to solve for length of the hypotenuse in our example above, let's make sure we know how to do this in general. We start with the formula:

$$ a^2 + b^2 = c^2 $$ and putting this formula in terms of our two points, $x$ and $y$, we have : $$ (x_1 - x_2)^2 + (y_1 - y_2)^2 = c^2 $$

and solving for $c$ we have

$c = \sqrt{(x_{2} - x_{1})^2 + (y_{2} - y_{1})^2}$

where c is the length of the hypotenuse, or the distance between our two points.

So, that is the famous Pythagorean Formula, which says that in a right triangle, where $c$ is the length of the hypotenuse, and $a$ and $b$ are the other two sides:

Summary

Ok, that was a lot of math, but it was worth it. We now know that to calculate the distance between any two points we can simply square the differences the between the points's $x$ and $y$ values, sum the squares, and then take the square root of the sum to calculate the distance between two points.

We can do this because a single line is the shortest path between two points, also known as the distance between two points. Because the Pythagorean Theorem gives us a formula $a^2$ + $b^2$ = $c^2$, for calculating the length of a hypotenuse of any right triangle, we simply extend a horizontal line and a vertical line from the two points to form the remaining two sides of a right triangle, and then we calculate the distance by knowing that the square of one side, $a^2$ is $(x_{2} - x_{1})^2$ or the x coordinate of one point minus the x coordinate of the other point squared, and the square of the length of the other side, that is $b^2$, is $(y_{2} - y_{1})^2$, the y coordinate of one point minus the y coordinate of the other point squared. So this gives us $(x_{2} - x_{1})^2$ + $(y_{2} - y_{1})^2$ = $c^2$ or, solving for c, $c = \sqrt{(x_{2} - x_{1})^2 + (y_{2} - y_{1})^2}$.