cc

Chess Challenge.

Find all unique configurations of a set of normal chess pieces on a chess board with dimensions M×N where none of the pieces is in a position to take any of the others. Assume the colour of the piece does not matter, and that there are no pawns among the pieces.

Input

The dimensions of the board: M, N
The number of pieces of each type (King, Queen, Bishop, Rook and Knight) to try and place on the board.

Output

A list of all the unique configurations to the console for which all of the pieces can be placed on the board without threatening each other.

The output is easily machine parsable in the format [number of configurations] comma separated list of the pieces and locations that ends with a semicolon for each solution, positions use common notation e.g. Ra1, Rb2; (the time it took to find the solution).

[2] Ra1, Rb2; Ra2, Rb1; (64.127µs)

Algorithm

The algorithm used is as follows.

Start with an empty board.
Find all cells where the next piece can be placed. First run this is every cell.
For all possible cells, put the piece there and recurse down with the new configuration and find all possible cells.
When there are no new pieces to place the configuration is a solution.
If a piece cannot be placed anywhere go to the next possible solution.

Installation

$ go get github.com/walle/cc/...

Build from source

$ go get github.com/walle/cc/...
$ cd $GOPATH/src/github.com/walle/cc
$ go build -o cc cmd/cc/main.go
$ ./cc -h

Usage

usage: cc --columns COLUMNS --rows ROWS [--kings KINGS] [--queens QUEENS]
[--bishops BISHOPS] [--rooks ROOKS] [--knights KNIGHTS] [--notation NOTATION]
[--ascii]

options:
  --columns COLUMNS, -c COLUMNS
                         the number of columns to use on the board
  --rows ROWS, -r ROWS   the number of rows to use on the board
  --kings KINGS, -k KINGS
                         the number of kings to use on the board
  --queens QUEENS, -q QUEENS
                         the number of queens to use on the board
  --bishops BISHOPS, -b BISHOPS
                         the number of bishops to use on the board
  --rooks ROOKS, -t ROOKS
                         the number of rooks to use on the board
  --knights KNIGHTS, -n KNIGHTS
                         the number of knights to use on the board
  --notation NOTATION    convert notation to visualize a board as ascii
  --ascii                visualize in ascii instead of notation
  --help, -h             display this help and exit

Example usage

$ cc -c 3 -r 3 -k 2 -t 1
[4] Rb1,Ka3,Kc3; Kc1,Ra2,Kc3; Ka1,Rc2,Ka3; Ka1,Kc1,Rb3; (110.17µs)

$ cc -c 3 -r 3 -k 2 -t 1 --ascii
[4]

1
 . R .
 . . .
 K . K

2
 . . K
 R . .
 . . K

3
 K . K
 . . .
 . R .

4
 K . .
 . . R
 K . .

(348.274µs)

$ cc -c 7 -r 7 --notation Kb2,Ke2,Qg3,Na6,Bb6,Bc6,Qf7
 . . . . . . .
 . K . . K . .
 . . . . . . Q
 . . . . . . .
 . . . . . . .
 N B B . . . .
 . . . . . Q .

Testing

Use the go test tool.

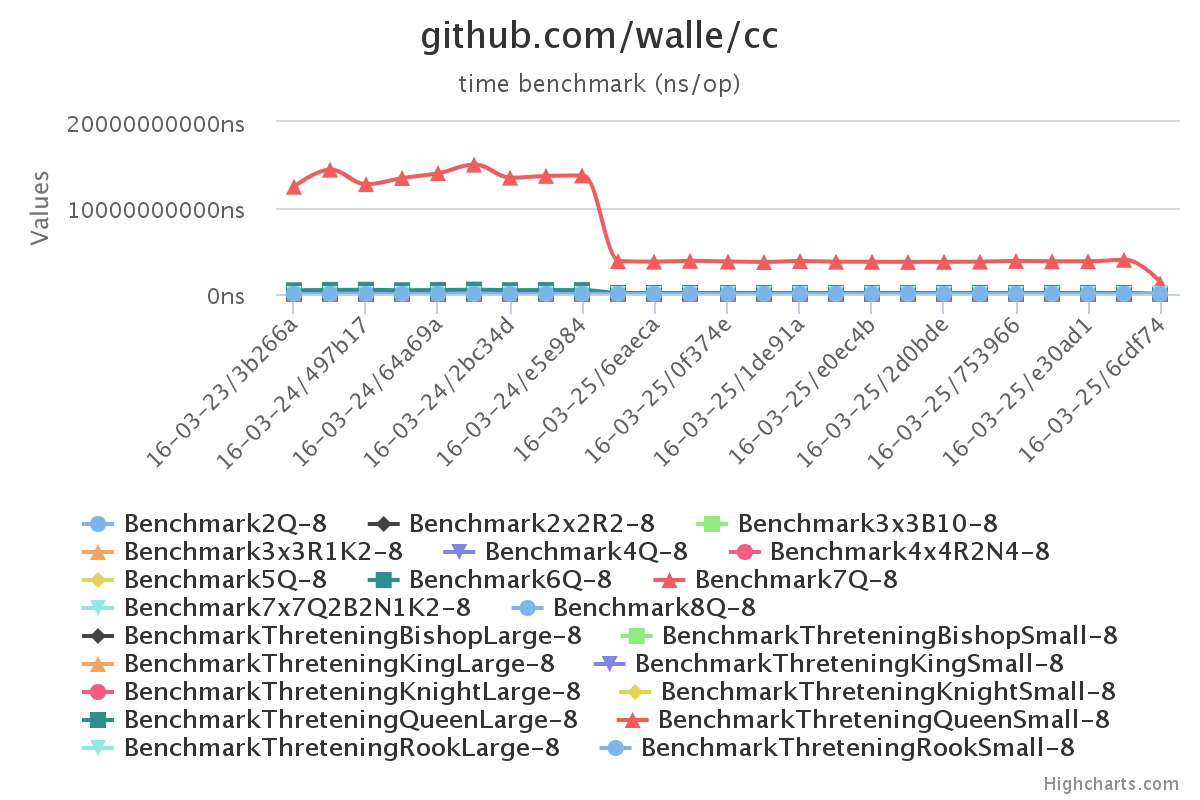
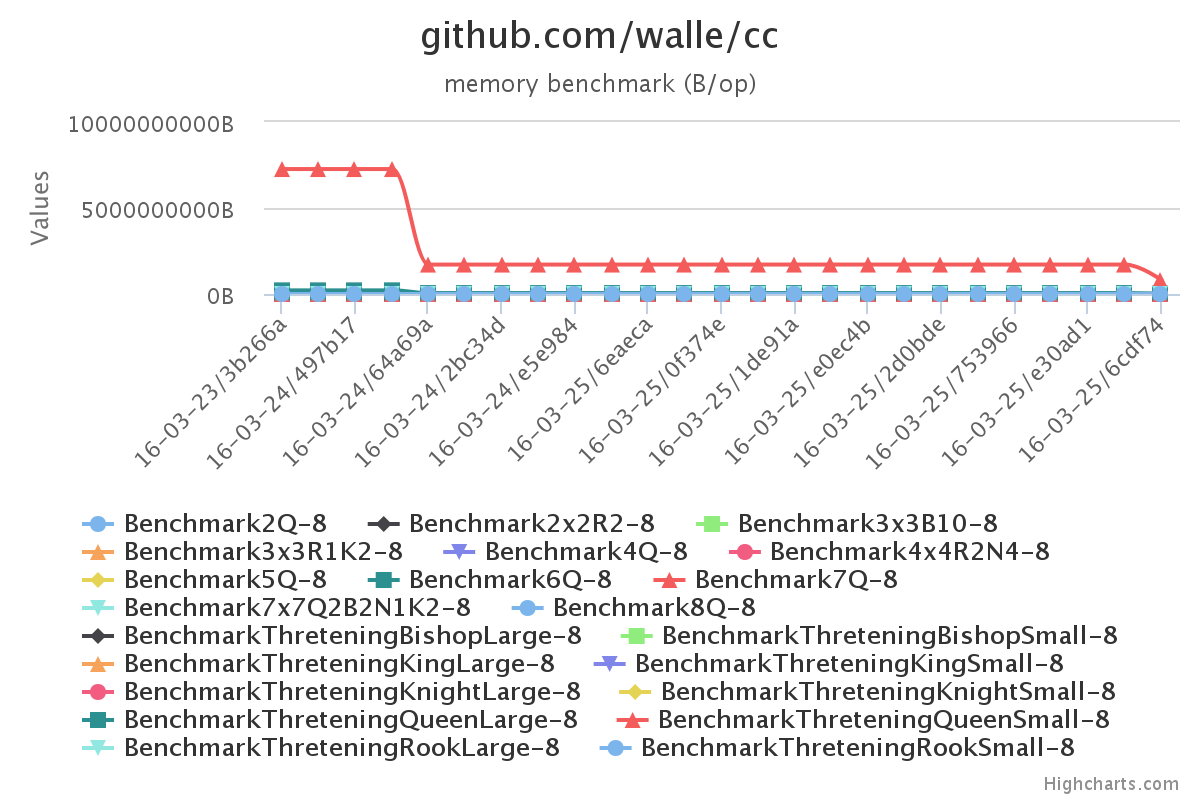
$ go test -cover ./...

$ go test -bench=. -benchmem ./...

Benchmarks

The images are generated using gobenchui https://github.com/divan/gobenchui

Time benchmark

Memory benchmark

Basically three events stand out.

First naive solution, which uses a lot of memory and takes a lot of time.
Changing data structure, time goes up a little but memory usage goes down.
Using channels to run in parallell makes the time go down.

License

The code is under the MIT license. See LICENSE for more information.