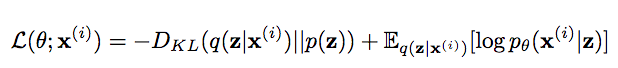Timeseries clustering

Timeseries clustering is an unsupervised learning task aimed to partition unlabeled timeseries objects into homogenous groups/clusters. Timeseries in the same cluster are more similar to each other than timeseries in other clusters

This algorithm is able to:

Identify joint dynamics across the sequences
Eliminate lags (time-shifts) across sequences (usually called lag-invariance)
Generate features which are interpretable.

In general, timeseries clustering algorithms are of two types:

Feature based - transform raw data using feature extraction, run clustering on top of generated features
Raw-data based - directly applied over timeseries vectors without any space-transformations

Variational Recurrent Auto-encoders (VRAE)

VRAE is a feature-based timeseries clustering algorithm, since raw-data based approach suffers from curse of dimensionality and is sensitive to noisy input data. The middle bottleneck layer will serve as the feature representation for the entire input timeseries.

Architecture

The network

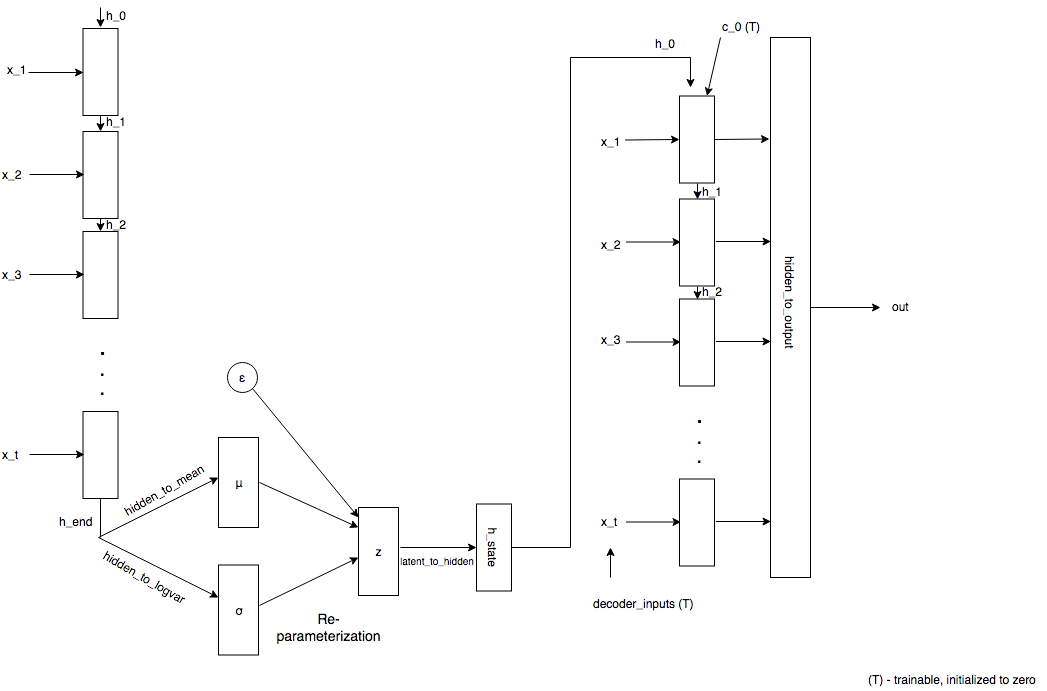
From here on, RNN refers to Recurrent Neural Network architecture, either LSTM/GRU block. Our model comprises mainly of four blocks

The encoder: A sequence of input vectors is fed to the RNN, last hidden layer h_end, is plucked from the RNN and is passed to the next layer
The encoder-to-latent layer: h_end is mapped to the mean and standard deviation by using a linear layer
Given mean and std. deviation, reparameterization is performed during training. This essentially means sampling latent vector from a distribution defined by its mean and std. deviation
The latent-to-decoder layer: Latent vector sampled is passed through a linear layer to obtain initial states for the decoder RNN.
The decoder: Given the initial states of the decoder, decoder inputs are initialized to zero and are updated using backpropagation. Outputs of the decoder and passed on to the output layer
The output layer: This linear layer maps the output of decoder RNN to sequence length to obtain x_decoded

Loss function

The network is jointly trained on 2 loss functions:

KL-divergence between the distribution learned in latent space with the normal distribution.
An auto-encoder learns the identity function, so the sequence of input and output vectors must be similar. In our case, MSE loss is calculated between x_decoded and x forming the reconstruction error. It signifies the extent to which input is reconstructed. Another option : SmoothL1Loss

Optimizer

Given the gradients and the weights, Adam is used to update the weights. Option provided to use Stochastic Gradient Descent(SGD) for optimization.

Why recurrent neural network in an auto-encoder?

The length of timeseries may vary from sample to sample. Conventional techniques only work on inputs of fixed size.
The patterns in timeseries can have arbitrary time span and be non stationary. The recurrent neural network can learn patterns in arbitrary time scale (lag invariance)
The weight/linear layer in vanilla auto-encoders might grow large in size as the length of time series increases, eventually slowing down the learning process.

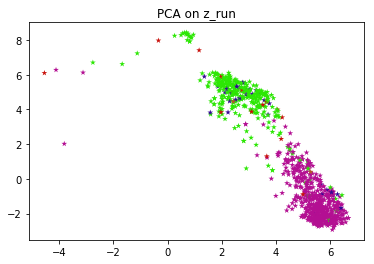
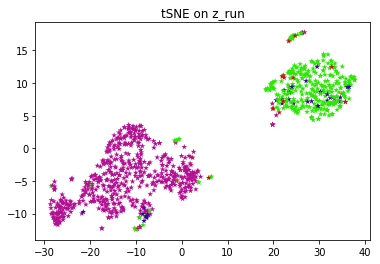
Exploratory data analysis is performed on the latent vectors in order to visualize the clusters formed. Since the dimension of z can be more than 2, it has to be converted to a lower dimension to be visualized. PCA and t-SNE are performed to visualize the clusters.

Example - ECG data

NOTE: Please be wary of using this dataset. I had developed this library for an internal client project and had to obfuscate data using an opensource dataset. You may find some errors in the way I'm using this data. Checkout the FAQs below if you have doubts on the implementation.

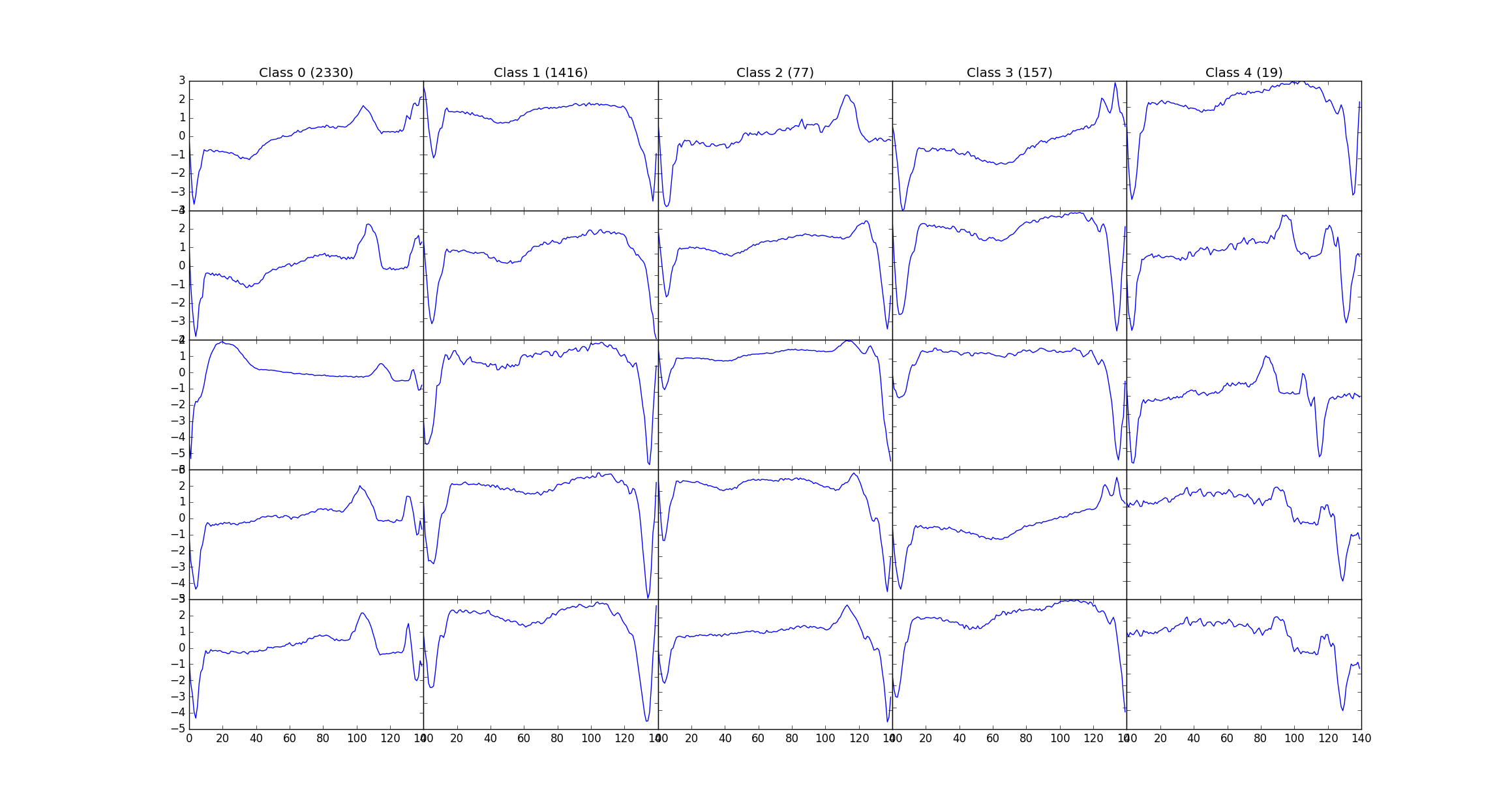
The above network is trained on a dataset of 8500 ECG's and tested on 950 ECG's Named ECG5000 on the UCR archive, this dataset has 5 classes, and the labels are used to generate different colors on PCA, tSNE chart.

Here's a snapshot of the data:

Results

When the VRAE model is run on this set of hyperparameters, we get the plots for both PCA and tSNE. PCA and t-SNE are performed in order to convert to a lower dimension and to visualize the clusters. This figure shows that latent space exhibits structure. The pink and green labels obviously cluster in different parts of the space.

FYI, the entire algorithm is an unsupervised one. Labels are just used to color and visually test the results. If you don't have labels for your application, you can run k-means on top of latent vectors to get labels and use those labels to color individual data points.

FAQs

Does VRAE support multivariate data-sets?
Yes. It does. There's a parameter called number_of_features. In the case of multi-variate timeseries, pass the degree of freedom here. In case of univariate, please pass 1. Refer to this commit - e7b57a6
Does VRAE support unlabelled timeseries data-sets?
Auto-encoders are designed to work on unlabelled data, but you would need a subset of labelled data to justify the generated embeddings. This is similar to the case where you have word vectors, but you can justify those embeddings semantically by seeing if "king - queen", etc.. There has to be a way to know if VRAE is working properly (train set has to have labelled data for this). That said, you don't need labels if you have a way of visualizing the clusters.
Does VRAE support classification as well?
No. VRAE only converts sparse "time-series" to dense vectors. To generate classification on top of it needs the vectors to be passed to some algorithm (k-means in my example)
In the ECG example shown, you show compression from 140 elements to 20 elements. What is an appropriate compression ratio for larger lengths, say 9k?
The number of time-series to be fed isn't a problem, but the dimension of each time-series is. To combat this, I propose 3 approaches as described below

The best, naive solution is to go ahead with the raw clustering and feeding in 9k dimensions. Build a much stronger neural network with "gradually" descending layer in encoders and their relative pairs in the decoders. This network will have a lot of parameters to train and would need larger machine and more time to train this. For example, you can go with 9k - 2048 - 512 - 128 - 32 (encoder) and 32 - 128 - 512 - 2048 (decoder). This way you'll have 32 dimensions in the end.
Use a sliding window approach where you have a window-size of k. Getting this k would need a lot of preprocessing + traditional forecasting + auto-regressive plots.
Average out x-days of stocks and cluster based on them. Obtain this x till the time your current date("dt") stops influencing ("dt-x") values.

Is VRAE a stateful version?
Yes. VRAE makes extensive use of RNN(LSTM/GRU) blocks which themselves are stateful in nature. Vanilla neural networks are stateless. Setting required_grad=False makes a variable act like a constant and including required_grad=True lets the network "learn" the variable's value through backprop.

Application Areas

Anomaly detection
Data reduction
Determining products with similar selling patterns
Product cannibalization
New product introduction
Low selling items
Items that are introduced and phased out quite frequently (can't estimate seasonality, data < 1yr)

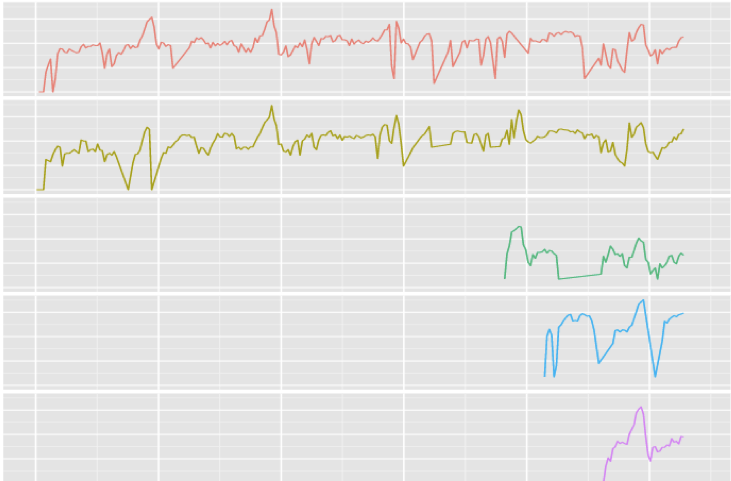
Solution: Forecast items in groups (borrowed from here)

Even though each item has a short/sparse life cycle, clustered group has enough data
Modeling the group as a whole, is more robust to outliers and missing data.

Conclusion

We present variational recurrent auto-encoder that learns the structure in the timeseries. Training is unsupervised. When we color the latent vectors with the actual labels, we show that the structure makes sense.

Requirements

Repo works with:

python==3.5
torch==1.0.0
numpy==1.15.4
plotly==3.4.2
scikit-learn==0.20.1
matplotlib==3.0.2
scipy==1.1.0

wanwanliang/timeseries-clustering-vae