weberBen/Automatic_differentiation

Implementation of automatic differentiation (AD) in forward and backward modes with mathematical explanations

Automatic Differentiation (AD)

Implementation of a simple automatic differentiation (forward mode with dual number and backward mode with NetworkX for the computation graph) with mathematical explanations.

Mathematical explanations

The mathematical backgrounds of the forward and backward modes are explained here

Forward mode

Import packages :

from DualNumber import DualNumber
from MathLib.Functions import sin, cos, tan, log, exp

Define a function $f(x,y)$:

def f(x, y):
    return sin(x)*y + 7*(x*x)

Compute the partial derivative $\frac{\partial{f}}{\partial{x}}$

x = DualNumber(4, 1)
y = DualNumber(7, 0)

res = f(x, y)

f_val = res.primal # f evaluted at (x,y)=(4,7)
df_x = res.tangent # df/dx at (x,y)=(4,7)

Compute the partial derivative $\frac{\partial{f}}{\partial{y}}$

x = DualNumber(4, 0)
y = DualNumber(7, 1)

res = f(x, y)

f_val = res.primal # f evaluted at (x,y)=(4,7)
df_y = res.tangent # df/dy at (x,y)=(4,7)

Compute the directionnal derivative $\nabla_{a}f$ for $a=(0.5,3)$

x = DualNumber(4, 0.5)
y = DualNumber(7, 3)

res = f(x, y)

f_val = res.primal # f evaluted at (x,y)=(4,7)
dir_derivative = res.tangent # directionnal derivative at (x,y)=(4,7) in direction a=(0.5,3)

See more examples here

Backward mode

Import packages :

from ComputationLib.Vector import Vector
from MathLib.Functions import sin, log, tan, exp, cos

Define a function :

def f(x, y):
    return sin(x)*y + 7*(x*x)

Define variables $x=7$, $y=7$

x = Vector(4, requires_grad=True)
y = Vector(7, requires_grad=True)

res = f(x, y)

res.backward()

Get the partial derivatives

dx = x.grad
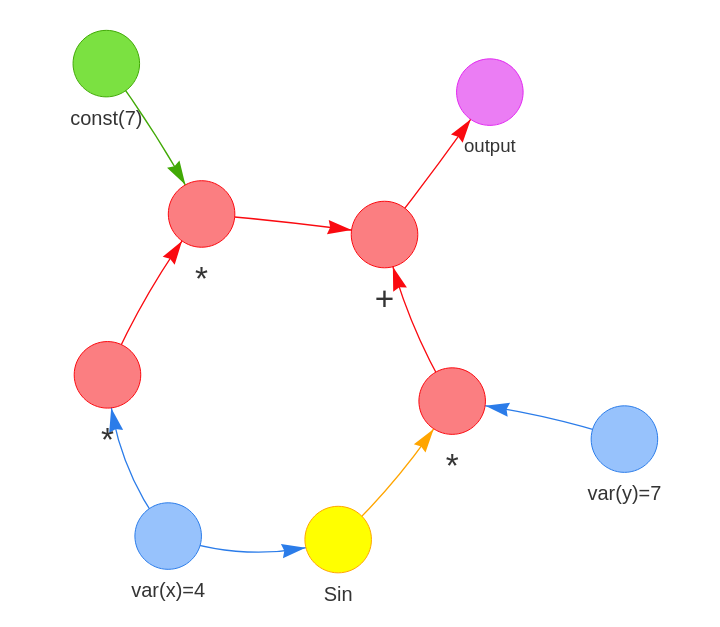
dy = y.grad

You can also display the computation graph :

from ComputationLib.ComputationGraph import ComputationGraphProcessor

cgp = ComputationGraphProcessor(res, human_readable=True)
cgp.draw(display_nodes_value=True)

Self reflective operations (i.e $x^2=x \times x$, $\frac{x}{x}$, $x+x$, $x-x$, ...) are represented as a single edge in the graph.

You can set the label option when declaring new Vector to render the variable name during the graph drawing (i.e: x = Vector(14.23, requires_grad=True, label="x")).

See more examples here

Custom functions

You can define your own functions as follows :

import math
from DualNumber import DualNumber
from MathLib.FunctionWrapper import Function

class MyCos(Function) :
    def __init__(self):
        super().__init__() # needed
    
    def compute(self, input_value):
        if type(input_value) is DualNumber:
            return DualNumber(math.cos(input_value.primal), - input_value.tangent*math.sin(input_value.primal))

        return math.cos(input_value)
    
    def derivative(self, input_value):
        return -math.sin(input_value)

mycos = MyCos().apply()

Then :

mycos(4)

The compute method is used for the forward mode and for computing the value of the function when evaluating it. The derivative is used for the backward mode.

Extending the lib

Scalar field functions

The lib currently accepts only scalar functions, but by using numpy instead of math lib for each function we can now evaluate scalar field functions :

import numpy as np
from DualNumber import DualNumber
from MathLib.FunctionWrapper import Function

class NumpyCos(Function) :
    def __init__(self):
        super().__init__() # needed
    
    def compute(self, input_value):
        if type(input_value) is DualNumber:
            return DualNumber(np.cos(input_value.primal), - input_value.tangent*np.sin(input_value.primal))

        return np.cos(input_value)
    
    def derivative(self, input_value):
        return -np.sin(input_value)

cos = NumpyCos().apply()

See more examples here

Jacobian

The Jacobian of a function $f: (a_1, a_2, ..., a_n) \mapsto (f_1(a_1, ..., a_n), ..., f_m(a_1, ..., a_n))$ from $R^n$ to $R^m$ is not natively implemented but can be computed on each $f_i$ one by one :

def computeJacobianBackward(inputs, func_res):
    number_inputs = len(inputs)
    number_outputs = len(func_res)

    jacobian = np.zeros((number_inputs, number_outputs))

    for index, fi in enumerate(func_res):
        fi.backward()

        for a_index, a in enumerate(inputs):
            jacobian[index][a_index] = a.grad
    
    return jacobian

See more examples here

Installation

cd app
pip install -r requirements.txt

Limitations

Thread safe

Thread safe can be implemented by hardening the access to the computation graph for each vector and probably the uuid generation for vector id. But it's not really the purpose of that lib.